
- •Проектирование кривошипно - ползунного механизма
- •Самарская государственная академия путей сообщения, 2004
- •1. Кинематический синтез механизма
- •Рассмотрим методику синтеза механизмов по этим параметрам.
- •1.2. Синтез центрального механизма по ходу ползуна и
- •Скорость точки в
- •2. Кинематический и кинетостатический анализ кривошипно-ползунного механизма
- •2.1. Кинематический и кинетостатический анализ
- •2.1.1. Определение траекторий движения точек звеньев механизма
- •2.1.3. Кинетостатический анализ механизма
- •2.1.4. Определение уравновешивающего момента
- •2.2. Алгоритм кинематического и кинетостатического анализа с использованием эвм
2.1.4. Определение уравновешивающего момента
методом проф. Н.Е. Жуковского
Вычерчиваем
план скоростей, повернутый вокруг полюса
на угол 900
противоположно угловой скорости
входного звена. В соответствующих точках
прикладываем все силы, приложенные к
звеньям механизма (кроме реакций в
кинематических парах). Момент сил инерции
массы второго звена заменяем парой сил
инерции
![]() и
и![]() ,
приложенных в точкахВ
и С
и направленных так, чтобы направление
вращения под действием пары сил
,
приложенных в точкахВ
и С
и направленных так, чтобы направление
вращения под действием пары сил
![]() было таким же, как и под действием момента
сил инерции
было таким же, как и под действием момента
сил инерции![]() .
.
 =
=![]() =0,9Н.
=0,9Н.
Запишем условие равновесия плана скоростей как жесткого рычага относительно полюса р.
![]() ;
;
![]() .
.
Из этого уравнения находим силу Pур.
![]()
![]() =
=![]() .
.
Вычислим уравновешивающий момент, определяемый по методу проф. Н.Е. Жуковского
![]() 85Н
0,0192м=1,632Нм.
85Н
0,0192м=1,632Нм.
Погрешность определения уравновешивающего момента разными способами:
 %
=
%
=![]() =2,3%
5% .
=2,3%
5% .
Это означает, что результаты расчетов, выполненных разными методами имеют хорошее совпадение.
2.2. Алгоритм кинематического и кинетостатического анализа с использованием эвм
2.2.1. Кинематический анализ
Мгновенное положение звена 2 определяется углом . Для его определения спроектируем звенья 1 и 2 на ось у (рис. 2.1).

Рис. 2.1
r
sin
+ e =
![]() sin (900
-
);
= 1t
;
sin (900
-
);
= 1t
;
откуда
= arccos[(r sin1t
+e)/
![]() ].
].
Угловая скорость шатуна в его относительном вращательном движении
2 = d /dt .
Угловое ускорение шатуна
2 = d 2 / dt = d2 /d t2 .
Скорость ползуна
![]() ,
,
где VB = r 1 - скорость точки В;
VCB
=
![]() 2
- скорость движения точки С относительно
точки В.
2
- скорость движения точки С относительно
точки В.
Найдем проекции этих скоростей на координатные оси:
VCx = VBx + VCBx = - VB sin + VCB cos ;
VСy = V By + VCBy = VB cos + VCB sin .
Т.к. ползун перемещается вдоль направляющей, параллельной оси Х, то VС= VCx , а VСy = 0.
Ускорение точки С
![]() ,
,
где ![]() -
ускорение точкиВ;
-
ускорение точкиВ;
![]() -
нормальная составляющая ускорения
точкиС
в движении относительно точки В;
-
нормальная составляющая ускорения
точкиС
в движении относительно точки В;
![]() -
тангенциальная составляющая ускорения
т.С
в движении относительно точки В.
-
тангенциальная составляющая ускорения
т.С
в движении относительно точки В.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ускорения центров масс звеньев и их проекции на координатные оси:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
2.2.2. Кинетостатический анализ
Определяем силы, действующие на звенья механизма.
Силы тяжести звеньев:
![]() ;
;
![]() ;
;![]() .
.
Силы инерции масс звеньев и их проекции на координатные оси:
![]() ;
;
![]()
![]() ;
;![]() ;
;
![]() ;
;
![]()
![]() ;
;![]() ;
;
![]() .
.
Момент сил инерции масс шатуна, возникающий при его движении:
![]() .
.
Для определения реакций в кинематических парах и уравновешивающего момента рассмотрим условия равновесия структурных групп.
Группа звеньев 2-3 (шатун- ползун)
План нагружения группы 2-3 показан на рис. 2.2.

Рис. 2.2
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
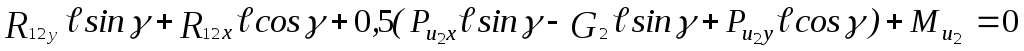 .
.
 ;
;
![]()
![]() ;
;
![]() ;
;
Введем ограничение: в соответствии с определением силы полезного сопротивления сила полезного сопротивления Q действует только во время рабочего хода ползуна, т.е. при Vc >0.
![]() -
реакция в кинематической паре В
(шатун-кривошип).
-
реакция в кинематической паре В
(шатун-кривошип).
Реакция в кинематической паре шатун-ползун
![]() ;
;
![]() ;
;
![]() .
.
Входное звено (кривошип)
![]() .
.
![]() .
.
![]() План
нагружений кривошипа приведен на рис.2.3
План
нагружений кривошипа приведен на рис.2.3

Рис.2.3
![]() ;
;![]() ;
;
![]() ;
; ![]() ;
;
![]() .
. ![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
R41 - реакция в кинематической паре А (стойка-кривошип)
![]() .
.
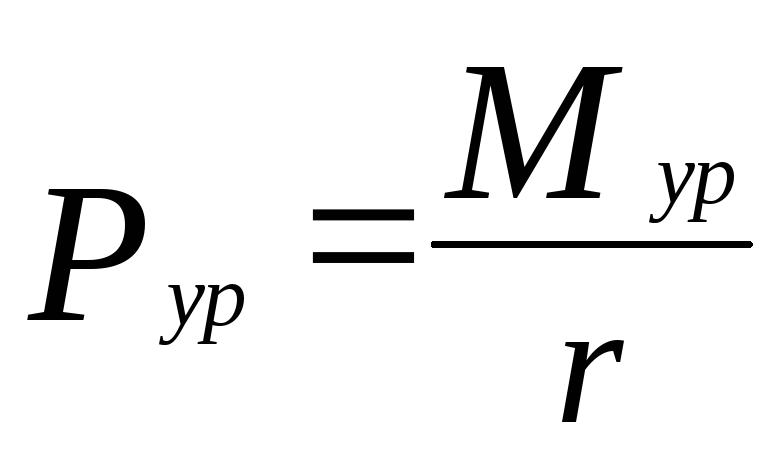 ;
;
![]() ;
;![]() .
.
Определим уравновешивающий
момент методом проф. Н.Е. Жуковского
(![]() ):
):
![]() ,
,
где 1 - угловая скорость кривошипа;
Fi, Mi - силы и моменты сил, действующие на i звено;
Vi - скорость точки приложения i–ой силы;
i - угловая скорость i–го звена;
i - угол между вектором i–й силы и скоростью точки ее приложения;
![]() -
уравновешивающий
момент,приложенный
к кривошипу.
-
уравновешивающий
момент,приложенный
к кривошипу.
Первое слагаемое удобно представить как сумму произведений проекций сил и скоростей точек их приложения на координатные оси. Тогда
 .
.
Рассчитывается погрешность определения уравновешивающего момента из условий равновесия и методом профессора Н.Е. Жуковского
![]() .
.
Для реализации изложенного выше алгоритма кинематического и кинетостатического анализа механизма разработана программа расчета на персональных ЭВМ.
Библиографический список
Теория механизмов и машин./ Под редакцией К.В. Фролова. М.: Высшая школа, 2002. 496 с.
Курсовое проектирование по теории механизмов и машин. Учебное пособие / Под редакцией П.В. Семина, Н.И. Наумкина. Саранск: Изд. Мордовского университета, 2003. 332 с.
Попов А.С. и др. Курсовое проектирование по теории механизмов и механике машин: Учебное пособие для втузов. М.: Высш. шк., 1998. 351 с.


