Министерство образования Республики Беларусь
Учреждение образование «МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРОДОВОЛЬСТВИЯ»
Кафедра информатики и вычислительной техники
РЕШЕНИЕ УРАВНЕНИЙ
ВЭЛЕКТРОННЫХ ТАБЛИЦАХ
ИСИСТЕМАХ КОМПЬЮТЕРНОЙ МАТЕМАТИКИ
Методические указания для студентов специальностей
1-36 09 01 – «Машины и аппараты пищевых производств» 1-36 20 01 – «Низкотемпературная техника»
дневной и заочной формы обучения
Могилев 2010
2
УДК 519.61 Рассмотрено и утверждено на заседании кафедры
«Информатика и вычислительная техника» Протокол № 11 от «» 30.06 2010 г.
Составители: |
старший преподаватель И.П.Овсянникова |
|
зав. кафедрой ИВТ, к.ф.-м.н. Г.Н. Воробьев |
Рецензент |
к.ф.-м.н., доцент В.Л. Титов |
© Могилевский государственный университет продовольствия
3 |
|
|
|
СОДЕРЖАНИЕ |
|
ВВЕДЕНИЕ............................................................................................................................................................................... |
5 |
|
1 ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ....................................................................................................... |
5 |
|
1.1 Методы отделения корней.............................................................................................................. |
5 |
|
1.1.1 Постановка задачи......................................................................................................................... |
5 |
|
|
|
5 |
1.1.2 Табличный метод отделения корней............................................................................................ |
||
1.1.3 Графический метод отделения корней......................................................................................... |
6 |
|
1.1.4 Метод интервалов отделения корней......................................................................................... |
6 |
|
1.2 Методы уточнения приближенных корней................................................................................... |
7 |
|
1.2.1 Постановка задачи.......................................................................................................................... |
7 |
|
1.2.2 Оценка погрешности приближенного корня............................................................................... |
7 |
|
1.2.3 Метод половинного деления......................................................................................................... |
8 |
|
1.2.3.1 Алгоритм метода половинного деления.................................................................................................................. |
10 |
|
1.2.4 Метод итераций.......................................................................................................................... |
10 |
|
1.2.4.1 Алгоритм метода итераций....................................................................................................................................... |
14 |
|
1.2.5 Метод Ньютона............................................................................................................................ |
15 |
|
1.2.5.1 Алгоритм метода Ньютона........................................................................................................................................ |
16 |
|
1.2.6 Метод хорд.................................................................................................................................... |
17 |
|
1.2.6.1 Алгоритм метода хорд............................................................................................................................................... |
18 |
|
1.2.7 Комбинированный метод............................................................................................................ |
18 |
|
1.2.7.1 Алгоритм комбинированного метода...................................................................................................................... |
19 |
|
1.2.8 Пример решения уравнения........................................................................................................ |
19 |
|
1.2.8.1 Метод половинного деления ................................................................................................................................... |
20 |
|
1.2.8.2 Метод итераций ........................................................................................................................................................ |
22 |
|
1.2.8.3 Метод Ньютона ......................................................................................................................................................... |
23 |
|
1.2.8.4 Метод хорд.................................................................................................................................................................. |
24 |
|
1.2.8.5 Комбинированный метод.......................................................................................................................................... |
26 |
|
1.2.9 Уточнение корней уравнений в Excel с помощью циклической ссылки............................... |
27 |
|
1.2.9.1 Метод половинного деления .................................................................................................................................... |
28 |
|
1.2.9.2 Метод итераций.......................................................................................................................................................... |
29 |
|
1.2.9.3 Метод Ньютона.......................................................................................................................................................... |
29 |
|
1.2.9.4 Метод хорд.................................................................................................................................................................. |
30 |
|
1.2.9.5 Комбинированный метод.......................................................................................................................................... |
31 |
|
1.2.10 Решение уравнений средствами MathCAD.............................................................................. |
31 |
|
ПРИЛОЖЕНИЕ ................................................................................................................................... |
33 |
|
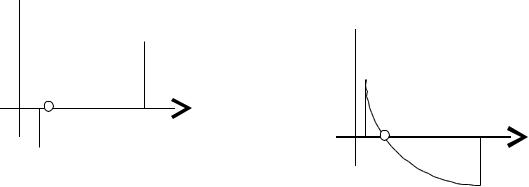
4
ВВЕДЕНИЕ
В данных методических указаниях рассматриваются численные методы решения уравнений на языке программирования Visual Basic For Application (VBA), с помощью циклической ссылки MS Excel и средствами MathCAD.
1 ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ
1.1Методы отделения корней
1.1.1Постановка задачи
Пусть
f(x)= 0 |
(1) |
– некоторое уравнение. Число ξ называется корнем или решением данного уравнения, если оно, будучи подставлено в уравнение, обращает его в равенство, т. е. f(ξ) = 0. Число ξ называют нулем функции y = f(x).
Выделение из области определения функции f(x) отрезков [ai; bi], в каждом
из которых содержится один и только один корень ξi уравнения f(x) = 0, называют
отделением корней уравнений.
Достаточные условия существования корней на заданном интервале (a; b) дает следующая теорема.
Теорема 1. Если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a; b], то внутри этого отрезка содержится по меньшей
мере один корень уравнения f(x) = 0, т. е. найдется хотя бы одно число ξ (a; b) такое, что f(ξ) = 0.
Корень ξ заведомо будет единственным, если производная f ′(x) существует и сохраняет постоянный знак внутри интервала (a; b) (см. рис. 1).
y
y
α
ξ |
β x |
β |
|
||
|
α ξ |
x |
|
f ′(x) > 0 |
f ′(x) < 0 |
|
Рис. 1 |
|
1.1.2 Табличный метод отделения корней
Табличный метод отделения корней состоит в том, что составляют таблицу значений функции y = f(x) в ряде промежуточных точек x = a1, a 2, ..., a k, ak+1, ..., an,