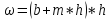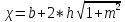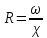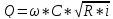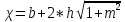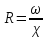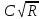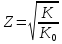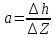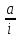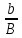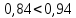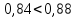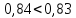КР гидравлика

Задание 1. Вариант 3

Определить равнодействующую силу избыточного давления воды на плоский затвор прямоугольного сечения, а также расстояние ℓ_ц.д. до центра давления на затвор слева и справа. Расчет силы и ц.д. произвести аналитическим и графоаналитическим способом.

h₁ = 1,3 м

h₂ = 0,7 м

b = 1,2 м

α = 75^о

Определяем силу избыточного давления на стенку АВ с левой стороны Р_{изб 1} :

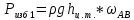
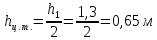
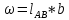
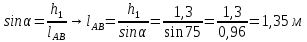
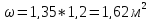
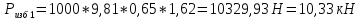
находим расстояние до ц.д. силы

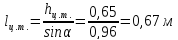
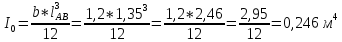
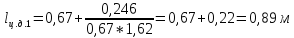
Определяем силу избыточного давления на стенку СВ с правой стороны Р_{изб 2}:

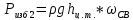
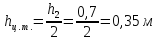
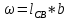
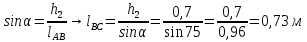
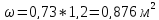
находим расстояние до ц.д. силы

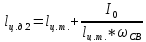
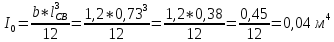
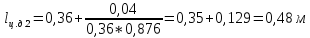
Строим эпюру избыточного давления:

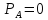
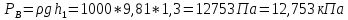
Задание 2. Вариант 3

Определить напор необходимый для пропуска заданного расхода воды через гидравлический трубопровод состоящий из двух последовательных соединённых участков труб с разными диаметрами.

Q = 12 ^л/_с = 0,012 ^м3/_с

Р₀ = 96 кПа = 96000 Па

d₁ = 125 мм = 0,125 м

d₂ = 100 мм = 0,1 м

ℓ₁ = 82 м

ℓ₂ = 66 м

t⁰ = 12⁰ С

∆ = 0,5 мм

Схема 1.

Уравнение Бернулли

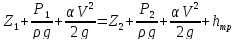
Составляем уравнение Бернулли для сечений 1-1 и 2-2 относительно горизонтальной плоскости 0-0

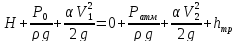
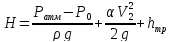
Находим среднюю скорость в трубах

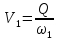
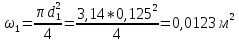
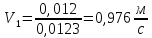
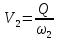
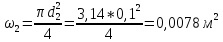
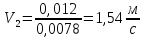
Определяем потери напора:

Определяем местные потери h_м:

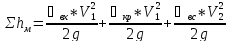
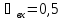
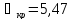при α_кр = 30⁰

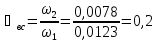
м

Определяем потери по длине :

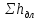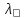- коэффициент гидравлического трения зависящий от режима движения жидкости

Находим число Рейнольдса в первой трубе:

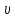– кинематический коэффициент вязкости, зависит от t⁰ воды

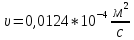при t⁰ = 12⁰

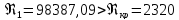
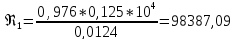
В первой трубе турбулентный режим движения.

Находим число Рейнольдса во второй трубе:

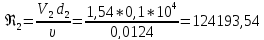
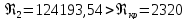
Во второй трубе турбулентный режим движения.

Для турбулентного режима движения коэффициент гидравлического трения определяется по формуле:

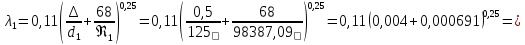
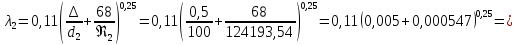
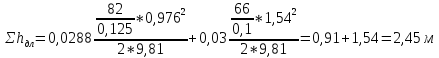
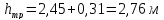
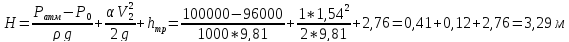
Задание 3. Вариант 3

Определить время полного опорожнения резервуаров.

Ω₁ = 2 м²

Ω₂ = 4,2 м²

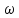= 16 см² = 0,0016 м²

h₁ = 2,4 м

h₂ = 3 м

Время полного опорожнения определяется по формуле:

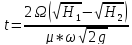
H₁ = h₁ + h₂ = 2,4 + 3 = 5,4 м

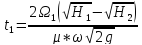
H₂ = h₂ = 3 м

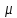= 0,62 – коэффициент расхода отверстия

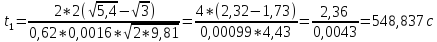
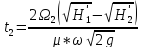
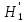= h₂ = 3 м

= 0

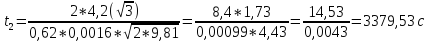
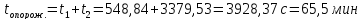
Задание 4. Вариант 3

Из напорного бака с постоянным уровнем вода подается потребителям по трубопроводу, состоящему из двух последовательно соединённых участков гидравлически длинных труб. Требуется: 1. определить расчетный расход на каждом участке; 2. вычислить потери напора на каждом участке, пользуясь таблицами для гидравлически длинных труб.

Q_В = 48 ^л/_с

Q_р1 = 0 ^л/_с

Q_р2 = 46 ^л/_с

d₁ = 300 мм

d₂ = 250 мм

ℓ₁ = 340 м

ℓ₂ = 660 м

Новые чугунные

Последовательно соединение труб поэтому напор равен сумме напоров в каждой трубе

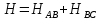
Участок АВ

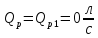
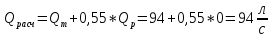
Находим скорость в трубе

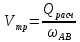
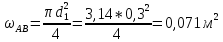
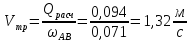
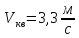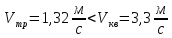По таблице 13.1 стр. 259 т.к. область не квадратичная. Ищем поправку стр. 592 табл. 4

стр. 593 табл. 5

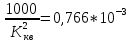
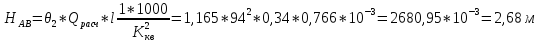
Участок ВС

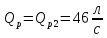
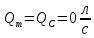
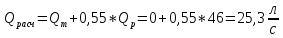
Находим скорость в трубе

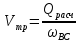
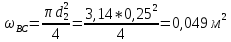
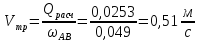
По таблице 13.1 стр. 259 т.к. область не квадратичная. Ищем поправку стр. 592 табл. 4

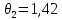
стр. 593 табл. 5

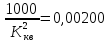
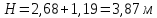
Задание 5. Вариант 3

Вода поступает по трубопроводу d и длинной ℓ при избыточном давлении Р₀. При резком закрытии задвижки установленной в конце трубопровода возникает гидравлический удар. Определить скорость распространения ударной волны и длительность фазы. Выяснить вид удара и определить максимально повышенное давление.

Q = 990 ^л/_с

d = 800 мм

е = 80 мм

ℓ = 0,9 км

Р₀ = 200 кПа

Т_з = 0 с

сталь

Находим скорость распространения волны гидравлического удара

для воды – сталь табл. 14.1 стр. 292

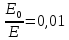
Находим фазу гидравлического удара

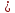
т.к. Т_з = 0 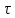= 1,32 то удар прямой

Определяем повышенное давление по формуле Жуковского

Находим среднюю скорость в трубе

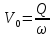
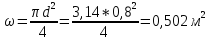
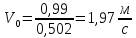
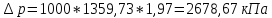
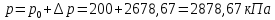
Задание 6. Вариант 3

Определить глубину, среднюю скорость и относительную ширину при равномерном движении в канале трапецеидального сечения.

Q = 10 ^м3/_с

b = 4 м

m = 1,5

i = 0,0003

n = 0,02

Задачу решаем методом подбора по уравнению Шизи задаваясь рядом значений глубины h, расчеты сводим в таблицу

h, м	м2				м2/с
0,5	2,37	5,80	0,4	42,94	1,11
1,0	5,5	7,61	0,72	47,47	3,83
1,5	9,37	9,41	0,99	49,92	8,06
2,0	14	11,21	1,25	51,71	14,02

Проверяем канал на размыв, находим среднюю скорость в канале

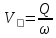
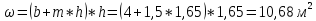
по табл. 16.3 стр. 330 при суглинке С_расч = 0,15*10⁵ Па и глубине 1,65 м определяем допустимую скорость на размыв V_доп = 1,25 ^м/_с

т.к. 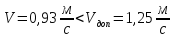то канал не размывается.

Задача 7. Вариант 3

В конце канала, рассчитанного в задаче 6, устроено сооружение, которое нарушает равномерное движение. При этом устанавливается конечная глубина и формируется кривая подпора или спада.

Определить:

1. Критическую глубину h_кр в начале канала при расходе Q;

2. Сравнивая h₀, h_кр, h_кон выяснить зону формирования кривой свободной поверхности (привести расчетную схему), с помощью дифференциального уравнения неравномерного движения определить вид кривой и назначить начальную глубину.

Q = 10 ^м3/_с

b = 4 м

m = 1,5

i = 0,0003

h₀ = 1,65 м

h_кон = k * h₀ = 1,5*1,65 = 2,47 м

Определение критической глубины с трапецеидальном сечении

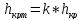
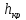– критическая глубина в прямоугольном русле

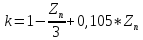
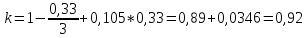
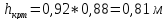
Проводим анализ кривой свободной поверхности по уравнению неравномерного движения

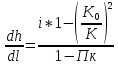
Составляем расчетную схему

Для оценки знака числителя сравниваем глубины – конечную и нормальную

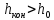, поэтому расход характеризуется при неравномерном движении 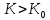, поэтому

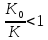
Для оценки знака знаменателя сравнивают глубины – конечную и критическую 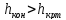, состояние потока спокойное

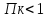
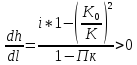
Глубины вдоль канала увеличиваются образую кривую подпора

Назначаем расчетные глубины

h_нач = 1,02*h₀ = 1,68 м

h_кон = 2,47 м

Расчет кривой подпора методом Чертоусова при х = 4,

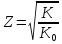
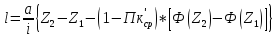
h, м	∆ h, м	ω, м2	В					Пк	1-Пк	1-Пкср		∆Z	Ф(Z)	∆ Ф(Z)			ℓ, м
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
1,68	0,79	10,95	9,04	10,05	1,08	52,56	575,53	0,069	0,931	0,928	0,98	0,46	1,52	- 0,62	1,71	5700	5871
2,47		19,03	11,41	12,9	1,47	64,15	1220,77	0,075	0,925		1,44		0,9

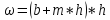
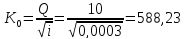
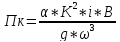
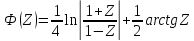
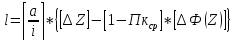
при h_нач = 1,68 м

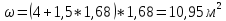
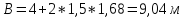
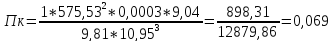
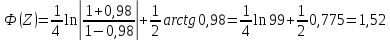
при h_кон = 2,47 м

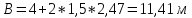
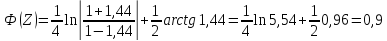
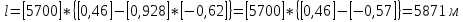
Задача 8. Вариант 3

При входе в трапецеидальный канал проектируется регулятор, работающий как прямоугольный водослив с широким порогом. Высота водослива со стороны верхнего и нижнего бьефов равны 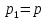. При пропуске расчетного расхода Q глубина воды в канале перед водосливом равна h_к, за водосливом h_б. Определить ширину регулятора.

Q = 30 ^м3/_с

h_б = 2,65 м

∆Z = 0,4 м

b_к = 6 м

m = 2

р₁ = 0,2 м

Регулятор – это водослив с широким порогом размерами

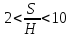
Определяем напор над водосливом

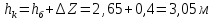
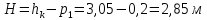
Находим скорость подхода к водосливу

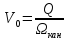
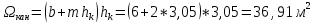
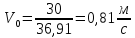
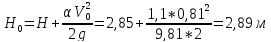
т.к. коэффициент потопления (ϭ_п) коэффициент расхода (m) зависят от ширины регулятора (b) которое нам не известно, то выделяем из формулы расхода водослива комплекс неизвестных величин

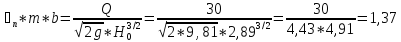
Расчет сводим в таблицу

b, м		m	К2	подтопление		ϭп	ϭп*m*b
3	0,25	0,31	0,94	подтоплен	0,20	0,97	0,94
4	0,33	0,32	0,88	подтоплен	0,26	0,98	1,25
5	0,41	0,33	0,83	не подтоплен		1	1,65

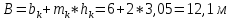
т.к. поток при входе из канала на регулятор сжимается и порог на входе р₁ ≠ 0, а сопряжение в плане по типу обратно стенки, то коэффициент расхода m определяется по формуле Смыслова

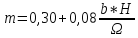
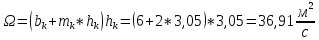
К₂ определяем по таблице 22.3 стр. 439

Проверяем подтопление водослива

Водослив подтоплен если 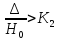, тогда ϭ_п находим по таблице 22.4 стр. 441

Водослив не подтоплен если 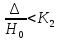, тогда ϭ_п = 1

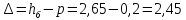
b = 4,3 м По ГОСТу принимаем ширину регулятора b = 4,5 м

Задача 9. Вариант 3

Водосливная плотина – это водослив практического профиля с криволинейным очертанием имеет n одинаковое число пролетов с затворами на гребне водослива, поддерживающими НПУ (нормальный подпорный уровень). Ширина одного пролета b. За профилирующий напор принимается напор при НПУ. Скорость подхода к водосливу V₀. Высота водослива со стороны ВБ и НБ равны p₁ = p.