50

Часть 2.Элементы теории определённого и кратного интеграла.

Введение.

Прежде чем доказывать условия существования кратного интеграла, необходимо рассмотреть простые достаточные условия существования определённого интеграла , а именно: непрерывность подинтегральной функции и компактность области интегрирования – отрезка (точнее, сегмента)как множества точекчисловой оси, удовлетворяющих двойному неравенству:. К сожалению, тот факт, что определённый интеграл от функции, не меняющей знак в области интегрирования, есть именноориентированнаяплощадь криволинейной трапеции, в учебной литературе недостаточно подчёркивается. Наша основная цель – более внимательно рассмотреть такие фундаментальные понятия, как площадь и объём.

§ 1.Определённый интеграл.

Обозначение.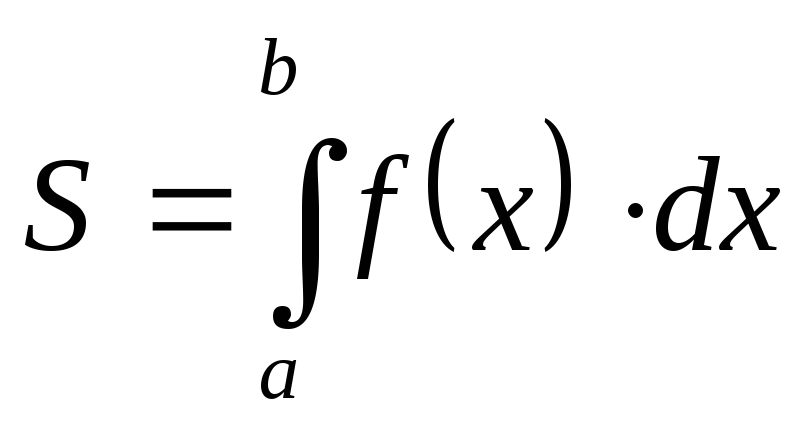. Здесьесть подинтегральная функция,и- пределы интегрирования, причём- нижний предел,- верхний предел,-переменная интегрирования – так называемаясвязаннаяпеременная. Для этой переменной можно менять обозначение. Например, справедливо равенство:. Если похожая переменная встретится в верхнем или нижнем пределе интеграла, то это –свободнаяпеременная, которую нельзя переобозначать (во всяком случае, без дополнительных переобозначений в других местах).

Определение 1.Определённый интеграл(геометрический) для знакопостоянной подинтегральной функции есть ориентированная площадь криволинейной трапеции, то есть фигуры, определяемой множеством точек, координаты которых удовлетворяют неравенствам:илииили.

Ориентированная площадьесть площадь со знаком. Знак этой площади определяется следующим образом (см. рисунок).

1 случай.и. В этом случае.

2 случай.и. В этом случае.

3 случай.и. В этом случае.

4 случай.и. В этом случае.

Определение 1.Определённый интеграл(геометрический) для знакопеременной подинтегральной функции есть алгебраическая сумма определённых интегралов от её знакопостоянных частей.

Пример..

Теорема существования определённого интеграла.

Если подинтегральная функция непрерывна на сегменте(иначе, для любого, такого, чтоилипредел от функции будет равен функции от предела, то есть:) , тосуществует.

В следующей лекции после уточнения понятия интеграла требование на поведение подинтегральной функции внутри области интегрирования будет несколько ослаблено.

§ 2. Способы вычисления «наивного» определённого интеграла.

Вычисление определённого интеграла как площади криволинейной трапеции может быть выполнено двумя способами.

Первый способ– вычисление площади путём замены криволинейной трапеции на близкую по площади фигуру с последующим прямым суммированием частей этой фигуры.

Второй способ- составление дифференциального уравнения для площади криволинейной трапеции с последующим его решением.

Примервычисления по первому способу. Вычислим.

Делим отрезок наравных частей. Заменяем криволинейную трапецию (точнее, криволинейный треугольник),на близкую по площади ступенчатую фигуру (см. левый рисунок).

Обозначим: . Тогда площадь ступенчатой фигуры (интегральная сумма), приблизительно равная интегралу (при больших) будет равна (с точки зрения алгебраиста):

.

Левую часть приблизительного равенства преобразуем так:

.

Раскрывая скобки в числителе и вспоминая тригонометрическое равенство:, преобразуем предыдущее равенство следующим образом:.

Учитывая, что внутренние слагаемые взаимно уничтожаются при приведении подобных членов, получаем:

. Переходя к пределу прии учитывая, чтои что дробьстремится к единице как первый замечательный предел, получаем в пределе:.

Геометр решил бы эту задачу ещё проще (см. правый рисунок выше). На рисунке ,,.

Примервычисления по второму способу. Вычислим.

Пусть . Тогда. Здесь- бесконечно – малое колебание непрерывное функциина отрезке длинойот точкидо точки. Общее решение этого дифференциального уравненияесть- неопределённый интеграл как множество первообразных. Константаищется исходя из того, что(площадь отрезка от точкидо точкиравна нулю). Итак:иили- решение задачи скорее по Ньютону, чем по Лейбницу.