§ 10Теорема Пуанкаре и её использование при вычислении поверхностных интегралов второго рода.

Этот замечательный результат А. Пуанкаре будем использовать, прежде всего, как мнемоническое правило для формулировок целого ряда теорем, поэтому формулируем теорему Пуанкаре в её наиболее абстрактном виде.

Итак, теорема Лейбница – Ньютона – Грина – Стокса – Остроградского – Гаусса-Пуанкаре имеет вид: .

Комментарии(пояснения) к теореме.

1. Объём есть- мерная ограниченная область в пространстве той же размерности. Ограниченность следует понимать как ограниченность расстояния между любыми двумя точками, расположенными внутри области, то есть эти расстояния не могут превышать некоторого заданного числа.

2. Далее, есть топологическая граница этой области – поверхность размерности. Граница понимается с том смысле, что любой-мерный шар с центром в точке границы содержит внутри себя как точки, принадлежащие области, так и точки, не принадлежащие к ней. В то же время для внутренних и внешних точек области существуют шары, содержащие только внутренние или только внешние точки области.

3. В левой части равенства имеем - кратный интеграл. Кружок на символе двойного интеграла означает, что у самой границы отсутствует граница. Иначе говоря,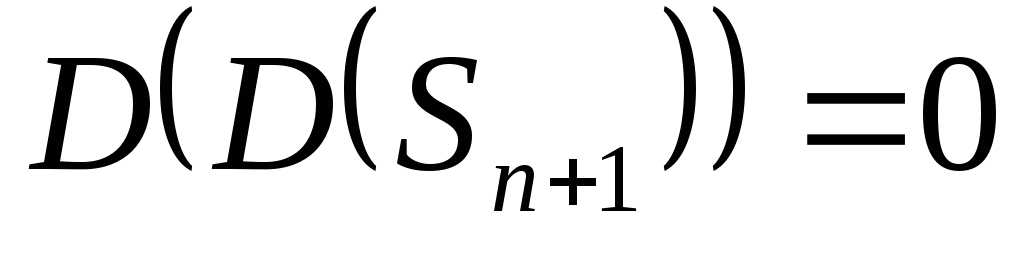известный топологический факт.

4. Дифференциальный оператор имеет вид:, причём объёмпогружен в пространстворазмерности.

5. Внешнее произведение обладает свойствами произведения Грассмана, а именно: линейностью и антикоммутативностью.

Более подробно смысл теоремы будет ясен из дальнейшего изложения материала. Рассмотрим теперь частные случаи теоремы Пуанкаре.

1.Теорема (формула) Грина.

Здесь ,,,,.

Имеем:

.

Итак: - формула Грина.

2.Теорема (формула) Стокса.

Здесь ,,,,

.

Имеем:

.

Итак:

- формула Стокса.

В векторных обозначениях формула принимает вид:

или: .

3.Теорема (формула) Гаусса – Остроградского.

Здесь ,,,,

.

Имеем:

.

Проделывая выкладки, аналогичные предыдущим, получаем формулу Гаусса – Остроградского:

.

В векторных обозначениях эта теорема принимает вид:

, где:,,

.

4. О доказательстве теоремы Пуанкаре.

Нижеследующие рассуждения показывают метод доказательства этой теоремы в частном случае одного слагаемого дифференциальной формы второго порядка. Рассмотрим выражение , где. Тогда подинтегральное выражение может быть представлено в виде:

Очевидно, в данном случае мы имеем разложение определителя по верхней строке. Примем без доказательства тот факт, что подходящей параметризацией объёмаего поверхностьможет быть разбита на 6 граней, причём на противоположных гранях один параметр из трёх сохраняет постоянное значение.Пример: раздувание куба в пространстведо сферы в пространстве.

Пояснение. Дифференциалследует понимать как дифференциал (главную линейную часть приращения) вдоль возрастания параметра:

.

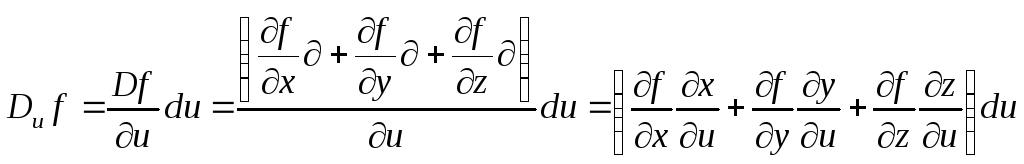Аналогично расписываются и.

Выполняя интегрирование в первом слагаемом суммы трёх интегралов :

по параметру, во втором – по, а в третьем – по, получаем следующее выражение:

.

В первом слагаемом последнего выражения интегрирование производится по противоположным граням кривоповерхностного куба в пространстве , соответствующим граням куба (точнее, параллелепипеда):ив пространстве. Аналогичные рассуждения справедливы и для противоположных гранейи.

Иногда рассуждения проводятся следующим образом. Строим криволинейную сетку разбиения области интегрирования , соответствующую прямоугольной сетке. Затем тройные интегралы (например,) по бесконечно тонким слоям, где один из параметров (u,vилиw) отличается на бесконечно – малую величину, представляем в виде приближённых разностей интегралов по близким поверхностям. Тогда интегралы по внутренним поверхностям криволинейной сетки взаимно уничтожаются и остаются только разности интегралов по криволинейным граням куба в пространстве, соответствующим граням куба.

Далее, поскольку ориентации по противоположнымграням кубапротивоположны(если смотреть на них извне куба), то для сохраненияединойориентации по всем граням куба, необходимо изменить ориентации и знаки перед функциями на гранях. Тогда сумма шести слагаемых выражения:превратится в интеграл по всемшестиграням куба в пространстве, то есть в.

Читателю рекомендуется провести аналогичные рассуждения для теорем Грина и Стокса.

5.Теорема Лейбница – Ньютона.

Здесь ,,,.

- форма «нулевого» порядка. Здесь.

Теорема формально выглядит так: или так:.

Удобно также представить теорему как «перепрыгивание» дифференциала с цепи на коцепь, в данном случае:(пользуемся топологической терминологией):

.

6.Пример использования теоремы Пуанкаре.

Вычислим контурный интеграл , гдеи- круг, и, соответственно, окружность радиуса.

Решение. По теореме Пуанкаре:

.

Проверка. Вычислим контурный интеграл непосредственно параметризацией окружности:.

Имеем:

=.