7.7. Методы получения колебаний с однополосной модуляцией

В § 7.1 упоминался один метод формирования сигналов с ОМ, кото­рый заключается в использовании для этой цели амплитудного модуля­тора и полосового фильтра. В дальнейшем метод стали называть фильтровым. Долгое время этот метод казался несовершенным, по­скольку требовал для своего осуществления высококачественных, а зна­чит дорогих и сложных полосовых фильтров. Поэтому в разное время было предложено много других методов, которые реализуются без таких фильтров. Среди них наибольшую известность получили фазоразностный метод, фазофильтровой метод Уивера, синтетический метод Верзунова.

Тщательный анализ фазоразностного и фазофильтрового методов показал, что поскольку эти методы основаны на компенсации нежела­тельных продуктов модуляции (несущей, второй боковой), невозможно получить высокие и устойчивые по времени показатели модуляторов, построенных по этим методам. Что касается синтетического метода Верзунова то по сути дела — это метод переноса каким-то образом уже сформированного однополосного сигнала на другую несущую частоту.

В 40 — 50-х годах были достигнуты крупные успехи в разработке высококачественных полосовых ВЧ фильтров, использующих в качест­ве резонаторов кварцевые и стальные резонаторы. По этим причинам фильтровой метод формирования сигналов с ОМ стал преобладающим и в настоящее время широко используется в многоканальных устройст­вах. В последнее время разработаны и стали внедряться однополосные модуляторы, использующие цифровую обработку аналоговых сигна­лов. Поэтому ниже рассматриваются принципы осуществления и осо­бенности реализации только для фильтрового и одного варианта цифрового метода получения колебаний с ОМ.

Принципиальная основа фильтрового метода заключается в том, что предварительно получается колебание с AM, а затем с помощью поло­сового фильтра выделяется колебание в желательной боковой полосе и подавляются колебания несущей и в другой боковой. На рис. 7.10 при­ведены структурная схема однополосного модулятора, состоящая из балансного модулятора и полосового фильтра, и диаграммы спектров сигналов в различных точках этой схемы. Если на входы балансного модулятора подать модулирующее колебание U_Ω с частотой Ω = 2πF и колебание U_ω с несущей частотой ω₀ = 2πf₀, то спектр колебания на выходе модулятора будет состоять из двух боковых полос и сильно подавленной несущей (рис. 7.10,в).

Полоса пропускания полосового фильтра выбирается так, чтобы пропускались составляющие только верхней (f₀ + F₁...f₀ + F₂) или только нижней (f₀ − F₁...f₀ − F₂) боковых полос. Спектры колебаний на выходе модулятора для этих случаев показаны на рис.7.10, г, д.

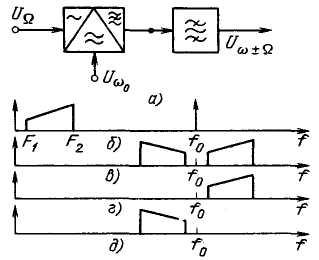
Рис. 7.10. Структурная схема однопо­лосного

фильтрового модулятора и эпюры сигналов

Основные качественные показатели модуляторов, построенных с применением фильтрового метода, обусловлены входящими в них эле­ментами: нелинейность амплитудной характеристики — балансными модуляторами и их числом, подавление нежелательных сигналов — полосовыми фильтрами.

Рассмотрим вопрос о нелинейности АХ. В модуляторах, собранных по схемам рис.7.11, используются трансформаторы НЧ (Тр₁), трансфор­маторы ВЧ (Тр₂) и диоды с возможно малым напряжением отсечки тока. Иногда для построения модуляторов используют биполярные или поле­вые транзисторы, варикапы и стабилитроны с дополнительным смеще­нием.

Анализ работы простейшего модулятора можно выполнить, вос­пользовавшись эквивалентной схемой (рис. 7.12,а), если предваритель­но пересчитать параметры источника НЧ напряжения U_Ω и R_г, а также нагрузки R_н в контур, где включены диод и источник ВЧ напряжения и течет ток i'_н. При этом следует учесть, что к диоду приложено напряжение и'_Ω + и_ω0 = n₁U_ΩcosΩt + U₀cosωt и что этот диод можно заменить клю­чом с сопротивлением R_п, кото­рый открыт при и'_Ω + и_ω0 > е_д0 [4].

Спектр тока i'_н в области частот 0 < f < 1,5f₀ показан на рис. 7.11, а. Он содержит постоянную компоненту (которая отсутствует в нагрузке R_H реального модулятора из-за наличия трансформатора Тр₂), компоненты с частотами исходных коле­баний F и f₀, компоненты модуляции I(f₀ ± F) c частотами f₀ + F и f₀ − F, гармоники частоты f₀, а также компоненты, не показанные на рис. 7.11, а, с комбинационными частотами вида mf₀ ± nF, где m = 1, 2, ... и n = 1, 2, ...

Ток i'_н имеет форму усеченных косинусоидальных импульсов (рис. 7.12,б). Угол отсечки этого тока θ = arccos (n₁U_ΩcosΩt/U₀) зависит, строго говоря, от обоих напряжений: U_Ω и U₀. Чтобы обеспечить линей­ность модуляционной характеристики I(f₀ ± F) = f(U_Ω) этого модулятора, необходимо сделать цепь тока i'_н квазилинейной, т. е. добиться незави­симости работы ключа K от величины модулирующего напряжения U_Ω. Этого можно достичь, если угол отсечки θ не будет зависеть от U_Ω, т. е. если выполняется условие U₀>>n₁U_Ω [14].

Рис. 7.11. Балансные модуляторы и эпюры

спектров выходного сигнала

Рис. 7.12. Эквивалентная схема диода в БМ и эпюра токов

Анализ работы более сложных модуляторов проводится как бы в два этапа: сначала так же, как и для простейшего, определяют токи через диоды, а затем находят результирующий ток в нагрузке.

В модуляторе рис. 7.11,б вследствие симметричности схемы относи­тельно источника колебаний несущей частоты в спектре выходного сигнала компонента с несущей частотой обычно сильно подавлена. Эта схема достаточно практична, так как возможная точность симметрии, от которой зависит степень подавления компоненты с несущей частотой f₀, определяется лишь точностью подбора диодов в мостике. Примене­ние диодных сборок или согласованных пар биполярных или полевых транзисторов обеспечивает подавление несущей на 35...45 дБ. Широкое распространение получили балансные модуляторы, собранные по схеме рис. 7.11,в. Основным их достоинством наряду с меньшим числом неже­лательных спектральных компонент тока i'_н является на 2...3 дБ меньшее затухание b=20lg(U_Ω/U(f₀ ± F)), чем в модуляторе по схеме рис. 7.11, б. Объясняется это тем, что балансный модулятор состоит как бы из двух симметричных модуляторов, работающих в двухтактном режиме.

Для подавления несущей и нежелательной боковой в однополосном модуляторе (см. рис. 7.10,а) служит полосовой фильтр. Этот фильтр должен иметь малую неравномерность затухания в полосе прозрачнос­ти и очень крутые скаты, поскольку частотный интервал между ближай­шими краями боковых, равный 2F_H, где F_H — нижняя модулирующая частота, очень мал по сравнению с несущей частотой. Из теории фильт­ров известно, что для реализации таких фильтров требуется высокая добротность контуров, из которых образуется фильтр. Для получения необходимого подавления несущей и нежелательной боковой полосы используются часто трех-четырехзвенные фильтры из звеньев типа т.

Оценим необходимую добротность резонаторов для фильтра на при­мере П-образного звена, показанного на рис. 7.13. Пусть частота f_∞1 соответствует частоте f₀, а частоты f_ср1 и f_ср2 — границам полосы канала B₁. Из теории фильтров известно, что для получения малой неравномер­ности затухания в полосе пропускания и большого затухания в полосе задержания необходимо, чтобы контуры, настроенные на частоты f₀ и f_ω (L₂C₂ и L₃C₃), имели в полосе пропускания чисто реактивное сопротивление. Это означает, что половина полосы пропускания этих контуров Δf должна быть меньше интервалов f_ω...f_ср2 или f_ср1...f₀, т. е. Δf = (f_ср1 − f₀). Здесь l — коэффициент запаса, зависящий от необходимого затухания в полосе задержания фильтра и от величины m(l ≥ 3...5). Если теперь учесть, что для лучшей равномерности затухания в полосе пропускания принимают т = 0,4...0,6, при которых параметр полосы φ(m) = (f_ср1 − f₀)/( f_ср − f_ср1) ≈ 0,15 и что добротность контуров Q = f /2Δf, то после простых преобразований можно получить приблизительную формулу Q = lf₀/φ(m)ΔF.

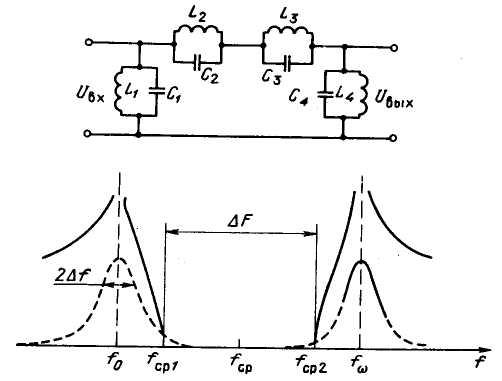
Рис. 7.13. Звено полосового фильтра и его АЧХ

Расчет по этой формуле для φ(m) = 0,15, Δf = 3100 Гц и l = 5 показы­вает, что необходимые добротности контуров фильтра для частот f₀, равных, например, 20, 100 и 500 кГц, соответственно приблизительно равны 200, 1000 и 5000. Резонансные контуры, выполненные на катуш­ках с ферритовыми сердечниками, имеют добротность не выше 200...300. Поэтому при использовании фильтров с такими контурами первую несущую частоту f₀ можно брать не выше 25 кГц.

В современных модуляторах применяются фильтры с кварцевыми или стальными резонаторами. При добротности кварцевых резонато­ров около 10...20 тыс. и выше можно создавать двух-трехзвенные высо­кокачественные фильтры для частот 5... 10 МГц и даже выше. Однако до сих пор широко распространены кварцевые фильтры для частот 100...150 кГц, так как именно для этих частот возможно изготовление дешевых резонаторов с малым ТКЧ.

В последние годы были разработаны так называемые интегральные кварцевые фильтры, выполненные на одном кристалле, благодаря чему удалось, пока в опытном порядке, резко снизить температурные нестабильности и создать высококачественные фильтры для частот до 10...15 МГц.

В передатчиках низовой телефонной связи с допустимой неравно­мерностью АЧХ 3...6 дБ широко применяют электромеханические фильтры, резонаторы которых выполнены в виде дисков из специальной легированной стали, имеют добротность до 5000 и сравнительно низкий ТКЧ. Канальные фильтры, содержащие от 7 до 13 таких резона­торов, выполняют для частот до 500 кГц.

Таким образом, первая поднесущая частота f₀ может выбираться в пределах 100...500 кГц и для транспонирования передаваемого сигнала в рабочий диапазон частот необходимо использовать еще одно — три преобразования. Этой цели служит тракт переноса ТП (рис. 7.14), со­стоящий из нескольких балансных модуляторов (БМ), усилителей для поддержания необходимых уровней сигналов на входах БМ (на схеме усилители не показаны) и фильтров.

Для того чтобы выходной сигнал с частотой f_н оказался в рабочем диапазоне частот передатчика и при этом не требовались в ТП перестра­иваемые фильтры, реализуется обычно следующий метод. Сформиро­ванный в однополосном модуляторе ОМ сигнал с несущей частотой f₁ с помощью последующих одного-двух преобразований переносится на частоту значительно более высокую, чем верхняя частота рабочего диа­пазона. Затем с помощью последнего преобразователя сигнал е ОМ переносится непосредственно в рабочий диапазон. На рис. 7.14 для иллюстрации и поэтому без соблюдения масштаба показаны ориенти­ровочные значения частот в разных точках ТП применительно к возбу­дителю для KB передатчика с рабочим диапазоном частот 1...30 МГц.

При таком решении ТП нет необходимости в перестраиваемых фильтрах, поскольку к входам БМ₃ подводятся ОМ сигнал с несущей 80 МГц и сигнал от синтезатора с дискретными частотами в диапазоне 81...110 МГц (сетка частот). Неперестраиваемый фильтр нижних частот выделяет сигналы с разностной частотой f_н — 80 МГц, т. е. на любой частоте диапазона 1...30 МГц. Входные частоты БМ₃ и их гармоники фильтр подавляет, поскольку частота среза для него выбирается немно­го выше 30 МГц.

Рис. 7.14. Частотный план и структурная схема тракта переноса

Число преобразователей в ТП зависит от ряда факторов: частоты f₁, на которой формируется ОМ сигнал, целесообразных параметров фильтров и требуемого рабочего диапазона частот. Реализация фильт­ров в ТП заметно легче, чем в ОМ, поскольку для них относительная расстройка между пропускаемой и подавляемой полосами заметно больше, чем для фильтра в ОМ (см. рис. 7.10,а).

В ТП, как и в ОМ, необходима высокая линейность сквозной АХ, зависящая от типов и режимов ЭП, применяемых в БМ.

Выше было уже отмечено, что операция однополосной модуляции по существу является операцией переноса спектра исходного модулиру­ющего сигнала (то же однополосного, но с нулевой несущей частотой) на другой частотный уровень. Для выполнения этой операции могут использоваться как аналоговые устройства (описанный выше ОМ с БМ и полосовым фильтром), так и устройства цифровой обработки сигна­лов. Применение цифровых устройств, в частности однополосных мо­дуляторов, базируется на хорошо развитой теории и богатой элементной базе [7, 22, 36 и др.].

В устройствах цифровой обработки сигналов аналоговый сигнал предварительно переводится в цифровую форму (цифровой сигнал) с помощью АЦП, подвергается обработке и затем с помощью ЦАП ре­зультирующему сигналу возвращается аналоговая форма. Существует несколько алгоритмов для операции переноса спектра цифрового сиг­нала. На рис. 7.15 показана схема одного такого алгоритма. Здесь ис­ходный цифровой сигнал умножается на комплексный сигнал с частотой γ ≈ (F_н + F_в)/2, при этом происходит сдвиг спектра и образуется комплексный цифровой сигнал. Затем повышается частота дискретиза­ции (интерполяция) и производится фильтрация ненужных составляю­щих. Далее осуществляется перенос спектра компонент комплексного сигнала и выделяется вещественная часть цифрового сигнала Y, т. е. цифровой сигнал, соответствующий однополосному с несущей часто­той β.

Устройство, реализующее схему рис. 7.15, содержит два цифровых ФНЧ, имеющих довольно сложный алгоритм, если необходимо полу­чить приемлемые показатели этих фильтров.

Рис. 7.15. Структурная схема цифрового однополосного модулятора

Другой алгоритм получения однополосного модулированного сиг­нала (т. е. переноса спектра исходного модулирующего сигнала

к частоте ω₀) состоит из последовательности следующих операций.

1. Добавление к u_м(t) постоянной величины H, соответствующей желаемой амплитуде колебания с несущей частотой ω₀.

2. Получение сигнала , сопряженного с исходным с помощью пре­образования Гильберта и имеющего тот же спектр, что и у исходного сигнала.

3. Получение модулирующего сигнала в комплексной форме (анали­тический сигнал): w = Н + и_м + j·u_м.

4. Умножение сигнала w на комплексный сигнал с частотой ω₀: s = wv.

1. Выделение вещественной части этого произведения в виде

.

Сигнал s_OM имеет такой же спектр, что и у исходного и сопряжен­ного ему сигналов и_м и , но он оказался перенесенным к частоте ω₀. Другими словами, получен однополосный сигнал, у которого Н и ω₀ — амплитуда и частота несущего колебания.

Алгоритм имеет еще одно полезное свойство: наличие исходного u_м и сопряженного с ним сигналов позволяет найти огибающую исход­ного сигнала с добавлением постоянной величиныН:

.

Наконец, получив однополосный сигнал s_OM и разделив его на A(t), имеем сигнал с единичной амплитудой и угловой модуляцией cos[ω₀t + Ψ(t)].

Операции нахождения огибающей и сигнала с угловой модуляцией соответствуют операциям линейного детектирования и бесконечного амплитудного ограничения. Выполнив перечисленные операции (при достаточно высокой разрядности n = 12...16 и корректных програм­мах), можно получить выходные сигналы с s_0M, A(t) и cos[ω₀t + Ψ(t)] с меньшими искажениями, чем в аналоговых устройствах, поскольку при цифровой обработке исключаются влияние нелинейности элементов БМ, нелинейность и постоянная времени амплитудного детектора и АФК, как правило, сопровождающая процесс амплитудного ограниче­ния в аналоговых устройствах.

На рис. 7.16 приведена структурная схема цифрового ОМ, в котором возможно получение однополосного сигнала в виде (7.6) и его составля­ющих, если возбудитель используется в передатчике с раздельным уси­лением. Реализуется также возможность регулировать амплитуду колебания несущей частоты.

Исходный сигнал поступает через согласующий усилитель к АЦП, превращается в цифровой сигнал и подводится к трансформатору Гиль­берта [5, 7, 6, 22]. К одному из выходных сигналов трансформатора Гильберта — ТГ (в приведенном случае — к сигналу косинусоидальных составляющих) в сумматоре добавляется сигнал Н в виде константы. Полученные таким образом сигналы на выходе сумматора (H + u_м) и на втором выходе подаются непосредственно и через инверторы к коммутатору (Ком). Движок коммутатора, фигурально говоря, приво­дится в действие сигналом тактовой частоты, может вращаться в том или обратном направлении и за четыре периода тактовой частоты дела­ет один оборот. По существу инверторы и ключ К выполняют операции 4 и 5 алгоритма, т. е. производят комплексное перемножение w и v и выделяют вещественную составляющую.

Таким образом, от движка коммутатора к элементу S/A поступает цифровой сигнал, соответствующий сигналу с ОМ, амплитудой несу­щей Н и частотой несущей f_н = f_т/4. При замкнутом ключе К сигнал с ОМ поступает к ЦАП₁ и превращается в аналоговую форму. В полосо­вом фильтре, подключенном к выходу ЦАП₁, снижается уровень внеполосных колебаний.

Рис. 7.16. Структурная схема цифрового однополосного

модулятора с трансформатором Гильберта

Квадраторы (X²), сумматор и извлекатель квадратного корня реали­зуют алгоритм получения огибающей. Сигналы огибающей подводятся к ЦАП₂, превращаются в аналоговую форму и через согласующий усилитель могут подаваться к тракту огибающей передатчика с раздельным усилением.

Сигналы огибающей в цифровом виде с выхода извлекателя подают­ся к делителю, в котором производится деление цифрового сигнала S_OM на цифровой сигнал A(t). Деление производится при разомкнутом ключе К. В этом случае к ЦАП₁ подводится цифровой сигнал, соответствующий сигналу с единичной амплитудой и угловой модуля­цией cos[ω₀t+Ψ(t)], несущая частота которого f_н = f_т/4. Ширина полосы пропускания фильтра выбирается так же, как и ширина полосы тракта огибающей передатчика.

При изготовлении такого рода модуляторов используются процессо­ры, регистры сдвига, мультиплексоры и другие элементы. При описании возбудителя для передатчика с раздельным усилением (см. § 7.5) было отмечено, что в тракте ВЧ сигнала необходимо устанавливать линию задержки. В рассматриваемом модуляторе возможны два решения: можно установить необходимую ЛЗ для аналоговых сигналов на выходе фильтра, где несущая частота постоянна; возможна также установка ЛЗ в виде сдвигающего регистра на выходе делителя S/A.

Что касается выбора тактовой частоты, то желательно, чтобы она была возможно выше: при этом будет выше f_н и увеличивается эффек­тивность подавления шумов квантования фильтром. Верхний же предел f_т определяется частотными характеристиками процессора. Например, в реализованном примерно 10 лет назад фирмой Brown Boveri возбуди­теле с цифровым модулятором тактовая частота равна 100 кГц и, следо­вательно, f_н = 25 кГц.

Современная элементная база позволяет построить аналогичное уст­ройство на аналоговых элементах. Трансформатор Гильберта в этом случае можно выполнить в виде двух линейных цепей с общим входом и двумя выходами [46]. В полосе модулирующего сигнала эти цепи должны иметь равномерную АЧХ и такие ФЧХ, чтобы разность фаз выходных сигналов на любой частоте была равной 90°. Однако решение с использованием цифровой техники оказывается существенно легче, практичнее и дает лучшие результаты (лучшее качество получаемых сигналов, независимость во времени характеристик, высокая воспроиз­водимость).