5. Основные логические и запоминающие элементы компьютера

Управляющие и преобразующие информацию цепи вычислительных машин состоят из совокупности логических элементов. Каждый элемент машины может иметь несколько входов и выходов. Сигналы на выходах логических элементов являются функциями входных сигналов. Основные логические операции реализуются в ЭВМ с помощью известных логических элементов ИЛИ, И, НЕ.

Логический элемент ИЛИ выполняет операцию логического сложения. Он имеет n входов и один выход. Сигнал на выходе этого элемента возникает при подаче сигнала хотя бы на один из его входов. Обозначение элемента ИЛИ на схемах показано на рисунке.

Логический элемент И выполняет операцию логического умножения. Он имеет n входов и один выход. Сигнал на выходе этого элемента имеет место только при подаче сигналов на все его входы.

Обозначение элемента И на схемах показано на рисунке.

Логический элемент НЕ выполняет логическую операцию отрицания. Он имеет один вход и один выход. Сигнал на выходе этого элемента возникает при отсутствии сигнала на его входе, то есть элемент НЕ инвертирует входной сигнал. Обозначение элемента НЕ на схемах показано на рисунке.

Наряду с логические элементами И, ИЛИ и НЕ в электронной машине также используются элементы типа И-НЕ, ИЛИ-НЕ, отличающиеся от предыдущих инвертированием выходного сигнала.

Логическая функция может быть представлена комбинацией логических операций сложения, умножения и отрицания, т.е. набор логических элементов трех типов (ИЛИ, И, НЕ) является функционально полным.

Логический элемент ИЛИ-НЕ, реализующий логическую операцию отрицания логического сложения, называют стрелкой Пирса (иногда ее обозначают). Таблица истинности операции ИЛИ-НЕ для двух аргументов представлена в таблице, а его условное обозначение — на рисунке.

X1	X2	X1 X2
0	0	1
0	1	0
1	0	0
1	1	0

При проектировании одних устройств может оказаться более удобным элемент ИЛИ-НЕ, а при проектировании других элемент И-НЕ.

Принцип построения сложных логических устройств. Рассмотрим построение только комбинационных логических схем.

Перед проектированием логической схемы в цифровых устройствах бывает задана таблица переключений — таблица истинности устройства, в которой даны входные сигналы и соответствующие каждому сочетанию входных сигналов выходные сигналы. Первый этап проектирования состоит в отыскании такой логической функции, которая соответствует таблице истинности устройств.

Функциональную схему, реализующую сложную логическую операцию, можно построить из основных логических элементов с помощью правил преобразования функций алгебры логики. Для этого условия работы схемы записываются в символической форме. Входные сигналы изображаются буквами, принятыми для обозначения двоичных переменных, а порядок преобразования информации в схеме как последовательность основных логических операций над двоичными переменными. Полученная логическая формула минимизируется, а затем каждая логическая операция заменяется соответствующим ей логическим элементом.

A	B	S	P
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Пример. Построить функциональную схему одноразрядного двоичного сумматора на два входа.

Такой сумматор принимает на входы разряды двоичных чисел А и В, складывает их, выдает разряд для суммы (S) и переноса (Р). На схеме показана логика работы сумматора. Из второй строки таблицы истинности видно, что при сложении 0 и 1 сумма равна единице (S=1), а перенос отсутствует (P=0). В виде формул логика работы сумматора выглядит так: . Проводя ряд тождественных преобразований, имеем: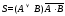. В результате получим схему, изображенную на рисунке.

Схема работы одноразрядного двоичного сумматора.

Построение логических схем по заданным функциям. В предыдущем примере логическая схема сумматора была построена по заранее известным формулам. Но иногда при проектировании (программировании) микросхемы компьютера требуется спроектировать тот или иной узел этой микросхемы на основании одного лишь словесного описания алгоритма логики его работы. Для решения такой проблемы проектировщик может поступить следующим образом:

1. на основании словесного алгоритма логики работы узла построить таблицу истинности для этого узла;

2. на основании таблицы истинности найти математическую формулу функционирования данного узла;

3. на основании формулы построить логическую схему функционирования данного узла.

Рассмотрим пример. Пусть в компьютере имеется логический узел Y с тремя входами А, В, С и одним выходом F(A, B, C). Логика работы узла Y следующая: если на входах единичных сигналов больше, чем нулевых, то функция F(A, В, С)=1, в остальных случаях F(A, В, С)=0. Построить логическую схему узла Y на базе элементов И, ИЛИ, НЕ.

Итак, нам известно, что узел Y имеет три входа и один выход, знаем словесное описание алгоритма работы данного узла, но мы не знаем, из чего узел должен состоять. То есть узел Y для нас - "черный ящик", в который надо заглянуть.

1. На основании словесного алгоритма логики работы узла Y строим таблицу истинности функции F. Поскольку функция трех переменных может принимать 2³ = 8 значений, то таблица истинности будет состоять из восьми строк.

2. На основании таблицы истинности находим математическую формулу функционирования узла Y. Воспользуемся описанным выше правилом построения СДНФ функции заданной этой таблицей истинности.

После упрощения получим:

или .

Для СКНФ в каждом произведении учитываются все простые высказывания тех строк таблицы, результирующее значение которых равно нулю. СКНФ будет иметь вид:

.

Эту функцию тоже можно подвергнуть процедуре упрощения.

3. На основании формулы строим логическую схему функционирования данного узла, используя формулы СДНФ.

Контрольное задание

1. В компьютере имеется логический узел Y с тремя входами А, В, С и одним выходом F(A,B,C). Логика работы узла Y следующая: если хотя бы на двух любых входах сигналы разные, то функция F(A,B,C) = 1. В остальных случаях F(A,B,C) = 0. Построить логическую схему узла Y на базе элементов И, ИЛИ, НЕ.