5.2.6. Взаимосвязь полных динамических характеристик иу

Как уже отмечалось, все полные динамические характеристики ИУ (ДХИУ) связаны друг с другом. В таблице 5.2 приведены основные формулы, описывающие эту связь.

Таблица 5.2.

Взаимосвязь полных динамических характеристик ИУ

ДХИУ
1	2	3	4	5	6

Для определения передаточной функции ИУ минимально-фазового типа , соответствующей заданной АЧХ, удобно пользоваться двумя соотношениями

и , (5.61)

где . Пусть, например, АЧХ ИУ имеет вид

.

Тогда, используя (5.61), получим

.

Определение дифференциального уравнения ИУ, соответствующего заданной передаточной функции , описано в разделе 5.2.2.1.

Таким образом, зная какую – либо полную динамическую характеристику ИУ, можно определить любую другую (полную или частную) динамическую характеристику этого ИУ.

5.3. Частные динамические характеристики иу

К частным динамическим характеристикам относятся числовые показатели динамической точности ИУ, характеризующие его способность реагировать на тестовые сигналы. Наиболее распространенными из них являются показатели качества переходного процесса и ширина полосы пропускания частот. Рассмотрим эти характеристики.

5.3.1. Длительность переходного процесса

В инерционных ИУ фактический переходный процесс всегда отличается от идеального переходного процесса (рис. 5.10), т.е. всегда имеет место переходная погрешность, которая с течением времени убывает (не обязательно монотонно). Для позиционных ИУ эта погрешность равна

, (5.62)

Определение:

Время , по истечении которого переходная погрешность не превышает допустимого значения этой погрешности, называется длительностью переходного процесса.

Используя данное определение, длительность переходного процесса (ДПП) можно определить графическим способом - как абсциссу точки, в которой относительная переходная характеристика ИУ последний раз пересекается с границами трубки точности 1  (см. рис. 5.10), или аналитическим способом - как максимальный положительный корень уравнения

, (5.63)

где - допустимое значение относительной переходной погрешности (5.62).

Рис. 5.10.

По истечении времени выполняется условие, т.е. переходная характеристика ИУцеликом заходит в трубку точности 1 . На рис. 5.11 показана схема соответствующего графического расчета ДПП.

Исходными данными для такого расчета являются передаточная функция ИУ W(p) и допустимая относительная переходная погрешность . В ходе расчета последовательно определяются операторная часть передаточной функции ИУ , изображение относительной переходной функциии соответствующий оригинал. Затем строится график относительной переходной функции, на который наносится трубка точности .Абсцисса точки последнего вхождения этого графика в трубку точности определяет искомую длительность переходного процесса .

Рис. 5.11.

Графический способ расчета ДПП оказывается неудобным в тех случаях, когда необходимо исследовать зависимость ДПП от одного или (тем более) нескольких параметров ИУ. В этих случаях вычисления, подобные показанным на рис. 5.11, приходится выполнять многократно для каждого значения варьируемого параметра ИУ, или сочетания таких параметров.

Более эффективным является другой (численный) способ расчета ДПП [26, 28]. В этом случае считается, что выражение для относительной переходной функции позиционного ИУ можно записать в виде

,

где - варьируемые коэффициенты передаточной функции ИУ. В общем случае такими коэффициентами являются коэффициентыдифференциального уравнения ИУ (5.1) зависящие от параметров ИУ.

Расчет ДПП, соответствующей заданному сочетанию коэффициентов , выполняется в Mathcad с использованием следующей процедуры - функции

.

Здесь - время, превышающее ожидаемое значение ДПП, - число, влияющее на точность расчета.

При обращении к этой функции интервал наблюдения разбивается наNT точек , где(рис. 5.12) и в каждой из них, начиная с точки , последовательно вычисляется значение модуля относительной переходной погрешности .

Рис. 5.12.

При нарушении условия , переменнойприсваивается величина. В результате осуществляется «продвижение» вдоль графика относительной переходной функции от точки(см. рис. 5.12) к точкеи по завершении расчетов определяется абсцисса точки первого выхода этого графика за границы трубки точности, т.е. находится ДПП, соответствующая заданному сочетанию значений варьируемых параметров передаточной функции ИУ. Точность расчета зависит от величины шагаи регулируется подбором числа- чем больше это число, тем выше точность расчета.

Описанная схема расчета является универсальной. Однако, в случае единичного определения ДПП проще пользоваться схемой графического расчета, показанной на рис. 5.11. В любом случае по завершение расчетов рекомендуется построить переходную характеристику ИУ и убедиться в том, что найденное значение ДПП является верным.

Из – за использования понятия «трубка точности» зависимость ДПП от параметров создаваемого ИУ может быть разрывной (см. Приложение 2, рис. П2.2) . Этот недостаток отсутствует, если время переходного процесса оценивать длительностью активной части этого процесса. В этом случае активной длительностью переходного процесса (АДПП) называется интервал времени , в котором сосредоточена основная часть энергии этого процесса. Такой интервал времени можно определить из уравнения

, (5.65)

где - соответственно энергия относительной переходной погрешности (5.62) на интервалеи полная энергия этой погрешности (на интервале), которые вычисляются по формулам (7.17) и (7.19) соответственно ; - постоянный коэффициент, определяющий долю полной энергии относительной переходной погрешности (5.62), приходящуюся на интервал времени, равный АДПП (например,).

В развернутой форме уравнение (5.65) имеет вид

. (5.66)

Интеграл в правой части этого уравнения совпадает с интегральной квадратичной оценкой переходного процесса (см. (5.67)). В разделе 5.3.2 показан способ вычисления этого интеграла.

Решая уравнение (5.66), можно для заданных ивычислить АДПП. В разделе П2.2.2 Приложения 2 показан пример такого расчета.

На рис. 5.13 показана типичная форма графика относительной переходной погрешности (для колебательного переходного процесса) и его активная длительность . Чем меньше коэффициентотличается от единицы, тем больше.

Рис. 5.13.

Если на график нанести трубку точности , то можно определить обычную ДПП. Чем меньше, тем больше. Для ИУ невысокого порядка значенияиблизки друг к другу в случае, если выполняется соотношение.

Недостатком АДПП является сложность экспериментального определения, достоинством – гладкая (непрерывная) зависимость от параметров ИУ.

5.3.2. Интегральные показатели качества переходного процесса

Длительность переходного процесса является не единственным показателем качества переходного процесса. Применяют другие, в частности интегральные оценки. Они вычисляются легче и, кроме того, позволяют одновременно добиться не только желаемой длительности переходного процесса, но еще и его желаемой формы.

Наиболее распространенными интегральными оценками качества переходного процесса являются интегральная квадратичная оценка (ИКОП)

. (5.67)

и обобщенная (улучшенная) интегральная квадратичная оценка (ОБИКОП).

, (5.68)

где - постоянная времени экстремального переходного процесса

. (5.69)

Подчиняя выбор параметров ИУ условию минимума этих оценок, определяют оптимальные параметры ИУ.

5.3.2.1. Интегральная квадратичная оценка переходного процесса

Из формулы (5.67) видно, что ИКОП является неотрицательной функцией тех параметров, которые влияют на относительную переходную функцию ИУ. Минимум ИКОПдостигается в случае идеального переходного процесса, при котором(см. рис. 5.10)). Поскольку строгое выполнение этого равенства невозможно, оптимальными считаются такие значения параметров ИУ, при которых соответствующее значение ИКОП минимально.

Для вычисления интеграла (5.67) нужно предварительно определить изображение по Лапласу относительной переходной погрешности (5.62)

. (5.70)

Поскольку рассматриваемые ИУ обладают дробно-рациональной передаточной функцией (5.7), изображение также является дробно-рациональным, т.е. имеет вид отношения полиномов

, (5.71)

где - постоянные коэффициенты, зависящие только от параметров ИУ.

ИКОП (5.67) зависит от значений этих коэффициентов и порядка передаточной функции ИУ. В частности:

1) Если и, то. (5.72)

2) Если и, то. (5.73)

3. Если и, то

и т.д. (5.74)

Если n > 3, то подобные формулы становятся громоздкими [20].

Пример 5.1. Покажем пример расчета ИКОП. Пусть передаточная функция ИУ имеет вид

.

Тогда ,,

где .

Следовательно .

Примечание: при вычислении изображения по формуле (5.70) нужно обращать внимание на строгое выполнение равенства, которое может нарушаться из - за округлений при расчетах. При правильных вычислениях также должно выполняться условие.

Применяя эти формулы, можно непосредственно связать значение ИКОП с параметрами ИУ и подчинить выбор этих параметров условию минимума ИКОП. В Приложении П2.2.5 показаны примеры такого расчета.

Стремление приблизить переходный процесс к идеальному скачку (за счет достижения минимального значения ИКОП) приводит к заметному перерегулированию и нежелательной колебательности оптимального переходного процесса. Для устранения этого недостатка применяют другие интегральные оценки качества переходного процесса, в частности обобщенную интегральную квадратичную оценку (5.68).

5.3.2.2. Обобщенная квадратичная интегральная оценка переходного процесса

Функционал (5.68) отличается от обычной ИКОП (5.67) наличием дополнительного слагаемого , величина которого тем больше, чем больше скорость переходного процесса. Поэтому условие минимума обобщенной квадратичной интегральной оценки переходного процесса

(ОБИКОП) снижает эту скорость на начальном участке переходного процесса. Благодаря этому устраняется отмеченный недостаток обычной ИКОП.

Глобальный минимум ОБИКОП достигается в случае, когда фактический переходный процесс совпадает с экстремальным переходным процессом (5.69), т.е. если. При выборе параметров ИУ по критерию минимума ОБИКОП всегда имеет место отклонение достигнутого минимального значения этой оценкиот ее глобального минимума, т.е. всегда имеет место разность. Соответствующий оптимальный переходный процессотличается от экстремального переходного процесса (5.69) на величину, не превышающую значения, то есть

. (5.75)

С ростом собственной частоты ИУ величинауменьшается. Поэтому, увеличивая, можно приближаться к экстремальному переходному процессу (5.69). Желаемое значение его длительностиможно обеспечить, выбирая необходимое значение постоянной времени экстремального переходного процесса. При этом можно руководствоваться приближенным соотношением. Чем выше, тем точнее выполняется это соотношение.

Из формулы (5.68) видно, что

,

где - обычная ИКОП;- интеграл, вычисляемый по формуле

. (5.76)

где - относительная весовая функция ИУ (см. (5.40)).

Отсюда следует, что ОБИКОП можно вычислять также как ИКОПи по тем же самым формулам (5.72) - (5.74). Только вместо изображения относительной переходной погрешности ИУ(5.70) в них нужно использовать операторную часть относительной передаточной функции ИУ.

5.3.3. Полоса пропускания частот

В инерционных ИУ всегда имеет место разница между графиками идеальной и фактической АЧХ, т.е. всегда имеет место частотная погрешность. Для позиционных ИУ она равна

. (5.77)

Определение:

Диапазон частот входного гармонического сигнала, в пределах которой частотная погрешность не превышает допустимого значения этой погрешности, называется полосой пропускания частот ИУ.

У позиционных ИУ такой диапазон занимает интервал частот (рис. 5.14), где- верхняя граница (ширина) полосы пропускания частот (ППЧ).

Ее значение можно определить графическим способом - как абсциссу точки первого выхода графика относительной АЧХ за границы трубки точности 1  , где - допустимое значение относительной частотной погрешности (см.рис. 5.14) илианалитическим способом – как минимальный положительный корень уравнений .

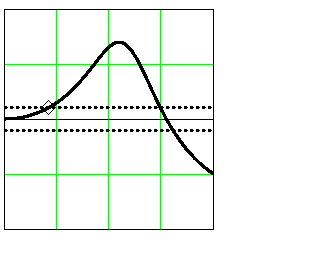
Рис. 5.14.

На рис. 5.15 показана схема графического расчета ширины ППЧ . Видно, что исходными данными для расчета являются передаточная функция ИУ W(p) и допустимое значение относительной частотной погрешности  . В ходе расчетов последовательно определяются операторная часть передаточной функции и относительная АЧХ ИУ. Затем строится график этой характеристики, на который наносится трубка точности 1 . Абсцисса точки первого выхода этого графика за границы трубки точности (при продвижении по графику слева направо от точки ) определяет верхнюю границу ППЧ(см. рис. 5.14).

Рис. 5.15.

В диапазоне частот выполняется условие. Поэтому в пределах этого диапазона частот ИУ оказывается «прозрачным» для гармонических сигналов, пропуская их так, что частотные искажения, обусловленные инерционностью элементов прибора, не превышают допустимого уровня.

Считается, что чем шире ППЧ, тем более совершенными являются динамические свойства ИУ. Это справедливо для регистрирующих ИУ, у которых относительная АЧХ в идеале должна совпадать с единичной ступенчатой функцией. Однако, в силу невозможности строгого выполнения этого условия, выбор параметров таких ИУ подчиняют условию максимума ширины ППЧ .

Графический способ расчета ППЧ оказывается неудобным в тех случаях, когда необходимо исследовать зависимость этого показателя динамической точности от одного или (тем более) нескольких параметров ИУ. В этих случаях расчет ППЧ, подобный изложенному выше, приходится выполнять многократно для каждого значения варьируемого параметра ИУ или сочетания таких параметров.

Возможен другой (более эффективный) способ численного расчета ППЧ в среде Mathcad [26,28]. В этом случае считается что относительная АЧХ позиционного ИУ имеет вид

, (5.78)

где - варьируемые коэффициенты передаточной функции ИУ, например коэффициенты дифференциального уравнения ИУ (5.1).

Расчет ширины ППЧ, соответствующей заданному сочетанию этих коэффициентов, можно выполнять с помощью процедуры – функции (5.79). Здесь - частота, превышающая ожидаемое значение ППЧ, - число, влияющее на точность расчета. При обращении к функции (5.79) интервал наблюдения разбивается наNW+1 точек (рис. 5.16) , гдеи в каждой из них последовательно вычисляется величина модуля относительной частотной погрешности.

(5.79)

Как только нарушается условие , результату вычислений присваивается значение переменной. В ходе вычислений осуществляется «продвижение» вдоль графика относительной АЧХ вправо от точкии определяется абсцисса точки первого выхода этого графика за границы «трубки точности», т.е. искомая верхняя граница полосы пропускания частотдля заданного сочетания варьируемых параметров ИУ (см. рис. 5.16) .

Рис. 5.16.

Точность расчета зависит от величины шага и регулируется изменением числа- чем больше это число, тем выше точность расчета. Если в результате расчета получено число, то следует увеличить ожидаемое максимальное значение ширины ППЧ.

Если , то форма АЧХ может значительно отличаться от показанной на рис. 5.16. В качестве примера таких ИУ рассмотрим виброметр (рис. 5.17)

Этот прибор предназначен для измерения и регистрации механических колебаний различных объектов: фундаментов, мостов, сооружений, земной коры и т.д. Вибрации объекта 1, на котором закреплен прибор, с помощью пружины 2 передаются инерционной массе 3. Благодаря этому изучение колебаний объекта «заменяется» изучением колебанийинерционной массы. С целью исключения влияния случайных толчков и ударов, колебания массы демпфируются демпфером4. Эти три элемента образуют сейсмическую систему прибора.

Рис. 5.17.

Передаточная функция сейсмической системы прибора , связывающая изображения по Лапласу регистрируемых колебаний основанияи колебаний инерционной массы, имеет вид

, (5.80)

где - соответственно масса груза, коэффициент демпфирования демпфера и жесткость пружины;- относительный коэффициент демпфирования и собственная частота сейсмической системы прибора. В этом случае.

На рис. 5.18, а показано семейство АЧХ рассматриваемого прибора для трех значений относительного коэффициента демпфирования ,и.

По оси абсцисс откладывается безразмерная относительная частота колебаний основания . Поэтому при увеличении собственной частоты прибораграфики сжимаются, а при уменьшении - растягиваются вдоль оси абсцисс, сохраняя свою форму. Накладывая на эти графики трубку точности, можно для каждого значенияопределить соответствующее относительное значение нижней границы полосы пропускания частот, как это показано на рис. 5.18,б для случая ,. В этом случае. Поэтому, если, то, т.е. прибор можно использовать для регистрации колебаний, частота которых превышает(4,9 Гц) .

а б

Рис. 5.18.

Из приведенных примеров видно различие в расчете ППЧ для квазистатических и дифференцирующих ИУ. В первом случае определяется верхняя граница ППЧ (как абсцисса точки первого выхода графика относительной АЧХ за границы трубки точности ), во втором - нижняя граница ППЧ (как абсцисса точки попадания этого графика в трубку точности).

В обоих случаях полоса пропускания частот ИУ должна превышать полосу частот измерительного сигнала. В противном случае динамические искажения этого сигнала, вызванные инерционностью элементов ИУ, превысят допустимую погрешность .

4. Оптимальные динамические характеристики ИУ

Вводя безразмерную комплексную переменную , относительную передаточную функцию линейных позиционных ИУ (5.12) можно записать в виде

, (5.81)

где - безразмерные постоянные коэффициенты, зависящие от параметров ИУ

, ; (5.82)

, ; (5.83)

- собственная частота ИУ. Например, для ИУ с передаточной функцией (5.20) имеем

,

.

Считается, что коэффициенты являются независимыми и управляемыми, т.е. поддаются изменениям. В противном случае получают не оптимальные, а квазиоптимальные динамические характеристики ИУ [30].

Для квазистатических ИУ . В этом случае

. (5.84)

Значения коэффициентов влияют на устойчивость собственных движений в приборе. Как отмечалось в разделе 5.2.2.1, они должны быть такими, чтобы корни характеристического уравнениярасполагались в левой полуплоскости комплексной переменной. Считается, что корни уравнениятакже располагаются в левой полуплоскости комплексной переменной, т.е. ИУ, рассматриваемые в данном разделе, относятся к классу устойчивых минимально-фазовых систем.

Значения коэффициентов ивлияют на форму относительной переходной функциии форму относительной частотной функции рассматриваемых ИУ. Согласно (5.24) и (5.58) эти функции можно определить по формулам

, , (5.85)

где - безразмерное время;- безразмерная частота . Затем можно вычислить числовые (частные) показатели динамической точности ИУ (длительность переходного процессаи ширину полосы пропускания частот) по формулам

, , (5.86)

где - относительные длительность переходного процесса и ширина полосы пропускания частот, зависящие от коэффициентовпередаточной функции ИУ (5.81) и величины допустимой динамической погрешности. Согласно (5.86) их значения совпадают с длительностью переходного процесса и, соответственно, - с шириной полосы пропускания частот ИУ, у которого.

В идеальном случае или. Поскольку строгое выполнение этих условий невозможно, оптимальными считаются такие значения параметров ИУ, при которых длительность переходного процесса минимальна или ширина полосы пропускания частот максимальна.

Выбор требований к динамическим характеристикам ИУ зависит от модели измерительного сигнала, назначения ИУ и режима его работы. Условие минимальной длительности переходного процесса обычно ставится при разработке приборов, предназначенных для измерения величин, не изменяющихся во времени, т.е., работающих в статическом режиме измерений. Если требуется измерять изменяющуюся во времени величину, то прибор должен обладать широкой полосой пропускания частот. В этом случае спектральные компоненты измерительного сигнала преобразуются без искажений.

Для снижения или увеличенияможно увеличивать собственную частоту ИУ. Если эта возможность ограничена, то можно, сохраняя, подобрать такие значения коэффициентовиотносительной передаточной функции ИУ (5.81), т.е. найти такую форму его динамических характеристик (5.85), при которой значениеминимально или значениемаксимально.

В лучшем случае эти требования выполняются, если характеристики или(в зависимости от критерия оптимальности) имеютпоочередных касаний с границами трубки точности, т.е. являются равноволновыми динамическими характеристиками порядка[27].

На рис. 5.19 показаны семейства таких характеристик для квазистатических ИУ порядков и случаев. Все графики в точках пиковых отклонений поочередно касаются верхней и нижней границ трубки точности. Если все коэффициентынезависимые, то число таких касаний должно быть на единицу меньше порядка передаточной функции ИУ, т.е. равно. Это условие является признаком оптимальности динамических характеристик ИУ.

Каждой кривой на рис. 5.19 соответствует определенное оптимальное сочетание значений коэффициентов передаточной функции квазистатического прибора (5.84), зависящее от порядка характеристического уравнения прибораи ширины трубки точности. В Приложении 3 даны значения этих коэффициентов, оптимизированные по критерию(таблица П3.1) и по критерию(таблица П3.2). Например, для кривой, показанной на рис. 5.19, а, . В этом случае. Для кривой, показанной на рис. 5.19, б, . В этом случае, т.е. квазистатические приборы, обладающие минимальной длительностью переходного процесса и максимальной шириной полосы пропускания частот, имеют разные значения параметров.

а) б)

Рис. 5.19. Оптимальные динамические характеристики квазистатического ИУ го порядка для случаеви: а – переходные характеристики , б – амплитудно-частотные характеристики.

С ростом значенияиувеличиваются. Поэтому для снижения длительности переходного процесса при проектировании квазистатических ИУ нужно стремиться к уменьшению, а для расширения полосы пропускания частот – к увеличению. С ростом допустимой динамической погрешности (или) значенияуменьшаются, а значения- увеличиваются.

В общем случае признак оптимальности динамических характеристик позиционных ИУ сохраняется, т.е. они также должны иметь последовательных касаний с границами трубки точности. Отличие заключается в том, что если, то, варьируя значениями коэффициентов передаточной функции ИУ (5.81), теоретически можно достичь сколь угодно малого значенияили сколь угодно большого значения. Поэтому наличие нулей у передаточной функции ИУ может значительно повысить его точность.

Рассмотрим позиционное ИУ второго порядка с передаточной функцией

. (5.87)

В этом случае условие выполняется, если коэффициентыисвязаны друг с другом соотношением

, (5.88)

где - относительная резонансная частота. Относительная АЧХ такого ИУв точке своего максимума (при) касается верхней границы трубки точности(подобно кривойна рис. 5.19,б). Соответствующее оптимальное значение определяется из уравнения, т.е. из уравнения

, (5.89)

где коэффициент вычисляется по формуле (5.88).

На рис. 5.20 сплошной кривой 1 показан график зависимости (5.88) для случая . Кривой 3 показана соответствующая (найденная из уравнения (5.89)) зависимость относительной ширины полосы пропускания частотот коэффициента. Видно, что при согласованном росте коэффициентови(учитывающим соотношение (5.88)) полоса пропускания частот ИУ монотонно возрастает.

Похожим соотношением связаны коэффициенты ипередаточной функции ИУ (5.87), если требуется выполнение условия(см. пунктирную кривую 2 на рис. 5.20). В этом случае переходный процесс в точке своего максимума касается верхней границы трубки точности, т.е. имеет форму кривой, показанной на рис. 5.19, а . Соответствующая зависимость отдля случаяна рис. 5.20 показана пунктирной кривой 4. Видно, что с ростом коэффициентовиотносительная длительность переходного процессамонотонно снижается.

Рис. 5.20. К расчету оптимальных значений параметров передаточной функции ИУ видадля случая: 1,3 – по критерию ; 2,4 – по критерию

Таким образом, оптимальными динамическими характеристиками линейных позиционных ИУ го порядка являются равноволновые динамические характеристики порядка. При этом наличие у передаточной функции нулей может существенно улучшить динамические характеристики ИУ.

Расчет свободных (независимых) коэффициентовотносительной передаточной функции ИУ (5.81), оптимизированных по критерию, сводится к решению системыалгебраических уравнений относительнонеизвестных величин:изискомых коэффициентовиабсциссточек экстремумов относительной переходной погрешности, в которых она последовательно достигает своих предельных значений

,

, (5.90)

где ;- производная. Аналогично, для расчетасвободных коэффициентов, оптимизированных по критерию, нужно найти решение системыалгебраических уравнений

,

, (5.91)

где ;- производная;абсциссы точек экстремумов относительной частотной погрешности, в которых она последовательно достигает своих предельных значений.

Если коэффициенты известны, то каждому сочетанию этих коэффициентов соответствует определенное оптимальное сочетание коэффициентов.

На практике число свободных коэффициентов передаточной функции ИУ (5.81) может быть ограничено. В этом случае число касаний наилучших динамических характеристик ИУ (5.85) с границами трубки точности снижается. Такие динамические характеристики называются квазиоптимальными [30].

Для решения систем уравнений (5.90) и (5.91) удобно использовать программу MATHCAD [26]. В таблице П3.3 даны полученные с помощью этой программы оптимальные сочетания значений коэффициентов относительной передаточной функции прибора (5.87) для случая.

Если , то передаточная функция прибора (5.87) становится эквивалентной передаточной функции колебательного звена. В этом случае существуют точные формулы, позволяющие вычислить оптимальное значение коэффициента[6]: если требуется выполнить условие, то (см. (П2.20))

, (5.92)

если нужно обеспечить минимальное значение , то (см. (П2.11))

. (5.93)

На рис. 5.20 этим значениям коэффициента соответствуют точки пересечений кривых 3,4 с осью ординат.

При увеличении порядка характеристического уравнения прибора увеличивается число оптимизируемых коэффициентов его передаточной функции (5.81). В таблице П3.4 даны сочетания значений этих коэффициентов для прибора с передаточной функцией

(5.94)

и случаев .

Если , то условием оптимальности динамических характеристик ИУ являются равенства. В этом случае,,.

Для определения оптимальных значений коэффициентов передаточной функции прибора можно использовать разложение относительной операционной погрешности в ряд по степеням[3,4]. В этом случае

. (5.95)

Переходная погрешность отсутствует, если

, ,, … . (5.96)

Выполнение этих условий возможно не для всех членов ряда (5.95), а только лишь для числа членов, равного числу искомых коэффициентов передаточной функции прибора. При этом существенное значение имеет, какие именно члены этого ряда принимаются во внимание. Поэтому решение задачи получают методом последовательных приближений.

Если целью синтеза является расширение полосы пропускания частот, то условия оптимальности получают, приравнивая нулю коэффициенты разложения

, (5.97)

где - квадрат относительной АЧХ. В этом случае решение также оказывается приближенным.

Изложенное выше относится к невозмущенному режиму измерений, при котором отсутствуют помехи и все параметры ИУ сохраняют свои номинальные значения. Возникающая при этом погрешность измерений называется собственной динамической погрешностью ИУ. При наличии помех может оказаться полезным сокращение полосы пропускания частот ИУ. В этом случае динамические характеристики ИУ должны быть согласованы не только с характеристиками полезного сигнала, но и с характеристиками помех. Необходимость в таком согласовании характеристик обнаруживается при анализе суммарной погрешности измерений (см. раздел 9.2.5).

Контрольные вопросы

1. Поясните назначение и состав динамических характеристик ИУ.

2. Напишите дифференциальное уравнение линейного стационарного ИУ го порядка. Приведите пример такого уравнения.

3. Дайте определение понятия «передаточная функция ИУ». Какова размерность передаточной функции ?

4. Поясните связь передаточной функции с дифференциальным уравнением и статической характеристикой ИУ. Какие ИУ называются квазистатическими, дифференцирующими, позиционными? Приведите примеры таких ИУ.

5. Поясните порядок расчета передаточной функции ИУ (имеющего известную структурную схему) поэтапным методом, методом структурных преобразований и методом исключения промежуточных переменных. Приведите примеры такого расчета (Приложение 5, задача 5.1).

6. Дайте определение понятий «переходная функция ИУ» и «переходная характеристика ИУ». Чем отличаются эти понятия ?

7. Определите переходную функцию ИУ, имеющего известную передаточную функцию . Используя полученный результат, поясните свойства переходной функции ИУ.

8. Дайте определение понятия «весовая (импульсная переходная) функция ИУ». Определите весовую функцию ИУ, имеющего известную передаточную функцию . Используя полученный результат, поясните свойства весовой функции ИУ.

9. Поясните физический смысл амплитудно-частотной, фазо-частотной и амплитудно – фазовой характеристик ИУ.

10. Напишите формулы, связывающие друг с другом полные динамические характеристики ИУ. Определите эти характеристики для прибора, имеющего известную переходную функцию .

11. Поясните физический смысл понятия «длительность переходного процесса». Каков порядок аналитического, графического и численного расчета длительности переходного процесса. Приведите пример такого расчета (Приложение 5, задача 5.2).

12. Поясните физический смысл понятия «активная длительность переходного процесса». Каковы достоинства и недостатки этого показателя динамической точности ИУ?

13. Поясните цель и порядок расчета интегральных показателей качества переходного процесса. Приведите пример такого расчета (Приложение 5, задача 5.4).

14. Поясните физический смысл понятия «ширина полосы пропускания частот». Каков порядок аналитического, графического и численного расчета полосы пропускания частот. Приведите пример такого расчета (Приложение 5, задача 5.3).

15. Поясните отличие расчета полосы пропускания частот для сейсмических и квазистатических приборов.

16. Сформулируйте условия оптимальности динамических характеристик позиционного ИУ ого порядка.