4.4. Расчет погрешности от нелинейности статической характеристики иу

Нелинейность статической характеристики ИУ выражается в наличии отклонений этой характеристики от аппроксимирующей прямой. В качестве такой прямой используют хорду (рис. 4.8,а), касательную (в выбранной точке), прямую наименьших модулей (рис. 4.8, б) или прямую наименьших квадратов (рис. 4.8, в).

Хордой называется прямая, соединяющая граничные точки статической характеристики ИУ. Прямой наименьших модулей (ПНМ) называется прямая, максимальное отклонение которой от статической характеристики ИУ является минимальным. Это условие выполняется, если пиковые отклонения ПНМ от кривой равны друг другу по величине, т.е. (для рис. 4.8, б) . Прямой наименьших квадратов (ПНК) называется прямая отклонения которой от статической характеристики ИУ являются малыми в области наиболее вероятных значений измеряемой величины, т.е. там, где значения плотности распределения вероятностей максимальны (рис. 4.8,в). В случае равномерного закона распределения измеряемой величины ПНМ и ПНК близки друг к другу.

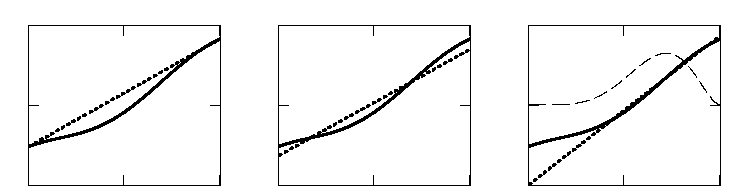
Рис. 4.8.

Основным способом устранения погрешности от нелинейности является подбор (на практике подгонка) статических характеристик звеньев прибора или включение в его схему специального (корректирующего) звена с нужной статической характеристикой. В современных приборах эта погрешность устраняется алгоритмическим способом. В этом случае прибор содержит программируемое вычислительное устройство (микроконтроллер), в котором реализуется необходимый алгоритм вычисления результата измерений, учитывающий нелинейность статической характеристики аналоговой части прибора.

4.4.1. Расчет прямой наименьших модулей и максимальной приведенной

погрешности от нелинейности статической характеристики ИУ

Определение: Прямой наименьших модулей (по отношению к кривой ) называется прямая, максимальное отклонение которой от кривойна отрезкеявляется минимальным.

Параметры такой прямой определяются из условия минимума неявно заданной функции двух переменных, выражающей максимальное на отрезке отклонение прямой от кривой, т.е. из условия

, где . (4.27)

Те значения аргументов функции , при которых выполняется это условие, являются параметрами прямой наименьших модулей. Соответствующаямаксимальная приведенная погрешность от нелинейности (МППН) вычисляется по формуле

, (4.28)

где - максимальное отклонение ПНМ от статической характеристики ИУ;- граничные ординаты ПНМ (,).

Условие (4.27), называемое критерием минимакса, равносильно условиям равномерного приближения функций ина отрезке. Их можно записать в виде системынелинейных алгебраических уравнений

, , (4.29)

где - пиковые значения модуля абсолютной погрешности приближения

, (4.30)

число которых зависит от особенностей приближаемой функции;() - абсциссы точек экстремумов погрешности приближения (4.30), числокоторых также зависит от особенностей этой функции.

Решая систему уравнений (4.29), находят параметры ПНМ и, кроме того, абсциссы точек экстремумов погрешности приближения (4.30). После этого можно вычислить максимальные значения модуля этой погрешности. Все они должны быть равны друг другу, т.е. должны выполняться равенства

. (4.31)

В этом случае статическая характеристика ИУ оказывается заключенной между двумя параллельными прямыми, отстоящими от графика ПНМ на одинаковую величину.

Таких вариантов может быть несколько. На рис. 4.9 в качестве примера показаны два таких варианта. Они отличаются разным числом переходов кривой с одной прямой на другуюи разными значениями чисели. Для первого варианта (при котором кривая ограничена сплошными параллельными прямыми 1) имеем,и. Для второго варианта (при котором кривая ограничена штрихпунктирными параллельными прямыми 2),и. Чем больше число, тем меньше.

Прямую наименьших модулей можно построить графическим способом. Для этого нужно провести две параллельные прямые так, чтобы кривая оказалась заключенной между ними, а число переходовэтой кривой с одной прямой на другую было максимально возможным. Прямая, проходящая посредине между этими прямыми есть ПНМ [30].

Из рис. 4.9 видно, что не обязательно все экстремумы погрешности приближения (4.30) должны быть равны друг другу по величине. Число таких экстремумов , как уже отмечалось, зависит от особенностей приближаемой функции. Этим объясняется неоднозначность выбора условий равномерного приближения (4.29) для графика сложной функции и необходимость поискаглобального минимума функции (4.26).

Рис. 4.9.

В практических приложениях выбор уравнения ПНМ выполняют с учетом следующих рекомендаций:

1) если и, то принимают, т.е. считают, что(рис. 4.10,а), хотя расчет в этом случае дает завышенное значение погрешности. При этом исходят из правила – если на входе прибора ничего нет, то на его выходе сигнал также должен отсутствовать;

2) если , т.е. статическая характеристика ИУ нечетная и, кроме того,, то также принимают(рис. 4.10,б).

Во всех остальных случаях принимают (рис. 4.10,в).

В любом случае исходными данными для расчета являются функция преобразования ИУ и пределы диапазона измерений (), а результатами расчета – параметры ПНМи значение МППН. Покажем пример такого расчета.

в

Рис. 4.10.

Пример 4.4. Определить ПНМ и МППН для статической характеристики , заданной на интервале(т.е.,).

Решение: На рис. 4.8, б показан график такой характеристики. В этом случае условия равномерного приближения (4.29) образуют систему четырех уравнений (см. рис. 4.8, б)

, ,,,

где ,,

, ,.

Решая эту систему уравнений, получим ,,,, т.е. уравнение ПНМ имеет вид.

На рис. 4.11, а показано соответствующее распределение погрешности приближения (4.30) по диапазону измерений, на рис. 4.11,б - карта линий уровней функции в окрестности точки минимума. Параметрыкоординаты этой точки.

Видно, что условия равномерного приближения (4.29) выполняются. Максимальное значение погрешности приближения равно . Соответствующее значение МППН (4.28) равно.

Таким образом, расчет параметров ПНМ можно выполнять двумя способами:

1) путем решения системы уравнений (4.29);

2) путем определения координат точки глобального минимума неявно заданной функции двух переменных (4.27). На практике обе эти возможности применяются вместе, взаимно дополняя друг друга [28].

а б

Рис. 4.11.

4.4.2. Расчет прямой наименьших квадратов и среднеквадратической приведенной

погрешности от нелинейности статической характеристики ИУ

Оценку нелинейности статической характеристики ИУ в форме МППН рекомендуется применять в тех случаях, когда погрешность приближения (4.30) ни в одной точке диапазона измерений не должна превышать допустимого значения. Часто это требование можно заменить менее жестким требованием - погрешность (4.30) может оказаться «большой», но это должно происходить «редко». В этом случае принимается во внимание тот факт, что измеряемая физическая величина , будучи случайной величиной, с разной вероятностью попадает в разные части диапазона измерений . Эта вероятность пропорциональна значениям функции плотности распределения вероятностей измеряемой величины(ПРВ), характеризующей статистические свойства измеряемой величины. Поэтому отклонения статической характеристики ИУ от аппроксимирующей прямой должны быть малыми в той части диапазона измерений, где значения ПРВ близки к максимуму и могут быть большими там, где эти значения незначительные. В результатемалые значения погрешности приближения оказываются более вероятными (см. рис. 4.8, б). Таким свойством обладает прямая наименьших квадратов (ПНК).

Определение: Прямой наименьших квадратов (по отношению к кривой ) называется прямая, среднеквадратическое отклонение которой от кривойна отрезкеявляется минимальным.

Параметры ПНК определяются из условия минимума математического ожидания квадрата погрешности приближения (4.30), т.е. из условия

. (4.32)

Приравнивая нулю производные этой функции по ии решая полученную систему уравнений, можно получить следующие формулы

, , (4.33)

где - определенные интегралы, зависящие от формы ПРВи формы статической характеристики ИУ

, ,

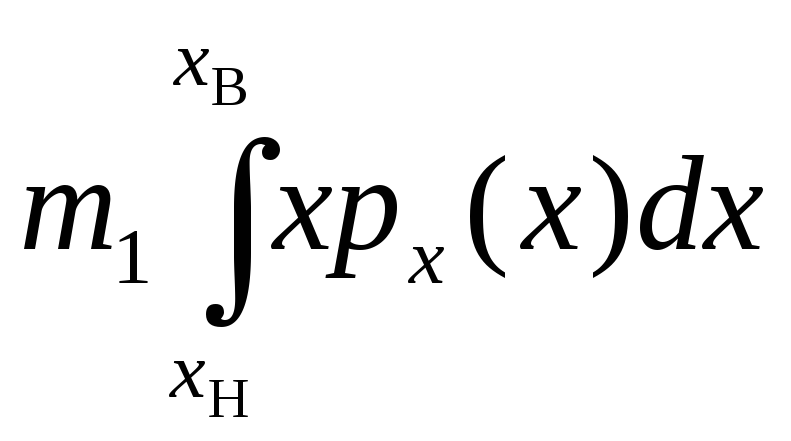, ,. (4.34)

Соответствующее минимальное значение функции равно

, где . (4.35)

Если все значения измеряемой величины находятся внутри интервала , то в этих формулах нужно принять.

При выборе уравнения ПНК руководствуются теми же правилами, что и при выборе уравнения ПНМ (см. рис. 4.10), т.е. это уравнение может быть «полным» , или «усеченным». В первом случае расчет параметров ПНК выполняется по формулам (4.33). Если, то коэффициент наклона ПНКи величинавычисляются по другим формулам

. (4.36)

. (4.37)

В этом случае расчет дает завышенное значение погрешности.

Если параметры ПНК вычисляются по формулам (4.33), то математическое ожидание погрешности приближения (4.30) равно нулю, т.е.

. (4.38)

В этом случае интеграл (4.32) совпадает с дисперсией погрешности приближения (4.30).

Степень близости ПНК к статической характеристике ИУ оценивается по величине среднеквадратической приведенной погрешности от нелинейности (СППН)

. (4.39)

Чем меньше , тем меньше нелинейность статической характеристики ИУ.

Покажем пример такого расчета.

Пример 4.5. Определить ПНК и СППН для статической характеристики ИУ , показанной на рис. 4.8, в.

Решение: Кривая , показанная на рис. 4.8,в задана на интервале (т.е.,) и имеет уравнение, а плотность распределения вероятностей – уравнение,

где - постоянный коэффициент, обеспечивающий выполнение условия нормировки ПРВ (7.73).

По формулам (4.33) и (4.34) для этого случая находим ,. Соответствующее минимальное значение дисперсии погрешности приближения (4.35) равно, а значение СППН (4.39) равно.

На рис. 4.12, а сплошной кривой показано распределение погрешности приближения по диапазону измерений. Пунктирная криваяпоказывает распределения вероятностей значений измеряемой величины(график ПРВ). Видно, что в правой части диапазона измерений, где значения ПРВ велики, погрешность приближения снижена. На рис. 4.12,б показана карта линий уровней функции . Видно наличие точки минимума. Параметрыкоординаты этой точки.

а б

Рис. 4.12.

4.4.3. Свойства погрешности от нелинейности статической характеристики ИУ

Функция в точке своего минимума является недифференцируемой функцией. Функция , напротив, является гладкой. На рис. 4.13 показаны типичные формы графиков этих функций в окрестности точки минимума.

а б

Рис. 4.13.

Кроме этой особенности, погрешность от нелинейности обладает свойствами, зная которые, можно значительно упростить расчет этой погрешности. Укажем на них [28]. Для этого приведенную погрешность от нелинейности статической характеристики ИУ , заданной на интервале, обозначим, понимая под этим обозначением как максимальную, так и среднеквадратическуюпогрешности .

Тогда:

1. Если , то, (4.40)

т.е. умножение статической характеристики ИУ на постоянный коэффициентне влияет на значение приведенной погрешности от нелинейности этой характеристики.

2. Если , то, (4.41)

т.е. смещение статической характеристики ИУ вдоль оси ординат не влияет на значение приведенной погрешности от нелинейности этой характеристики.

3. Свойство 3 является следствием объединения свойств 1 и 2 и формулируется следующим образом:

Если , то, (4.42)

т.е. линейное преобразование статической характеристики ИУ приводит к новой характеристике, имеющей то же значение приведенной погрешности от нелинейности.

4. Если , то, (4.43)

т.е. изменение масштаба входного сигнала не изменяет значение приведенной погрешности от нелинейности этой характеристики.

5. Если, то, (4.44)

т.е. смещение статической характеристики ИУ вдоль оси абсцисс не изменяет значение приведенной погрешности от нелинейности этой характеристики.

6. Свойство 6 является следствием объединения свойств 4 и 5 и формулируется следующим образом:

Если , то, (4.45)

т.е. линейное преобразование аргумента функции преобразования не изменяет значение приведенной погрешности от нелинейности статической характеристики ИУ.

7. Приведенные погрешности от нелинейности прямой (4.1) и обратной (4.2) статических характеристик ИУ равны друг другу, т.е.

. (4.46)

Если - максимальная приведенная погрешность и, то равенство (4.46) выполняется строго, если же- среднеквадратическая приведенная погрешность, то, вследствие деформации закона распределения измеряемой величины, это равенство выполняется с приближением, которым на практике обычно можно пренебречь

По аналогии с (7.14) будем считать, что две статические характеристики иимеютодинаковую форму, если существуют такие вещественные числа , при которых выполняется равенство

. (4.47)

Тогда, объединяя все перечисленные свойства, можно утверждать : два ИУ имеют одинаковое значение приведенной погрешности от нелинейности, если статические характеристики этих ИУ имеют одинаковую форму.