
- •Преобразование Лапласа и его свойства
- •Преобразования Лапласа простых функций.
- •Динамические характеристики типовых иу
- •Динамические характеристики типовых иу первого порядка
- •Полные динамические характеристики типовых иу второго порядка
- •Уравнения границ областей диаграммы Вышнеградского
- •Уравнения границ областей частотной диаграммы
- •Оптимальные сочетания значений коэффициентов относительной передаточной функции иу для случаев .
- •Оптимальные сочетания значений коэффициентов относительной передаточной функции прибора для случая
- •П5.1. Задачи к главе 3 «Разработка математической модели иу»
- •Экспериментальные данные
- •2. Предложенных мероприятий достаточно для снижения суммарной погрешности прибора до заданного уровня 0,5%.
Полные динамические характеристики типовых иу второго порядка
|
№ |
Динамическая характеристика |
Формула |
|
1 |
Дифференциальное уравнение
|
|
|
2 |
Относительная передаточная функция |
|
|
3 |
Относительная переходная функция |
где
|
|
4 |
Относительная весовая функция |
|
|
5 |
Относительная амплитудная частотная функция |
где
|
|
Фазовая частотная функция |
|
Анализ приведенных данных позволяет сделать следующие выводы:
-
Собственная частота ИУ
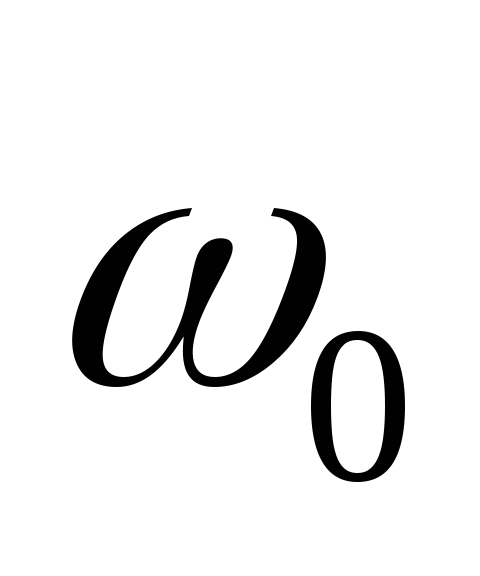 не влияет на форму переходного процесса
и форму АЧХ. При увеличении
не влияет на форму переходного процесса
и форму АЧХ. При увеличении
 переходная характеристика ИУ
переходная характеристика ИУ
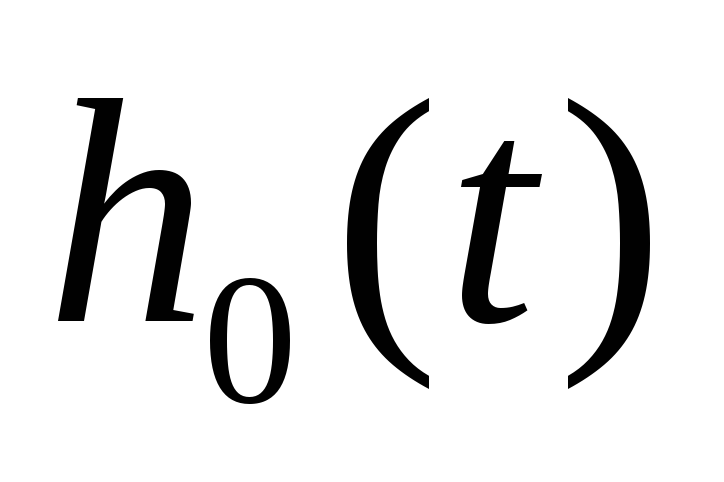 сжимается, а при уменьшении – растягивается
вдоль оси абсцисс, сохраняя свою форму.
АЧХ
сжимается, а при уменьшении – растягивается
вдоль оси абсцисс, сохраняя свою форму.
АЧХ
 ,
наоборот, при увеличении
,
наоборот, при увеличении
 растягивается, а при уменьшении
растягивается, а при уменьшении
 – сжимается, также сохраняя свою форму.
– сжимается, также сохраняя свою форму.
-
Относительный коэффициент демпфирования
 ,
напротив, существенно влияет на форму
переходного процесса и форму АЧХ.
,
напротив, существенно влияет на форму
переходного процесса и форму АЧХ.
Это влияние демонстрируется графиками, показанными на рис. П2.1.


а б в г д е
Рис. П2.1
Переходный процесс
колебательный, если
![]() и монотонный, если
и монотонный, если
![]() .
Существует такое значение относительного
коэффициента демпфирования
.
Существует такое значение относительного
коэффициента демпфирования
![]() ,
при котором переходная характеристика
ИУ в точке своего максимума касается
верхней границы трубки точности
,
при котором переходная характеристика
ИУ в точке своего максимума касается
верхней границы трубки точности
![]() (см. рис. П2.1, б).
В этом случае относительная длительность
переходного процесса
(см. рис. П2.1, б).
В этом случае относительная длительность
переходного процесса
![]() минимальна т.е.
минимальна т.е.
![]() .
.
АЧХ пологая, если
![]() ,
и одногорбая резонансная, если
,
и одногорбая резонансная, если
![]() .
Существует также такое значение
.
Существует также такое значение
![]() , при котором АЧХ в точке своего максимума
касается верхней границы трубки точности
, при котором АЧХ в точке своего максимума
касается верхней границы трубки точности
![]() (см. рис. П2.1, д).
В этом случае относительная ширина
полосы пропускания частот
(см. рис. П2.1, д).
В этом случае относительная ширина
полосы пропускания частот
![]() максимальна т.е.
максимальна т.е.
![]() .
.
П2.2.1. Длительность переходного процесса
Длительность
переходного процесса
![]() вычисляется по формуле
вычисляется по формуле
![]() ,
(П2.6)
,
(П2.6)
где
![]() -
безразмерная относительная ДПП, зависящая
только от
-
безразмерная относительная ДПП, зависящая
только от
![]() и
и
![]() .
.
Для вычисления
![]() нужно, полагая
нужно, полагая
![]() ,
построить график относительной
переходной функции ИУ
,
построить график относительной
переходной функции ИУ
![]() ,
соответствующий заданному значению
,
соответствующий заданному значению
![]() (см формулы п. 3 таблицы П2.2), и, наложив
на него трубку точности
(см формулы п. 3 таблицы П2.2), и, наложив
на него трубку точности
![]() ,
определить такое значение
,
определить такое значение
![]() ,
при котором этот график последний раз
пересекается с границами трубки точности
,
при котором этот график последний раз
пересекается с границами трубки точности
![]() (см.
рис. 5.10). Найденное значение
(см.
рис. 5.10). Найденное значение
![]() равно
равно
![]() .
.
Приближенное
значение относительной длительности
переходного процесса
![]() можно вычислить по формулам, вид которых
зависит от значения относительного
коэффициента демпфирования
можно вычислить по формулам, вид которых
зависит от значения относительного
коэффициента демпфирования
![]() :
:
-
Если
 ,
то
,
то
 ,
(П2.7)
,
(П2.7)
-
если
 ,
то
,
то
 , (П2.8)
, (П2.8)
-
если
 ,
то
,
то
 ,
(П2.9)
,
(П2.9)
-
если
 ,
то
,
то
 .
(П2.10)
.
(П2.10)
В этих формулах используются следующие обозначения:
![]() ;
(П2.11)
;
(П2.11)
![]() ,
(П2.12)
,
(П2.12)
где
![]() -
порядковый номер первого экстремума
относительной переходной характеристики
ИУ, не выходящего за границы трубки
точности
-
порядковый номер первого экстремума
относительной переходной характеристики
ИУ, не выходящего за границы трубки
точности
![]() .
Его можно вычислить по формуле
.
Его можно вычислить по формуле
![]() ,
(П2.13)
,
(П2.13)
где
![]() означает округление величины
означает округление величины
![]() в большую сторону до получения целого
числа (например,
в большую сторону до получения целого
числа (например,
![]() ,
,
![]() и т.д., для графика на рис. 5.10
и т.д., для графика на рис. 5.10
![]() )
;
)
;
![]() - минимальная относительная ДПП,
приближенное значение которой можно
вычислять по формуле (П2.7), где в этом
случае нужно принять
- минимальная относительная ДПП,
приближенное значение которой можно
вычислять по формуле (П2.7), где в этом
случае нужно принять
![]() и
и
![]() .
.
На рис. П2.2 показан
типичный график зависимости
![]() от
от
![]() .
Величина
.
Величина
![]() минимальна при определенном оптимальном
значении относительного коэффициента
демпфирования
минимальна при определенном оптимальном
значении относительного коэффициента
демпфирования
![]() ,
зависящем от
,
зависящем от
![]() (см. (П2.11)).
(см. (П2.11)).


Рис. П2.2.
Соответствующая
относительная переходная характеристика
ИУ показана на рис. П2.3 (кривая 1). В точке
максимума она касается верхней границы
трубки точности
![]() . Если
. Если
![]() ,
то максимум переходной характеристики
выходит за границу
,
то максимум переходной характеристики
выходит за границу
![]() трубки точности (см. кривую 2 на рис.
П2.3), и напротив, если
трубки точности (см. кривую 2 на рис.
П2.3), и напротив, если
![]() ,
то он находится внутри этой трубки (см.
кривую 3 на рис. П2.3).
,
то он находится внутри этой трубки (см.
кривую 3 на рис. П2.3).


Рис. П2.3.
В обоих случаях
точки
![]() и
и
![]() ,
в которых переходная характеристику
ИУ последний раз пересекается с границами
трубки точности, смещаются вправо, т.е.
величина
,
в которых переходная характеристику
ИУ последний раз пересекается с границами
трубки точности, смещаются вправо, т.е.
величина
![]() увеличивается.
увеличивается.
В точках
![]() ,
где
,
где
![]() .
(П2.14)
.
(П2.14)
зависимость
![]() от
от
![]() имеет разрывы первого рода (см. рис.
П2.2). В этих случаях переходная
характеристика ИУ в точках
имеет разрывы первого рода (см. рис.
П2.2). В этих случаях переходная
характеристика ИУ в точках
![]() касается границы
касается границы
![]() трубки точности (рис. П2.4). Поэтому
условие
трубки точности (рис. П2.4). Поэтому
условие
![]() приводит к скачкообразному увеличению
приводит к скачкообразному увеличению
![]() .
.
![]()
![]()

![]()
![]()
![]()


![]()
![]()
![]()
![]()



![]()

Рис. П2.4.
П2.2.2. Активная длительность переходного процесса
Активная длительность
переходного процесса (АДПП)
![]() определяется из уравнения (5.66). Для
типового ИУ второго порядка это уравнение
приводится к виду
определяется из уравнения (5.66). Для
типового ИУ второго порядка это уравнение
приводится к виду
![]()
(П2.15)
где
![]() ,
,
![]() - относительная АДПП. Решая это уравнение,
можно для заданных значений
- относительная АДПП. Решая это уравнение,
можно для заданных значений
![]() и
и
![]() определить
определить
![]() .
.
Расчет обычной
ДПП
![]() и активной ДПП
и активной ДПП
![]() дает близкие результаты, если величины
дает близкие результаты, если величины
![]() и
и
![]() связаны друг с другом соотношением
(П2.5). На рис. П2.5, а
показаны графики зависимости
связаны друг с другом соотношением
(П2.5). На рис. П2.5, а
показаны графики зависимости
![]() от
от
![]() для трех значений
для трех значений
![]() :
:
![]() ,
,
![]() и
и
![]() ,
на рис. П2.5, б
– графики
зависимости
,
на рис. П2.5, б
– графики
зависимости
![]() от
от
![]() для трех соответствующих (вычисленных
по формуле (П2.5)) значений коэффициента
для трех соответствующих (вычисленных
по формуле (П2.5)) значений коэффициента
![]() :
:
![]() ,
,
![]() и
и
![]() .
.

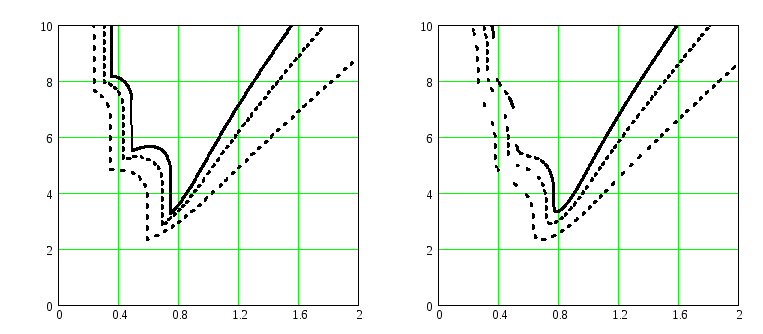
а б
Рис. П2.5.
П2.2.3. Перерегулирование
Перерегулирование
![]() характеризует максимальное отклонение
относительной переходной характеристики
ИУ от установившегося единичного уровня.
В типовом ИУ второго порядка
перерегулирование зависит только от
значения относительного коэффициента
демпфирования
характеризует максимальное отклонение
относительной переходной характеристики
ИУ от установившегося единичного уровня.
В типовом ИУ второго порядка
перерегулирование зависит только от
значения относительного коэффициента
демпфирования
![]() и вычисляется по формуле
и вычисляется по формуле
![]() .
(П2.16)
.
(П2.16)
С ростом
![]() перерегулирование монотонно уменьшается
вплоть до значения
перерегулирование монотонно уменьшается
вплоть до значения
![]() при
при
![]() .
Если
.
Если
![]() ,
то равенство
,
то равенство
![]() сохраняется, так как в этом случае
переходный процесс становится монотонным.
сохраняется, так как в этом случае
переходный процесс становится монотонным.
Если
![]() ,
то переходный процесс является
колебательным. На рис. П2.6 показаны
характерные точки соответствующей
относительной переходной характеристики
ИУ
,
то переходный процесс является
колебательным. На рис. П2.6 показаны
характерные точки соответствующей
относительной переходной характеристики
ИУ
![]() ,
где
,
где
![]() .
(П2.17)
.
(П2.17)
Такими точками
являются: точки экстремумов
![]() ,
точки пересечения графика с установившимся
единичным уровнем
,
точки пересечения графика с установившимся
единичным уровнем
![]() и две точки
и две точки
![]() ,
,![]() на переднем фронте переходного процесса.
на переднем фронте переходного процесса.
![]()
![]()


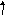





![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()




![]()
![]()
![]()
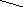

![]()
![]()
![]()

Рис. П2.6.
Координаты всех
этих точек можно вычислить (зная только
значение
![]() )
по формулам:
)
по формулам:
- абсциссы точек
экстремумов:
![]() ,
где
,
где
![]() ,
,
![]() ;
;
- ординаты точек
экстремумов:
![]() ;
;
-
абсциссы точек пересечений с единичным
уровнем
![]() ;
;
-
пиковые отклонения от единичного уровня
![]() ;
;
-
координаты точки A:
![]() ,
,
![]() ;
;
-
координаты точки B:
![]() ,
,
![]() .
.
С
помощью этих формул несложно вручную
построить переходную характеристику
типового ИУ второго порядка, соответствующую
заданному значению относительного
коэффициента демпфирования
![]() .
.
П2.2.4. Частотные динамические характеристики
На рис. П2.7, а
показано семейство АЧХ, на рис. П2.7, б
- семейство ФЧХ, на рис. П2.7, в
- семейство АФЧХ типового ИУ второго
порядка. Все графики соответствуют
единичному значению собственной частоты
ИУ
![]() и трем различным значениям относительного
коэффициента демпфирования
и трем различным значениям относительного
коэффициента демпфирования
![]() ,
,
![]() и
и
![]() .
Если
.
Если
![]() ,
то АЧХ имеет резонансный пик, причем,
чем меньше
,
то АЧХ имеет резонансный пик, причем,
чем меньше
![]() ,
тем этот пик острее. Точка максимума
АЧХ соответствует резонансной частоте
,
тем этот пик острее. Точка максимума
АЧХ соответствует резонансной частоте
![]() .
Соответствующее максимальное значение
относительной амплитуды установившегося
выходного сигнала равно
.
Соответствующее максимальное значение
относительной амплитуды установившегося
выходного сигнала равно
![]() .
.



а б в
Рис. П2.7.
Ширина полосы пропускания частот (ППЧ) типового ИУ второго порядка вычисляется по формуле
![]() ,
(П2.18)
,
(П2.18)
где
![]() -
безразмерная относительная ширина ППЧ,
зависящая только от
-
безразмерная относительная ширина ППЧ,
зависящая только от
![]() и
и
![]() .
Из формулы (П2.18) следует, что величина
.
Из формулы (П2.18) следует, что величина
![]() (для заданных значений
(для заданных значений
![]() и
и
![]() )
совпадает с шириной ППЧ типового ИУ
второго порядка, у которого собственная
частота равна единице, т.е.
)
совпадает с шириной ППЧ типового ИУ
второго порядка, у которого собственная
частота равна единице, т.е.
![]() .
.
Для ИУ второго порядка
 (П2.19)
(П2.19)
где
![]() - оптимальное значение относительного
коэффициента демпфирования, при котором
относительная ширина ППЧ максимальна.
Его можно вычислить по формуле
- оптимальное значение относительного
коэффициента демпфирования, при котором
относительная ширина ППЧ максимальна.
Его можно вычислить по формуле
 .
(П2.20)
.
(П2.20)
Соответствующее максимальное значение относительной ширины ППЧ равно
![]() .
(П2.21)
.
(П2.21)
На рис. П2.8 показан
типичный график зависимости
![]() от
от
![]() .
Видно, что этот график состоит из двух
ветвей (соответствующих формулам
(П2.19)) и имеет характерный разрыв в точке
.
Видно, что этот график состоит из двух
ветвей (соответствующих формулам
(П2.19)) и имеет характерный разрыв в точке
![]() ,
справа от которой
,
справа от которой
![]() .
Слева от этой точки
.
Слева от этой точки
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
.
На рис. П2.9 показан
график оптимальной АЧХ типового ИУ
второго порядка (кривая 1). В точке своего
максимума он касается границы
![]() . В результате относительная ширина
полосы ППЧ
. В результате относительная ширина
полосы ППЧ
![]() принимает максимально возможное (для
заданных
принимает максимально возможное (для
заданных
![]() и
и
![]() )
значение
)
значение
![]() .
Если
.
Если
![]() ,
то экстремум АЧХ выходит за верхнюю
границу трубки точности (см. кривую 2 на
рис. П2.9), т.к. в этом случае
,
то экстремум АЧХ выходит за верхнюю
границу трубки точности (см. кривую 2 на
рис. П2.9), т.к. в этом случае![]() и, напротив, если
и, напротив, если
![]() ,
то
,
то
![]() (см. кривую 3 на рис. П2.9).
(см. кривую 3 на рис. П2.9).



Рис. П2.8. Рис. П2.9.
В обоих случаях точка первого выхода АЧХ за границы трубки точности смещается влево, т.е. ширина ППЧ уменьшается
П2.2.5. Интегральные показатели качества переходного процесса
Квадратичная интегральная оценка для типового ИУ второго порядка вычисляется по формуле
![]() .
(П2.22)
.
(П2.22)
Исследование этой
функции двух переменных на наличие
экстремума (минимума) в области
устойчивости
![]() , позволяет сделать следующие выводы:
, позволяет сделать следующие выводы:
-
ИКОП обратно пропорциональна собственной частоте ИУ
 ,
т.е. чем больше
,
т.е. чем больше
 ,
тем меньше ИКОП;
,
тем меньше ИКОП; -
при любом заданном значении собственной частоты ИУ
 существует оптимальное значение
относительного коэффициента демпфирования
существует оптимальное значение
относительного коэффициента демпфирования
 ,
при котором ИКОП минимальна (в этом
случае
,
при котором ИКОП минимальна (в этом
случае
 ).
).
На рис. П2.10 показаны
графики соответствующих переходных
процессов для трех значений собственной
частоты ИУ:
![]() (сплошная кривая) и
(сплошная кривая) и
![]() (пунктирная кривая) и
(пунктирная кривая) и
![]() (штрих-пунктирная кривая).
(штрих-пунктирная кривая).


![]()
![]()
![]()





Рис. П2.10.
Видно, что при
увеличении
![]() происходит сжимание (а при уменьшении
происходит сжимание (а при уменьшении
![]() - растягивание) этих графиков вдоль оси
абсцисс при
сохранении их формы. Стремление
приблизить фактический переходный
процесс к идеальному ступенчатому
переходному процессу (за счет снижения
ИКОП) приводит к нежелательному
перерегулированию
- растягивание) этих графиков вдоль оси
абсцисс при
сохранении их формы. Стремление
приблизить фактический переходный
процесс к идеальному ступенчатому
переходному процессу (за счет снижения
ИКОП) приводит к нежелательному
перерегулированию
![]() и колебательности оптимального
переходного процесса. В этом проявляется
главный недостаток ИКОП.
и колебательности оптимального
переходного процесса. В этом проявляется
главный недостаток ИКОП.
![]()
Обобщенная квадратичная оценка для квазистатического ИУ второго порядка вычисляется по формуле
![]() .
(П2.23)
.
(П2.23)
Исследование этой
функции на наличие минимума в области
![]() и
и
![]() позволяет сделать следующие выводы:
позволяет сделать следующие выводы:
-
для каждого значения
 существуют такие значения
существуют такие значения
 и
и
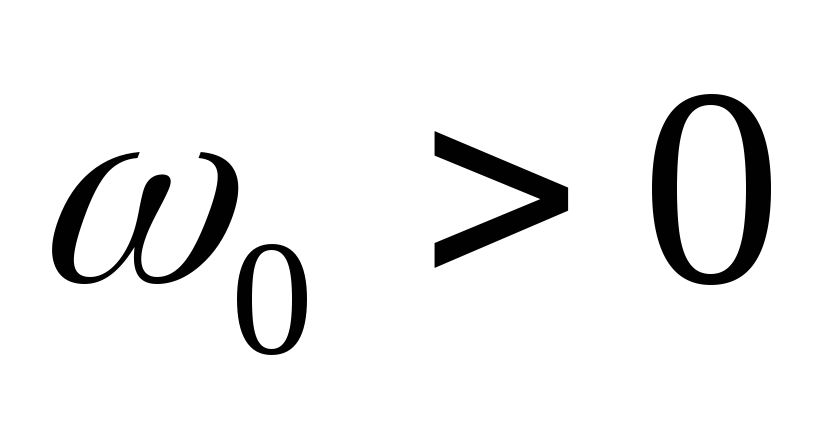 ,
при которых значение ОБИКОП (П2.23)
оказывается минимальным. Соответствующие
значения
,
при которых значение ОБИКОП (П2.23)
оказывается минимальным. Соответствующие
значения
 ,
,
 и
и
 должны быть связаны друг с другом
соотношением
должны быть связаны друг с другом
соотношением
![]() ;
(П2.24)
;
(П2.24)
-
чем больше собственная частота ИУ
 ,
тем больше относительный коэффициент
демпфирования
,
тем больше относительный коэффициент
демпфирования
 , меньше значение ОБИКОП и тем ближе
расположены друг к другу графики
фактического и экстремального переходных
процессов ИУ.
, меньше значение ОБИКОП и тем ближе
расположены друг к другу графики
фактического и экстремального переходных
процессов ИУ.
На рис. П2.11 эти
графики показаны для случая
![]() с
и ряда значений
с
и ряда значений
![]() и
и
![]() , вычисленных в соответствии с формулой
(П2.24). Видно, что с ростом собственной
частоты ИУ
, вычисленных в соответствии с формулой
(П2.24). Видно, что с ростом собственной
частоты ИУ
![]() графики фактических переходных процессов
приближаются к графику экстремального
переходного процесса.
графики фактических переходных процессов
приближаются к графику экстремального
переходного процесса.


Рис. П2.11.
П2.3. Динамические характеристики ИУ третьего порядка
П2.3.1. Передаточная функция
Типовое ИУ третьего порядка обычно образуется в результате последовательного соединения инерционного и колебательного звеньев, - например, инерционного датчика первичной информации и стрелочного отсчетного устройства (рис. П2.12). В этом случае передаточная функция ИУ имеет вид
![]() ,
где
,
где![]() .
(П2.25)
.
(П2.25)
Примером такого ИУ является терморезисторный термометр, рассмотренный в разделе 3.3.

Рис. П2.12.
В общем случае передаточная функция квазистатического ИУ третьего порядка имеет вид
 ,
(П2.26)
,
(П2.26)
где
![]() -
коэффициент чувствительности ИУ;
-
коэффициент чувствительности ИУ;
![]() - собственная частота;
- собственная частота;
![]() - параметры Вышнеградского;
- параметры Вышнеградского;
![]() - постоянная времени ИУ.
- постоянная времени ИУ.
Переход от одной
формы записи передаточной функции ИУ
(П2.25) к другой форме (П2.26) осуществляется
с помощью формул, связывающих параметры
![]() с параметрами
с параметрами
![]() и наоборот. Если известны параметры
и наоборот. Если известны параметры
![]() и
и
![]() ,
то соответствующие значения параметров
,
то соответствующие значения параметров
![]() и
и
![]() можно вычислить по формулам
можно вычислить по формулам
![]() ,
,
![]() ,
,
![]() ,
(П2.27)
,
(П2.27)
Наоборот, если
известны
![]() и
и
![]() ,
то
,
то
![]() и
и
![]() вычисляются по формулам
вычисляются по формулам
![]() ,
,
![]() ,
,
![]() ,
(П2.28)
,
(П2.28)
где
![]() ,
,
![]() -
положительный вещественный корень
кубического уравнения
-
положительный вещественный корень
кубического уравнения
![]() .
(П2.29)
.
(П2.29)
Например, если
![]() и
и
![]() ,
то
,
то
![]() и
и
![]() .
.
Представление
передаточной функции типового ИУ
третьего порядка в форме (П2.25) возможно
во всех случаях. Однако указанные выше
звенья такого ИУ могут оказаться
виртуальными, т.е. не имеющими конкретного
физического исполнения в приборе. В
этих случаях схему на рис. П2.12 нужно
рассматривать как эквивалентную
структурную схему типового ИУ третьего
порядка. В любом случае операторная
часть его передаточной функции
![]() содержит три коэффициента:
содержит три коэффициента:
![]() (или
(или
![]() ),
которые только и влияют на показатели
динамической точности ИУ.
),
которые только и влияют на показатели
динамической точности ИУ.
П2.3.2. Переходная функция. Диаграмма Вышнеградского
Переходную функцию
типового ИУ третьего порядка можно
получить как реакцию второго звена
структурной схемы ИУ, показанной на
рис. П2.12, на выходной сигнал первого
звена
![]() ,
соответствующий единичному входному
сигналу
,
соответствующий единичному входному
сигналу![]() .
В результате получим:
.
В результате получим:
-
если
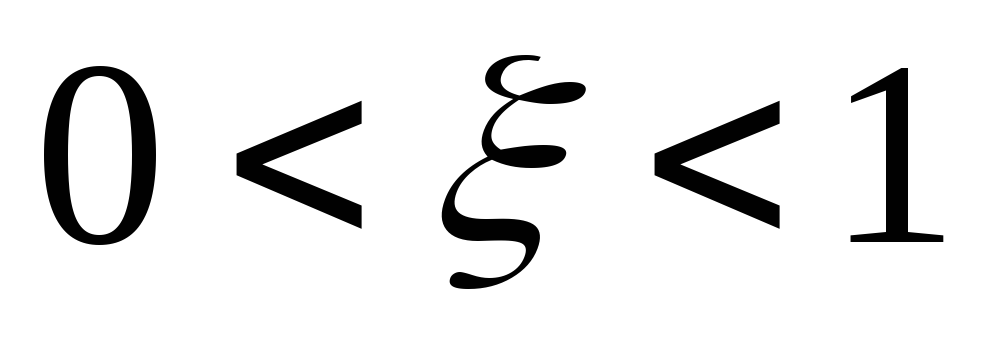 ,
то
,
то
![]() ,
(П2.30)
,
(П2.30)
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() - безразмерное время.
- безразмерное время.
-
если
 ,
то
,
то
![]() .
(П2.31)
.
(П2.31)
-
если
 ,
то
,
то
![]() (П2.32)
(П2.32)
где
![]() ,
,
![]() ,
,
![]() .
.
Отсюда следует,
что форма переходной характеристики
типового ИУ третьего порядка зависит
только от параметров
![]() и
и
![]() ,
или, учитывая формулы (П2.27), - только от
параметров Вышнеградского
,
или, учитывая формулы (П2.27), - только от
параметров Вышнеградского
![]() .
.
На рис. П2.13, а показана диаграмма Вышнеградского. С ее помощью удобно исследовать влияние корней характеристического уравнения типового ИУ третьего порядка на форму переходной характеристики такого ИУ.
На рис. П2.13, б
показан вид этой диаграммы в плоскости
параметров
![]() .
На обеих диаграммах выделены три области
1,2,3, соответствующие разным сочетаниям
корней характеристического уравнения
ИУ
.
На обеих диаграммах выделены три области
1,2,3, соответствующие разным сочетаниям
корней характеристического уравнения
ИУ
![]() .
(П2.33)
.
(П2.33)


а б
Рис. П2.13.
Уравнения границ этих областей приведены в таблице П2.3. Им соответствуют разные формы переходного процесса (рис. П2.14).


а б в г
Рис. П2.14.
В областях 1 и 2
уравнение (П2.33) имеет один отрицательный
вещественный корень
![]() и два комплексно-сопряженных корня
и два комплексно-сопряженных корня
![]() (
(![]() ).
В области 1 выполняется условие
).
В области 1 выполняется условие
![]() .
В этом случае апериодическая составляющая
переходного процесса
.
В этом случае апериодическая составляющая
переходного процесса
![]() затухает быстрее, чем колебательная
составляющая
затухает быстрее, чем колебательная
составляющая
![]() .
Поэтому для этой области характерен
колебательный переходный процесс,
подобный показанному на рис. П2.14, а.
.
Поэтому для этой области характерен
колебательный переходный процесс,
подобный показанному на рис. П2.14, а.
В области 2, напротив,
![]() ,
что соответствует монотонно-периодическому
переходному процессу (см. рис. П2.14, б)
. В области 3 все корни действительные,
отрицательные и разные. Поэтому переходный
процесс, соответствующий этой области,
является монотонным (см. рис. П2.14, в).
,
что соответствует монотонно-периодическому
переходному процессу (см. рис. П2.14, б)
. В области 3 все корни действительные,
отрицательные и разные. Поэтому переходный
процесс, соответствующий этой области,
является монотонным (см. рис. П2.14, в).
Кривая
![]() (на рис. П2.13, б
– прямая
(на рис. П2.13, б
– прямая
![]() ),
называемая гиперболой
Вышнеградского,
является границей устойчивости ИУ.
Пунктирная кривая
),
называемая гиперболой
Вышнеградского,
является границей устойчивости ИУ.
Пунктирная кривая
![]() соответствует таким значениям параметров
ИУ, при которых его переходная
характеристика два раза последовательно
касается границ трубки точности
соответствует таким значениям параметров
ИУ, при которых его переходная
характеристика два раза последовательно
касается границ трубки точности
![]() (см. рис.П2.14, г).
В этом случае относительная длительность
переходного процесса минимальна, т.е.
(см. рис.П2.14, г).
В этом случае относительная длительность
переходного процесса минимальна, т.е.
![]() . Каждой точке на этой кривой соответствует
определенное значение максимальной
относительной переходной погрешности
. Каждой точке на этой кривой соответствует
определенное значение максимальной
относительной переходной погрешности
![]() ,
причем по мере приближения к точке
,
причем по мере приближения к точке
![]() оно уменьшается, а значение
оно уменьшается, а значение
![]() возрастает.
возрастает.
Таблица П2.3.




 ,
,