239

Приложение 1.

Преобразование Лапласа и его свойства

Преобразованием по Лапласу функции вещественной переменной x = x(t) называется функция X=X(p) комплексной переменной , вычисляемая по формуле

. (П1.1)

Зная функцию , можно найти функцию по формуле

, (П1.2)

где - мнимая единица; - число превышающее показатель роста функции .

Функция , полученная в результате вычисления интеграла (П1.1), называется изображением, а функция x(t), подвергаемая преобразованию Лапласа, - оригиналом.

Прямое и обратное преобразования Лапласа символически записывают как и соответственно.

В таблице П1.1 даны изображения функций, которые наиболее часто встречаются в практике инженерных расчетов.

Изображения различных комбинаций этих функций, их производных, интегралов и пр. можно определить, зная свойства преобразования Лапласа. Эти свойства сформулируем в виде десяти теорем:

1. Теорема линейности: , где ; (П1.3)

2. Теорема подобия: , где a > 0; (П1.4)

3. Теорема запаздывания: 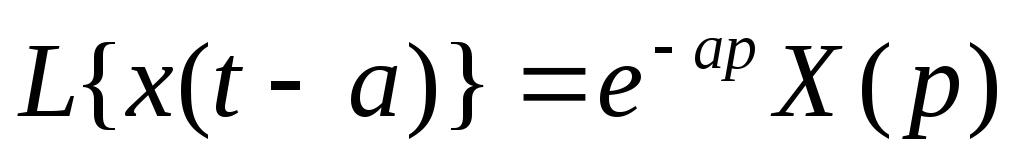, где a > 0; (П1.5)

4. Теорема смещения: , (П1.6)

где - любое (в т.ч. комплексное) число;

5. Терема о дифференцировании оригинала:

, (П1.7)

где - значение функции справа от нуля;

Таблица П1.1.

Преобразования Лапласа простых функций.

№	Оригинал	Название функции	График функции	Изображение
1		Функция Дирака, функция
2		Единичная, ступенчатая
3	,	Степенная
4	,	Показательная
5		Гармонический синус
6		Гармонический косинус
7	,	Затухающий синус
8	,	Затухающий косинус

Распространяя эту формулу на производные более высоких порядков, можно получить изображение ой производной функции

(П1.8)

6. Теорема о дифференцировании изображения:

; (П1.9)

7. Теорема об интегрировании оригинала: ; (П1.10)

8. Теорема об интегрировании изображения: ; (П1.11)

8. Теорема о предельных значениях: если существуют пределы и , то их можно вычислить по формулам

, . (П1.12)

10. Теорема умножения:

, (П1.13)

где символ означает свертку функций x(t) и y(t), т.е. свертку оригиналов сомножителей;

Если изображение X(p) представляет собой правильную дробно - рациональную функцию (правильную дробь), т.е. если

, где m < n , (П1.14)

то его оригиналом является следующая функция

. (П1.15)

Здесь - корни уравнения ; - кратность корня ; N - число различных корней уравнения .

Оригинал такого изображения можно найти также с помощью разложения правильной рациональной дроби на сумму простых дробей.

Если все корни уравнения простые, то формула разложения (П1.15) принимает следующий (более простой) вид

, (П1.16)

где - производные полинома при (т.е. ) .

При использовании этой формулы исчезает необходимость разложения сложной дроби на сумму простых дробей, что часто облегчает расчеты. Покажем пример такого расчета.

Пример П1.1: Определить оригинал изображения .

Решение: В этом случае , , , , т.е. , а уравнение имеет два простых корня , . Поэтому

.

С целью проверки правильности расчета определим изображение найденного оригинала

,

что совпадает с исходными данными.

Приведенные формулы справедливы для случаев, когда дробь (П1.14) правильная, т.е. выполняется условие . Если , то в результате деления полиномов числителя и знаменателя дроби образуется остаток в виде полинома ой степени. В этом случае разложение дроби можно записать в виде

, (П1.17)

где - полином степени ; - постоянные коэффициенты.

Соответствующий оригинал имеет вид

. (П1.18)

Здесь - оригинал правильной дроби (его можно найти обычным путем так, как это было показано выше); - функция го порядка . Покажем пример такого расчета.

Пример П1.2: Определить оригинал изображения .

Решение: Преобразуя заданную дробь, можно записать

.

Переходя в этом выражении к оригиналам, получим

.

Пример П1.3: В качестве еще одного примера покажем определение преобразования Лапласа для функции времени

,

которая отсутствует в Таблице П1.1.

П р и м е ч а н и е: весьма распространенной ошибкой при решении подобной задачи является поиск изображений сомножителей и их последующее перемножение.

Решение: В соответствии с теоремой о дифференцировании изображения (теоремой 6) можно записать .

После вычисления производной получим

.

При решении этой задачи можно было воспользоваться теоремой смещения (теоремой 4), согласно которой , где . В свою очередь, в соответствии с теоремой о дифференцировании изображения, можно записать

.

Осуществляя в этой формуле замену , получим прежний результат.

Изображения по Лапласу различных функций несложно вычислять в среде MATHCAD [26].

Приложение 2.