7.4. Характеристики случайных измерительных сигналов

Свойства случайных сигналов оценивают с помощью статистических (вероятностных) характеристик. Они представляют собой неслучайные функции и (или) числа, зная которые, можно судить о закономерностях, которые присущи случайным сигналам, но проявляются только при их многократных наблюдениях.

а б

в

Рис. 7.6.

7.4.1. Характеристики случайных сигналов, не изменяющихся во времени

Основными статистическими характеристиками сигнала, представленного случайной величиной (7.2), являются: функция распределения , плотность распределения вероятностей(ПРВ), математическое ожидание, дисперсия, среднеквадратическое отклонение (СКО)и доверительный интервал. Рассмотрим эти характеристики.

1. Функция распределения (или интегральный закон распределения) выражает вероятность того, что конкретное значение случайной величиныокажется меньше, чем ее заданное значение, т.е.

, (7.64)

где - символ вероятности события.

2. Плотность распределения вероятностей (или дифференциальный закон распределения) представляет собой функцию текущего значения случайной величины , выражающую вероятность попадания конкретного значения случайной величины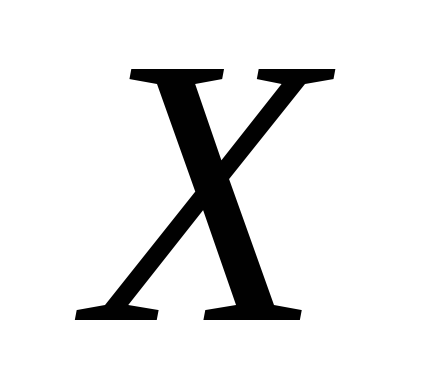в малый интервал ее возможных значений, примыкающий к, т.е.

. (7.65)

Размерность ПРВ обратна размерности величины.

2. Математическое ожидание определяет средневзвешенное значение случайной величины и вычисляется по формуле

, (7.66)

Результат вычислений по этой формуле отличается от среднего значения случайной величины и совпадает с ним только в случае симметричных законов распределения (равномерного, нормального и других).

Величина называется центрированной случайной величиной. Математическое ожидание такой величины равно нулю.

4. Дисперсия случайной величины определяет средневзвешенное значение квадрата отклонения этой величины от ее математического ожидания. Дисперсия вычисляется по формуле

(7.67)

и имеет размерность, совпадающую с размерностью квадрата величины

5. Среднеквадратическое отклонение вычисляется по формуле

(7.68)

и, в отличие от дисперсии , имеет размерность, совпадающую с размерностью измеряемой физической величины. Поэтому СКО оказывается более удобным показателем степени разброса возможных значений случайной величины относительно ее математического ожидания.

В соответствии с правилом «трех сигм», практически все значения случайной величины, обладающей нормальным законом распределения, попадают внутрь интервала , примыкающего к математическому ожиданию этой величины.

6. Доверительным интервалом называется диапазон возможных значений случайной величины, в котором эта величина находится с заранее заданнойдоверительной вероятностью . Этот диапазон можно записать в виде, или в виде

, (7.69)

т.е. границы доверительного интервала расположены симметрично относительно математического ожидания сигнала , а площадь криволинейной трапеции с основаниемравна доверительной вероятности(рис. 7.7). С ростомдоверительный интервалтакже увеличивается.

Половину доверительного интервала можно определить, решая уравнение

. (7.70)

В практике инженерных расчетов наиболее широкое применение среди перечисленных статистических характеристик случайного сигнала получила ПРВ . Зная ПРВ, можно определить все другие статистические характеристики сигнала. Поэтому функцияявляетсяполной статистической характеристикой случайного сигнала.

Рис. 7.7.

Укажем на основные свойства ПРВ:

1. , т.е. ПРВ - неотрицательная функция;

2. и , т.е., зная ПРВ , можно определить функцию распределения случайной величиныи, наоборот, зная функцию распределения, можно определить ПРВ;

2. Площадь криволинейной трапеции под графиком ПРВ с основанием равна вероятности события, т.е.

, (7.71)

Отсюда следует условие нормировки ПРВ

. (7.72)

так как вероятность события равна единице. Если все возможные значения измеряемой случайной величины занимают интервал, то условие нормировки ПРВ имеет вид

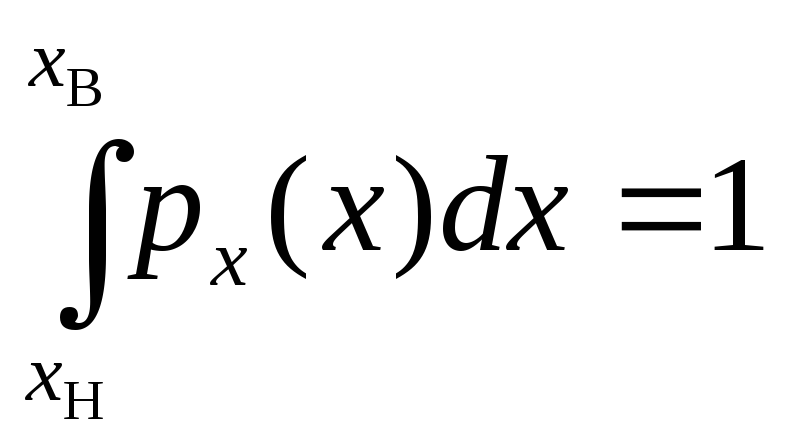, (7.73)

В любом случае, площадь криволинейной трапеции, образованной графиком ПРВ, равна единице. Это условие можно использовать для определения аналитического вида (формулы) ПРВ , если известны только форма графика или только вид этой функции (см. Приложение 5, задача 7.6) [28].

7.4.2. Характеристики системы случайных сигналов

Процесс измерения характеризуется наличием множества случайных величин и событий, участвующих в формировании результата измерения. Помимо самой измеряемой величины, сюда входят неинформативные параметры объекта контроля, параметры средства измерений, параметры окружающей среды и даже состояние потребителя измерительной информации. Их совокупное влияние на результат измерения выражается в том, что этот результат, полученный вновь при (казалось бы) неизменных условиях измерений, отличается от прежнего результата. Проводя повторные измерения и накапливая данные (статистику), можно, во - первых, составить представление о степени разброса результатов измерений и, во - вторых, попытаться выяснить влияние каждого фактора на погрешность результата измерений.

Если рассматриваются несколько (две и более) случайных величин , то они образуютсистему случайных величин. Такая система кроме перечисленных выше характеристик для каждой случайной величины в отдельности имеет дополнительные характеристики, позволяющие оценить уровень статистических связей между всеми случайными величинами, образующими систему. Такими характеристиками являются корреляционные моменты (ковариации) для каждой пары случайных величин, . Они вычисляются по формуле

, (7.74)

где -двумерная ПРВ системы двух случайных величин и(с математическими ожиданиямиисоответственно), характеризующаясовместное распределение этих величин.

При отсутствии статистической связи между величинами исоответствующий корреляционный момент равен нулю (т.е.). Такие случайные величины называютсястатистически независимыми.

При выполнении математических операций со случайными величинами, имеющими известные статистические характеристики, важно уметь определять статистические характеристики результатов этих операций. Ниже такие характеристики приводятся для простейших математических операций:

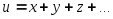1. Математическое ожидание и дисперсияалгебраической суммы нескольких случайных величин равны

(7.75)

Если величины статистически независимые, то . т.е. дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин.

В таблице 7.2. приведены формулы для определения характеристик суммы двух случайных величин. В этом случае ,, а дисперсияи СКОрезультата суммирования существенно зависят от величины относительного коэффициента корреляции суммируемых величин, где.

Таблица 7.2.

Статистические характеристики суммы двух случайных величин

Относительный коэффициент корреляции	Дисперсия	СКО
0
1
-1

Равенство соответствует случаю, когда изменение величинывсегда влечет за собой изменение величиныи всегда в ту же сторону, что и, т.е.. Если знаки изменений этих величин всегда противоположны друг другу, то. Наконец, если величиныиимеют конечные дисперсии и статистически не зависят друг от друга, то. Обратное утверждение справедливо только для нормально распределенных случайных величин [2].

2. Математическое ожидание и дисперсиялинейной функции нескольких случайных величин , где- постоянные коэффициенты, равны

, (7.76)

;

Если величины статистически независимые, то

(7.77)

3. Математическое ожидание и дисперсияпроизведениядвух независимых случайных величин равны

, . (7.78)

4. Математическое ожидание 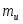и дисперсияпроизведениятрех независимых случайных величин равны

, .

5. Математическое ожидание и дисперсияслучайной величины, являющейся известнойфункцией непрерывной случайной величины , ПРВкоторой также известна , равны

,

. (7.79)

Аналогично, если - известная функция двух непрерывных случайных величин , совместная (двумерная) ПРВ которыхизвестна, то математическое ожиданиеи дисперсиютакой случайной величины можно определить по формулам

, (7.80)

.

Все предыдущие формулы для вычисления результатов математических операций со случайными величинами можно получить из этих общих формул.

7.4.3. Типовые распределения случайных сигналов

Рассмотрим статистические характеристики непрерывных случайных величин, имеющих типовые распределения.

7.4.3.1. Равномерное распределение.

В случае равномерного распределения случайная величина (7.2) с одинаковой плотностью вероятности попадает в каждую точку ограниченного интервала . ПРВи функция распределениятакой случайной величины имеют вид (рис. 7.8)

(7.81)

Рис. 7.8.

Другие (частные) статистические характеристики такой случайной величины можно вычислить по формулам

, ,,. (7.82)

7.4.3.2. Треугольное распределение (распределение Симпсона)

В этом случае график ПРВ имеет форму треугольника с вершиной в точке , а график интегрального закона распределения представляет собой плавное сопряжение двух парабол в точке, где,,(рис. 7.9).

(7.83)

Рис. 7.9.

Математическое ожидание и дисперсию такой случайной величины можно вычислить по формулам

, . (7.84)

Если , то распределение Симпсона становитсясимметричным. В этом случае

, ,,. (7.85)

7.4.3.3. Нормальное распределение (распределение Гаусса)

Нормальное распределение относится к одному из наиболее часто встречающихся распределений случайных величин. Отчасти это связано с тем, что распределение суммы большого числа независимых случайных величин, обладающих различными законами распределений, часто встречающееся на практике, приближается к нормальному распределению. В этом случае ПРВ и функция распределения имеют вид

, . (7.86)

СКО и математическое ожидание такой величины совпадают с параметрами распределения, т.е.,.

Доверительный интервал не выражается через элементарные функции, но всегда может быть найден из уравнения (7.70). Результат решения этого уравнения для заданного значения доверительной вероятностиможно записать в виде, где- квантиль, значение которого зависит от уровня доверительной вероятности.

Существуют табличные значения функции [10]. Приведем некоторые из них:

, ,,,........

Отсюда видно, что с довольно высокой вероятностью () практически все значения случайной величины, обладающей нормальным распределением, попадают в интервал, имеющий ширину. Это свойство положено в основу правила «трех сигм».

На рис. 7.10 показаны графики ПРВ и интегрального закона нормального распределения для двух различных значений СКО ( ) и одинакового математического ожидания.

Рис. 7.10.

Видно, что график ПРВ представляет собой одногорбую «резонансную» кривую с максимумом в точке , расположенную симметрично относительно математического ожидания. Эта кривая тем «острее», чем меньше СКО. Соответственно, тем меньше разброс возможных значений случайной величины относительно ее математического ожидания. Однако во всех случаях площадь криволинейной трапеции, ограниченной графиком ПРВ, равна единице (см. (7.72)).

В теории вероятностей кроме рассмотренных выше характеристик применяют еще и другие характеристики случайной величины: характеристическую функцию, эксцесс, контрэксцесс, квантильные оценки и пр. Однако, рассмотренных характеристик вполне достаточно для решения большинства практических задач измерительной техники. Покажем пример решения такой задачи.

Пример 7.4.: Требуется определить параметр А (координату вершины) плотности распределения вероятностей случайного измерительного сигнала, график которой показан на рис. 7.11 (предполагается, что известна только форма этого графика).

Требуется также определить вероятность того, что величина (модуль) сигнала будет больше, чем его СКО , т.е. требуется определить вероятность события.

Рис. 7.11.

Решение: Значение параметра А определим из условия нормировки ПРВ (7.73), которое в данном случае имеет вид

.

Здесь первое слагаемое соответствует площади прямоугольника, лежащего на рис. 7.11 под графиком ПРВ левее пунктирной линии , второе - площади прямоугольного треугольника, лежащегоправее этой линии. Из полученного уравнения находим . С учетом этого результата, плотность распределения вероятностей можно записать в виде

Теперь можно вычислить математическое ожидание , дисперсиюи СКОсигнала. По формулам (7.66), (7.67) и (7.68) соответственно получаем:На рис. 7.11 штрихпунктирными линиями показаны границы интервала.

В соответствии с условием нормировки (7.71), искомая вероятность равна сумме площадей под графиком ПРВ, расположенных левее точки (в данном примере эта площадь равна нулю) и правее точки, т.е.

.

7.4.4. Характеристики случайных сигналов, изменяющихся во времени

Случайный сигнал, изменяющийся во времени в общем случае содержит детерминированную (систематическую) и центрированную случайную (флуктуационную) составляющие, т.е.

. (7.87)

На рис. 7.12 показан график одной из ряда возможных реализаций такого сигнала. Пунктиром показана его детерминированная составляющая , вблизи которой группируются и вокруг которой колеблются все другие реализации сигнала.

Рис. 7.12.

Полное представление о характеристиках такого сигнала дает генеральная (полная) совокупность всех его реализаций. На практике она всегда конечна. Поэтому характеристики случайного сигнала, найденные опытным путем, следует считать оценками его действительных характеристик.

В каждый момент времени (т.е. в каждом сечении сигнала) значения случайной функции времени (7.87) представляют собой случайную величинус соответствующими статистическими характеристиками, рассмотренными выше. В частности, детерминированная составляющая случайного сигнала в каждый момент времени совпадает сматематическим ожиданием соответствующей случайной величины , т.е.

, (7.88)

где - одномерная ПРВ случайного процесса (7.87), которая, в отличие от рассмотренной выше ПРВ случайной величины (7.65), зависит не только от, но еще и от времени.

Степень разброса реализаций случайного сигнала относительно его систематической составляющей (7.88) характеризует максимальное значение модуля флуктуационной составляющей сигнала и оценивается по величине СКО этой составляющей , которое в общем случае также зависит от времени

. (7.89)

где - дисперсия случайного сигнала, вычисляемая по формуле

. (7.90)

Для каждого момента времени можно определить доверительный интервал (см. (7.70)), а затем построитьдоверительную область, т.е. такую область, в которую реализации случайного сигнала попадают с заранее заданной доверительной вероятностью(рис. 7.13).

Рис. 7.13.

Трех рассмотренных характеристик (и) достаточно для того, чтобы составить общее представление о свойствах случайного измерительного сигнала (7.87). Однако, их недостаточно, чтобы судить о внутреннем составе (спектре) такого сигнала.

На рис. 7.14, в частности, показаны графики реализаций двух различных случайных сигналов с одинаковыми математическим ожиданием и СКО. Отличие этих сигналов выражается в различном спектральном (частотном) составе их реализаций, т.е. в разной степени статистической связи между значениями случайного сигнала в два момента времени и, отстоящих друг от друга на величину. Для сигнала, показанного на рис. 7.16,а эта связь более сильная, чем для сигнала на рис. 7.14, б.

а б

Рис. 7.14.

В теории случайных процессов подобная статистическая связь оценивается с помощью автокорреляционной функции случайного сигнала (АКФ), которая вычисляется по формуле

, (7.91)

где -двумерная ПРВ сигнала.

Различают стационарные и нестационарные случайные сигналы. Если сигнал (7.87) стационарный, то его математическое ожидание (7.88) и дисперсия (7.90) не зависят от времени, а его АКФ (7.91) зависит не от двух аргументов и, а только от одного аргумента - величины временного промежутка. Для такого сигнала

, ,, где. (7.92)

Другими словами, стационарный случайный сигнал является однородным по времени, т.е. его статистические характеристики не изменяются при изменении точки отсчета времени.

Если, помимо стационарности, случайный сигнал является еще и эргодическим, то , а его автокорреляционную функцию можно вычислить по формуле

, (7.93)

не требующей знания двумерной ПРВ так как в этой формуле в качествеможно использоватьлюбую реализацию сигнала. Дисперсию такого (стационарного и эргодического) сигнала можно вычислить по формуле

, (7.94)

Достаточным условием эргодичности случайного сигнала является стремление к нулю его АКФ при неограниченном росте временного сдвига[2].

АКФ случайного сигнала часто нормируется к дисперсии. В этом случае безразмерная нормированная АКФ вычисляется по формуле

. (7.95)

На рис. 7.15 показан типичный график такой АКФ.

Рис. 7.15.

Зная эту функцию, можно определить интервал корреляции , т.е. время, по истечении которого значения случайного сигнала можно считатьстатистически не зависящими друг от друга

. (7.96)

Из этой формулы следует, что площадь под графиком нормированной АКФ совпадает с площадью прямоугольника единичной высоты, имеющего в основании удвоенный интервал корреляции (см. рис. 7.15).

Поясним физический смысл интервала корреляции [2]. Если известна информация о поведении центрированного случайного сигнала «в прошлом», то возможен его вероятностный прогноз на время порядка интервала корреляции . Однако, прогноз случайного сигнала на время, превышающее интервал корреляции, окажется недостоверным, так как мгновенные значения сигнала, столь «далеко» отстоящие друг от друга во времени, являются практически некоррелированными (т.е. статистически не зависящими друг от друга).

В рамках спектрально - корреляционной теории случайных процессов для описания свойств стационарного случайного сигнала достаточно знать только его АКФ , или толькоэнергетический спектр сигнала . Эти две функции связаны друг с другом формулами Винера – Хинчина [2,15]

, (7.97)

, (7.98)

т.е. каждой функции частоты соответствует вполне определенная функция временного сдвигаи наоборот, каждой АКФ соответствует вполне определенная спектральная плотность мощности стационарного случайного сигнала. Поэтому, зная энергетический спектр флуктуационной составляющейслучайного сигнала (7.87), можно определить АКФ этой составляющейи наоборот. Это подтверждает то, что частотные и корреляционные характеристики стационарного случайного сигнала тесно связаны друг с другом.

Свойства АКФ случайного сигнала аналогичны свойствам АКФ детерминированного сигнала.

Автокорреляционная функция характеризуетстатистическую связь между значениями стационарного случайного сигнала в моменты времени, отстоящие друг от друга по оси времени на величину . Чем меньше эта связь, тем меньше соответствующее значение АКФ. Энергетический спектрхарактеризует распределение по оси частот энергий гармонических составляющих случайного сигнала.

Зная энергетический спектр , или АКФфлуктуационной составляющей сигнала (7.1), можно вычислить её дисперсиюи эффективную ширину спектра (полосу частот)по формулам

, (7.99)

, (7.100)

где - ордината точки максимума на графике функции.

Эффективная ширина спектра случайного спектра случайного сигнала аналогична активной ширине спектрадетерминированного сигнала, то есть, как и последняя, определяет такой диапазон частот, в пределах которого сосредоточена подавляющая часть средней мощности сигнала (см.(7.55)). Поэтому по аналогии с (7.55) ее можно определять из соотношения

. (7.101)

где - постоянный коэффициент, определяющий долю мощности случайного сигнала, приходящуюся на полосу частот(например, = 0,95).

На рис. 7.16 дана графическая иллюстрация формул (7.100) и (7.101). В первом случае полоса частот совпадает с основанием прямоугольника, имеющего высотуи площадь(рис. 7.19,а), во втором – с основанием криволинейной трапеции, имеющей площадь (рис. 7.16,б). Полоса частот узкополосного случайного процесса располагается в области , где- средняя частота спектра (рис. 7.16,в), и вычисляется из соотношения

.

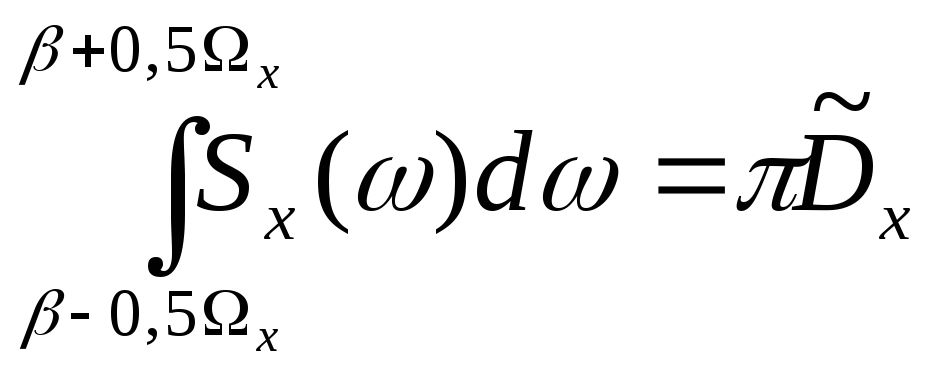Эффективную ширину спектра случайного сигнала можно определить множеством других способов [2, 15]. В любом случае величины идолжны быть связаны соотношением, подобным соотношению, имеющему место для детерминированных сигналов (см. раздел 7.3.3).

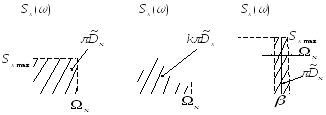
а б в

Рис. 7.16.

В таблице 7.3 приведены спектрально-корреляционные характеристики для трех стационарных случайных сигналов.

В первом пункте этой таблицы приведены характеристики так называемого белого шума - специфического случайного сигнала, значения которого, расположенные сколь угодно близко друг к другу, - независимые случайные величины. АКФ белого шума имеет форму  - функции, а его энергетический спектр содержит гармонические составляющие любых (в том числе сколь угодно высоких) частот. Дисперсия белого шума - бесконечно большое число, т.е. мгновенные значения такого сигнала могут быть сколь угодно большими, а его интервал корреляции равен нулю.

Таблица 7.3.

Характеристики стационарных случайных сигналов

№	Автокорреляционная функция	Интервал корреляции	Энергетический спектр
1
2
3

Во втором пункте таблицы указаны характеристики низкочастотного шума, а в третьем пункте – узкополосного шума. Если , то эти характеристики этих шумов близки друг к другу.

Случайный сигнал называется узкополосным, если частота значительно меньше средней частоты спектра. Узкополосный случайный сигнал можно записать в виде (см. (7.12)), где функциииизменяются значительно медленнее, чем функция.

Свойства спектрально - корреляционных характеристик стационарного случайного сигнала аналогичны свойствам амплитудного спектра и АКФ детерминированного сигнала. В частности, и- четные функции,и т. д. Есть и отличия. Отличие корреляционных функций заключается в том, что АКФ детерминированного сигналахарактеризует связь сигналаи его копии, а АКФ случайного сигнала- связь значений сигналаив разные моменты времени.

Различие между функциями изаключается в том, что функцияпредставляет собой не точный частотный образ случайного сигнала, а усредненную характеристику частотных свойств целого ансамбля различающихся между собой реализаций этого сигнала. Этот факт, а также отсутствие в энергетическом спектреинформации о фазах гармонических составляющих случайного сигнала не позволяет восстанавливать по нему форму этого сигнала.

Из формул (7.97) и (7.98) следует, что функции исвязаны друг с другом преобразованиями Фурье, т.е. (см. (7.46))

и .

Поэтому, чем шире спектр случайного сигнала (чем больше ), тем уже его АКФ и меньше интервал корреляции.