7.3. Характеристики детерминированных сигналов

7.3.1. Энергетические характеристики

К энергетическим характеристикам сигнала относятся мгновенная мощность сигнала , определяемая как квадрат его мгновенного значения

(7.15)

и производные от нее величины: энергия на интервале

(7.16)

и средняя мощность сигнала на интервале

. (7.17)

Примечание: Если - ток, то значение функциив каждый момент времени совпадает со значением мгновенной мощности, выделяемой при протекании этого тока через сопротивление в1 Ом. В общем случае в формуле (7.15) предполагается наличие единичного размерного множителя, переводящего размерность квадрата сигнала в размерность мощности.

Если и сигналзадан на полуоси, то в формулах (7.16) и (7.17) следует использовать предельный переход. В этом случае энергетическими характеристиками сигнала являются:

- полная энергия (далее просто энергия ) сигнала

; (7.18)

- средняя мощность (далее просто мощность ) сигнала

. (7.19)

Для периодических сигналов ( у которых )

, (7.20)

где - период сигнала; - любое число (значение интеграла (7.20) от этого числа не зависит).

7.3.2. Спектральные характеристики

7.3.2.1. Спектральные характеристики периодических сигналов

С помощью спектральных характеристик оценивают внутренний состав (спектр) сигнала. Для этого сигнал представляют в форме обобщенного ряда Фурье, раскладывая его по системе базисных функций

, (7.21)

где - постоянные коэффициенты, отражающие вклад функциив формирование значений сигнала на рассматриваемом промежутке времени.

Возможность представления сложного сигнала в виде суммы простых сигналовоказывается особенно важной длялинейных динамических систем. В таких системах выполняется принцип суперпозиции, т.е. их реакция на сумму воздействий (сигналов) равна сумме реакций на каждое из воздействий в отдельности (см. (8.2)). Поэтому, зная реакцию линейной системы на простой сигнал, можно, суммируя результаты, определить её реакцию на любой другой сложный сигнал.

Выбор функций подчиняют требованиям максимальной точности приближения сигналарядом (7.21) при минимальном числе членов этого ряда и, по возможности , снижению вычислительных трудностей, возникающих при определении коэффициентов ряда.

В качестве базисных функций наиболее широкое применение получили вещественные тригонометрические функции

(7.22)

и комплексные экспоненциальные функции

. (7.23)

На них строится классический спектральный анализ сигналов. Вместе с тем, возможно применение других систем базисных функций (функций Тейлора, Уолша, Лагерра, Эрмита, Лежандра, Чебышева, Котельникова и др. [2]), что в ряде случаев позволяет, учитывая специфику приближаемой функции , сократить число членов ряда (7.21) при сохранении заданной погрешности приближения.

В последние годы появилась новая весьма перспективная система базисных функций, называемых вейвлетами . В отличие от гармонических функций, они способны, изменяя свою форму и свойства, адаптироваться к локальным особенностям приближаемого сигнала. В результате становится возможным простое представление сложных сигналов (в том числе с локальными скачками и разрывами) наборами вейвлетов того или иного типа [2].

При использовании тригонометрических базисных функций (7.22), ряд (7.21) приобретает форму классического тригонометрического ряда Фурье

, (7.24)

где - частота основной гармоники ряда (Т - период сигнала); - целое число;- действительные числа (коэффициенты Фурье), вычисляемые по формулам

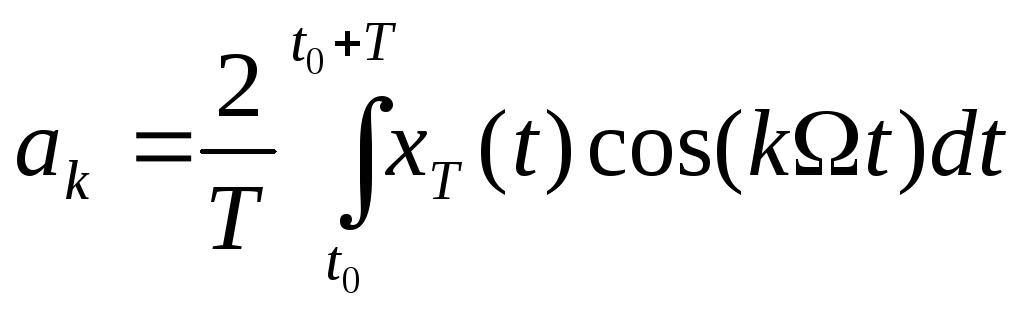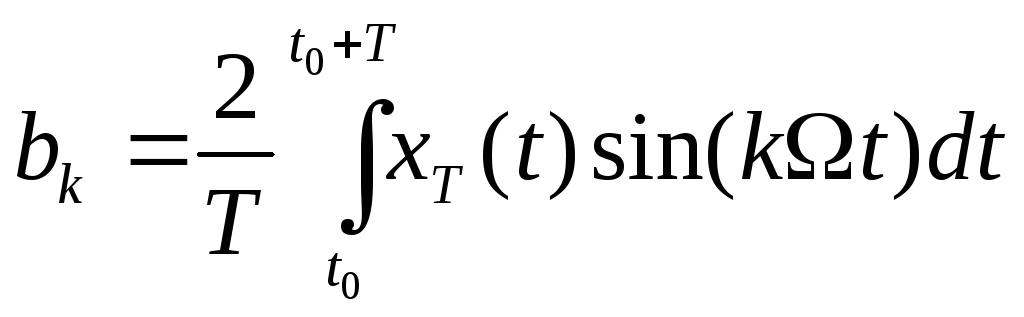, где ,

, где . (7.25)

В этих формулах, как и прежде (см. (7.20)), - произвольное число, которое можно выбирать из соображений удобства вычисления интегралов (7.25), так как значения этих интегралов от величиныне зависят; - базовый импульс сигнала (см. рис. 7.3, в).

Коэффициент определяет удвоенное среднее (за период) значение сигнала, остальные коэффициенты() - вклад- ой гармоники ряда Фурье (7.24) в формирование мгновенных значений сигнала.

Тригонометрический ряд Фурье (7.24) можно записать в двух других формах: в форме разложения по синусам

, (7.26)

и в форме разложения по косинусам

, (7.27)

где - постоянная составляющая сигнала;- амплитуда -ой гармоники ряда, вычисляемая по формуле

. (7.28)

Начальные фазы этих гармоник вычисляются из соотношений

, или . (7.29)

Совокупность амплитуд гармонических составляющих периодического сигнала называетсяамплитудным спектром этого сигнала. Совокупность начальных фаз этих составляющих -фазовым спектром сигнала.

Используя - функцию Дирака, оба спектра можно представитьрешетчатыми функциями частоты

, , (7.30)

т.е. амплитудный и фазовый спектры периодического сигнала являются дискретными спектрами. Это отличает периодический сигнал от всех других сигналов, обладающих сплошными спектрами.

Таким образом, периодический сигнал можно представить в виде суммы гармоник (7.24). При этом частота каждой гармонической составляющей ряда Фурье кратна частоте основной гармоники , зависящей от периода сигнала.

Чем больше таких гармоник, тем меньше погрешность приближения функции конечной суммой ряда Фурье (7.24). Исключением являются точки разрыва непрерывности функции. В окрестности таких точек проявляется так называемоеявление Гиббса [2]. Согласно этому явлению, в окрестности точек разрыва конечные суммы ряда Фурье

(7.31)

образуют осциллирующие «хвосты», высота которых не уменьшается с ростом числа учитываемых гармоник ряда Фурье – она составляет примерно 9% от величины скачка функциив точке разрыва.

Для вычисления амплитуды и начальной фазы k - ой гармоники периодического сигнала можно вместо формул (7.28) и (7.29) использовать другие формулы

, , (7.32)

где - изображение по Лапласу базового импульса сигнала, определяемое по формуле (см. Приложение 2)

; (7.33)

i - мнимая единица; - положительное целое число. Использование этих формул исключает необходимость вычисления интегралов (7.25), что значительно упрощает расчеты. Покажем пример такого расчета.

Пример 7.1. Определить амплитудный спектр периодического сигнала

. (7.34)

Решение: На рис. 7.3, а, показан график такого сигнала. Видно, что этот сигнал имеет период . Следовательно, частота основной гармоники соответствующего ряда Фурье (7.24) равна . Принимая,(для), по формулам (7.25) вычислим коэффициенты Фурье

, где ,, где.

Следовательно ,,где, т.е. разложение функциив тригонометрический ряд Фурье имеет вид

. (7.35)

Примечание: здесь принято (а не) из-за использования знака «минус» перед суммой гармоник ряда.

Рис. 7.3.

На рис. 7.3, б показан амплитудный спектр рассматриваемого сигнала. Значение амплитуды k - ой гармоники ряда представлено вертикальным отрезком соответствующей длины, в основании которого указан номер гармоники.

Следует иметь в виду, что амплитуды некоторых гармоник ряда Фурье могут быть равны нулю. Кроме того, не обязательным является монотонное уменьшение амплитуд этих гармоник с ростом номера гармоники, как это имеет место на рис. 7.3,б. Однако, во всех случаях должно выполняться условие , вытекающее из требования сходимости ряда Фурье.

Решим задачу с использованием формул (7.32). Для этого сначала найдем изображение по Лапласу базового импульса сигнала

.

Подставляя сюда ( гдеi - мнимая единица, ), получим

, ,

что совпадает с прежними результатами.

В технических приложениях часто пользуются комплексной формой записи ряда Фурье

. (7.36)

В этом случае в качестве базисных функций используются комплексные экспоненциальные функции (7.23). Поэтому коэффициенты ряда (7.36) становятсякомплексными. Они вычисляются по формуле

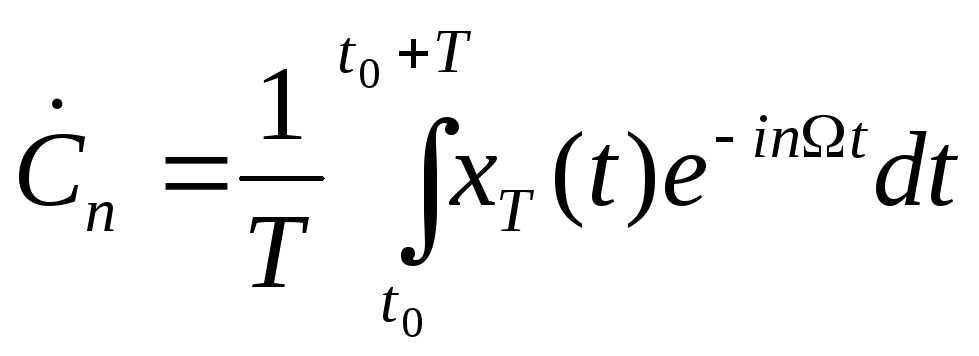, (7.37)

где, как и в формуле (7.6), индексная переменная может быть как положительным, так и отрицательным целым числом.

При использовании комплексной формы ряда Фурье (7.36) спектром амплитуд периодического сигнала называют множество абсолютных величин комплексных коэффициентов Фурье

, где n = 0,  1,  2,... (7.38)

а спектром фаз - множество главных аргументов этих коэффициентов

. (7.39)

Множество величин называетсяспектром мощности периодического сигнала, а множество комплексных чисел - спектральной последовательностью периодического сигнала. Именно эти три характеристики (спектр амплитуд, спектр фаз и спектр мощности) относят к основным спектральным характеристикам периодического сигнала.

В отличие от амплитудного и фазового спектров периодического сигнала, представленного в форме тригонометрического ряда Фурье (7.24), спектры того же сигнала, построенные с использованием комплексных коэффициентов Фурье (7.37), оказываются двухсторонними . Это является следствием наличия в (7.36) «отрицательных частот» (для отрицательных значений n). Последние, разумеется, не существуют в реальности . Они только отражают используемое при формировании комплексного ряда Фурье представление экспоненциальной гармонической функции в виде единичного вектора, вращающегосяпо часовой стрелке с угловой скоростью .

Если существует изображение по Лапласу базового импульса периодического сигнала , то спектр амплитуд и спектр фаз периодического сигнала можно вычислять по формулам

, , где. (7.40)

Известны и успешно применяются на практике алгоритмы так называемого быстрого преобразования Фурье, благодаря которым удается настолько снизить время вычисления коэффициентов Фурье, что спектры сигналов при их обработке получают практически в режиме реального времени [2].

В заключение отметим три наиболее важных свойства спектральных характеристик периодического сигнала:

1. Если - четная функция, то мнимые составляющие всех комплексных коэффициентов Фурьеравны нулю и, напротив, если эта функция нечетная, то вещественные составляющие всех комплексных коэффициентов Фурьеравны нулю.

2. В точке разрыва первого рода функциисумма ряда Фурьеравна полусумме предельных значений функции при приближении аргумента к точке разрываслева и справа, то есть

.

П р и м е ч а н и е: если значения функции на концахбазового импульсане равны друг к другу, то при периодическом продолжении импульса эти точки становятся точками разрыва первого рода.

3. Мощности периодического сигнала во временной и частотной областях равны друг другу, то есть

. (7.41)

Это соотношение выражает теорему Парсеваля.

Наличие в формуле (7.36) «отрицательных частот» (для) иногда отмечают как недостаток комплексной формы ряда Фурье. Однако, именно эта форма позволяет естественным образом распространить результаты спектрального анализа периодических детерминированных сигналов на сигналы, описываемые непериодическими функциями времени, чему посвящен следующий раздел.

7.3.2.2. Спектральные характеристики непериодических сигналов

Выделим из непериодического сигнала (на рис. 7.4 показан сплошной кривой) «базовый импульс», имеющий длительностьТ, и введем в рассмотрение периодическую функцию времени

. (7.42)

На рис. 7.4 график этой функции показан пунктиром.

Рис. 7.4.

Представим эту функцию в форме комплексного ряда Фурье (7.36)

. (7.43)

Выполняя в (7.43) предельный переход, можно получить интегральное представление исходного (непериодического) сигнала

, (7.44)

где комплексная функция частоты , называемаяспектральной плотностью сигнала, связана с вещественной функцией времени соотношением

. (7.45)

П р и м е ч а н и е: При выполнении предельного перехода () в формуле (7.43) происходят следующие трансформации обозначений:

, ,,.

Соотношения (7.45) и (7.44) называются, соответственно, прямым и обратным преобразованиями Фурье сигнала . Пользуются следующей условной формой записи этих преобразований

, . (7.46)

Прямое преобразование Фурье (7.45) «переводит» вещественную функцию времени в комплексную функцию частоты, сохраняя при этом взаимно однозначное соответствие этих функций, или, как иногда говорят, «переводит сигнал из временной плоскости в частотную плоскость». В результате появляется возможность оперировать не с формой сигнала, а с его частотным образом.

Такое (частотное) представление сигнала часто оказывается более компактным. Кроме того, упрощаются некоторые сложные математические операции с вещественным сигналом . Например, дифференцирование «переводится» в умножение. Упрощается также расчет реакциилинейного инерционного ИУ на детерминированный сигналзаданной формы (см. раздел 8.2.2).

Спектральную плотность сигнала как комплексную функцию частотыможно представить в виде

,

где - соответственно вещественная и мнимая части спектральной плотности сигнала, которые можно вычислить по формулам

,

.

- соответственно амплитудная частотная и фазовая частотная функции детерминированного сигнала, называемые его амплитудным и фазовым спектрами. Эти функции частоты вычисляются по формулам

, (7.47)

, (7.48)

а их графики называются соответственно амплитудно - частотной и фазо - частотной характеристиками сигнала.

Таким образом, измерительный сигнал также как и измерительное устройство имеет свои частотные характеристики: амплитудно-частотную и фазо-частотную.

В отличие от периодического сигнала (7.24) с дискретным спектром, непериодический сигнал (7.44) содержит непрерывный спектр колебаний с частотами , изменяющимися от 0 до. Амплитудный и фазовый спектры такого сигнала также являются непрерывными (сплошными), при этом амплитудный спектрописываетплотность распределения по оси частот амплитуд гармонических составляющих детерминированного сигнала, имеющих частоту , а фазовый спектр- фаз этих составляющих.

П р и м е ч а н и е: при практическом вычислении значений функции по формуле (7.48) нужно учитывать следующие свойства главного значения аргументакомплексного числа

(7.49)

Зная спектральную плотность сигнала , можно по формуле (7.44) полностью восстановить форму этого сигналаи, наоборот, зная функцию времени, можно по формуле (7.45) вычислить спектральную плотность сигнала. Поэтому комплексная функция частотыявляетсяполной спектральной характеристикой детерминированного сигнала.

Учитывая свойство при, спектральные характеристики непериодического детерминированного сигнала можно вычислять по формулам

, ,, (7.50)

где - изображение по Лапласу функции(см. Приложение 1). Использование этих формул часто существенно упрощает расчет спектральных характеристик детерминированного сигнала. Покажем пример такого расчета.

Пример 7.2: Определить амплитудный и фазовый спектры сигнала в виде прямоугольного единичного импульса длительности .

Решение: С помощью единичной ступенчатой функции времени , такой сигнал можно записать в виде (рис. 7.5,а)

. (7.51)

Преобразованием Лапласа такой функции служит . Подставляя сюда, находим

.

Следовательно, амплитудная частотная функция рассматриваемого сигнала выражается формулой

. (7.52)

При эта функция имеет неопределенность типа. Раскрывая ее по правилу Лопиталя, можно получить.

При построении фазового спектра сигнала необходимо учитывать изменение знака функциии правила (7.49). Так, например, еслии, тои. Если же, тои.

На рис. 7.5, б,в показаны графики амплитудного и фазового спектров сигнала (7.51) для случая с.

а б в

Рис. 7.5

В заключение перечислим основные свойства спектральных характеристик детерминированного сигнала:

1. Если прии , то Фурье - изображение функции совпадает с изображением этой функции по Лапласу, т.е., где.

Например, из соотношения следует соотношениеи т.д.

Сюда же можно отнести все свойства преобразования Лапласа, которые сформулированы в Приложении 1 в виде теорем линейности (П1.3), подобия (П1.4), запаздывания (П1.5) и др. Например, по аналогии с теоремой запаздывания, можно записать

, где .

Это означает, что если сигнал сдвигается по времени (т.е., если вместо функции рассматривается функция, где), то амплитудный спектр и спектр мощности этого сигнала не изменяются.

2. Амплитудная частотная функция вещественного сигналапредставляет собойположительную четную функцию частоты , а фазовая частотная функция-нечетную функцию частоты.

3. Если - периодический сигнал, базовый импульс которого есть, то график амплитудного спектра базового импульсас точностью до постоянного множителясовпадает с графиком огибающей спектра амплитуд периодического сигнала, т.е. эти графики подобны друг другу (см. рис. 7.5,б и рис. 8.1).

3. Зная амплитудный спектр детерминированного сигнала , можно определить спектр его мощности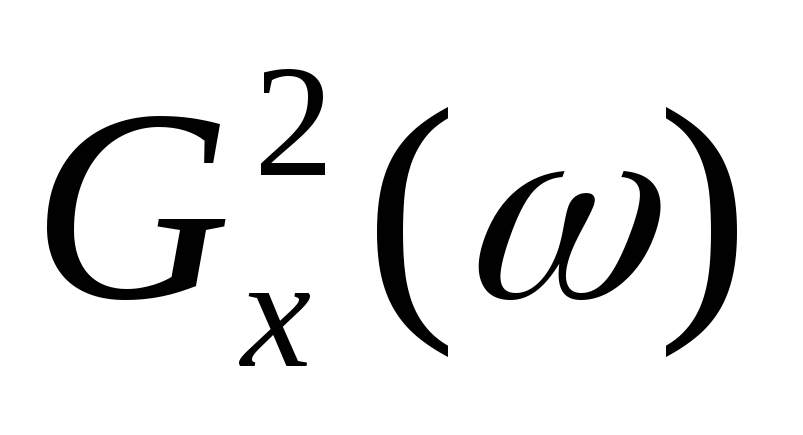, а затем - энергию сигналапо формуле

. (7.53)

Эта формула указывает на связь между спектральными и энергетическими характеристиками детерминированного сигнала.

Перечисленные свойства можно использовать для контроля правильности расчета спектральных характеристик сигналов.

7.3.3. Ширина спектра и активная длительность сигнала

Активную длительность и ширину спектрадетерминированного сигналаопределяют как интервал времении, соответственно, интервал частот, внутри которых сосредоточенаподавляющая часть энергии этого сигнала. В соответствии с данным определением, их значения можно определить из уравнений

, (7.54)

, (7.55)

где - коэффициент, определяющий упомянутую выше долю энергии сигнала (обычно принимают ).

Аналогично определяют ширину спектра случайного сигнала (см. (7.101)).

В случае простых одиночных импульсов (прямоугольного, треугольного, синусоидального и др.), спектры которых сосредоточены в области низких частот, выполняется приближенное равенство [3]. Из этого равенства следует, что уменьшение длительности сигнала приводит к увеличению ширины его спектра, и наоборот, чем шире спектр сигнала, тем меньше его длительность.

Полоса пропускания частот ИУ должна превышать ширину спектра измерительного сигнала, т.е. параметры ИУ должны быть такими, чтобы выполнялось условие

, или , (7.56)

где - ширина спектра детерминированной составляющей измерительного сигнала;- ширина спектра случайной составляющей сигнала;- символ, означающий выбор максимального числа из двух чисели.

В противном случае заметно проявляются динамические искажения сигнала, обусловленные инерционностью элементов ИУ.

Ширину спектра сигнала называют также полосой частот сигнала.

7.3.4. Корреляционные характеристики

С помощью корреляционных характеристик оценивают наличие связей отдельных частей сигнала друг с другом или связь одного сигнала с другим сигналом. В первом случае используется автокорреляционная функция сигнала (АКФ) , во втором -взаимная корреляционная функция сигналов (ВКФ) .

Автокорреляционная функция детерминированного сигнала , заданного на интервалеи ограниченного по энергии (7.19), т.е. сигнала, у которого, выражается в единицах энергии и вычисляется по формуле

. (7.57)

При имеем. В этом случае связь сигнала с самим собой наибольшая. Соответствующее максимальное значение АКФ равно энергии сигналат.е.

. (7.58)

С увеличением аргумента (величины сдвига) функцияу всех сигналов,кроме периодических, убывает (не обязательно монотонно) и при относительном сдвиге сигналов ина величину, превышающую активную длительность сигнала, практически обращается в нуль.

АКФ детерминированных сигналов, обладающих бесконечно большой энергией и ограниченных по мощности (7.19), т.е. таких сигналов, у которых , выражается в единицах мощности и вычисляется подругой формуле

. (7.59)

Для таких сигналов .

При определении АКФ периодического сигнала усреднение можно выполнять по периоду , т.е. для периодического сигнала

. (7.60)

где - базовый импульс сигнала.

Контроль за правильностью расчета АКФ детерминированного сигнала можно осуществлять по признаку выполнения следующих свойств этой функции:

1. , т.е. АКФ - четная функция.

2. , т.е. абсолютные значения АКФ не могут превышать ее значения при .

3. АКФ следующим образом связана со спектром мощности сигнала

,

и наоборот

, (7.61)

т.е. АКФ и спектр мощности детерминированного сигнала связаны друг с другом преобразованиями Фурье. Отсюда следует, что расчет АКФ детерминированного сигнала можно выполнять по следующей схеме

.

Покажем пример такого расчета

Пример 7.3.: Определить АКФ сигнала .

Решение: Для такого сигнала имеем

, ,

и следовательно ,. Распространяя полученный результат на область, окончательно можно записать.

4. Если , то, т.е. АКФ периодического сигнала есть также периодическая функция с тем же периодом. Это свойство можно использовать для выделения периодической составляющей измерительного сигнала из смеси сигнала с помехой.

5. Если , где, то.

6. Если , где, то.

Взаимная корреляционная функция детерминированных сигналов и, ограниченных по энергии, вычисляется по формуле

, (7.62)

и в общем случае не является четной функцией. Она достигает максимума при таком значении аргумента , при котором сигналыимаксимально похожи друг на друга.

Если хотя бы один из сравниваемых сигналов обладает бесконечной энергией, то вместо (7.62) следует, по аналогии с (7.59), записать ВКФ в единицах мощности

. (7.63)

На рис. 7.6, б показана ВКФ двух импульсов: прямоугольного и треугольного, сдвинутых друг относительно друга на 1с (рис. 7.6, а). Видно, что максимум ВКФ достигается при с. При такой величине временного сдвига (аргумента ВКФ) импульсы максимально связаны друг с другом (рис. 7.6,в) .