6.3. Синтез иу по критериям динамической точности

6.3.1. Синтез параметров передаточной функции ИУ

Параметрическим синтезом передаточной функции ИУ называется определение таких значений ее параметров, при которых ИУ имеет заданные (желаемые) динамические характеристики. В общем случае такими параметрами являются коэффициенты операторной части передаточной функции ИУ (5.81), зависящие от физических параметров схемы и конструкции ИУ. Эквивалентными параметрами являются нули и полюсы передаточной функции ИУ.

Рассмотрим решение этой задачи для квазистатических ИУ первого, второго и третьего порядков с передаточными функциями вида

, (6.31)

, (6.32)

(6.33)

где - коэффициенты дифференциального уравнения ИУ (5.2);- коэффициент чувствительности ИУ,- постоянная времени ИУ,- собственная частота ИУ,- относительный коэффициент демпфирования,- параметры Вышнеградского.

ИУ с такими передаточными функциями часто встречаются в измерительной технике. Поэтому рассматриваемая задача имеет большое практическое значение.

В Приложении 2 даны формулы, с помощью которых можно вычислить все динамические характеристики таких ИУ (полные и частные). По аналогии с типовыми динамическими звеньями, устройства с такими передаточными функциями можно называть типовыми ИУ.

Число коэффициентов передаточной функции, влияющих на динамические характеристики таких ИУ, совпадает с порядком их характеристического уравнения . Для ИУ первого порядка таким коэффициентом является постоянная времени, для ИУ второго порядка – собственная частота(или постоянная времени) и относительный коэффициент демпфирования, для ИУ третьего порядка - собственная частота(или постоянная времени) и параметры Вышнеградского. Коэффициент чувствительностина показатели динамической точности ИУ не влияет.

Если известны физические параметры схемы и конструкции ИУ, то можно определить коэффициенты его дифференциального уравнения (5.2), а затем - параметры передаточной функции

, ,,,. (6.34)

После этого можно, используя формулы Приложения 2, вычислить показатели динамической точности ИУ, т.е. решить задачу анализа динамических характеристик ИУ. Решая задачу параметрического синтеза, необходимо, напротив, определить такие значения параметров ИУ, при которых выполняются заданные требования к его динамическим характеристикам. Эта задача решается в обратном порядке, т.е. сначала определяются параметры передаточной функции ИУ , а затем – параметры схемы и конструкции ИУ. Покажем порядок решения таких задач для типовых ИУ.

6.3.1.1. Параметрический синтез ИУ первого порядка

Единственным параметром относительной передаточной функции типового ИУ первого порядка (6.31) является постоянная времени . Если на длительность переходного процессав таком ИУ наложено требование, где- допустимое значение длительности переходного процесса, то выбор постоянной времени ИУнужно подчинить условию (см. табл. П2.1)

, (6.35)

где - допустимое значение относительной переходной погрешности.

Выбор конкретного значения может быть связан с интервалом времени, необходимым для получения результата измерения. Это особенно важно, когда ИУ используется в режиме «обслуживания очереди», например, при сортировке по размеру (или массе) деталей, последовательно поступающих на измерительную позицию.

Если ИУ используется для измерения меняющейся во времени величины, то к его динамическим характеристикам может предъявляться другое требование , где- минимально допустимое значение ширины полосы пропускания частот. В этом случае выбор постоянной времени ИУ следует подчинить другому условию (см. табл. П2.1)

, (6.36)

где - допустимое значение относительной частотной погрешности.

Выбор значения в формуле (6.36) может быть связан с необходимостью выполнения условия, где- полоса частот измерительного сигнала (см. (7.56)).

6.3.1.2. Параметрический синтез ИУ второго порядка

Относительная передаточная функция типового ИУ второго порядка (6.32) содержит два параметра, влияющих на динамические характеристики такого ИУ: собственную частоту (или постоянную времени) и относительный коэффициент демпфирования.

Из (6.32) следует, что, неограниченно увеличивая , можно (независимо от значения) получать сколь угодно малые динамические искажения измерительного сигнала, так как с ростом собственной частоты ИУ. На практике это требование может входить в противоречие с требованием получения необходимой чувствительности ИУ. Например, увеличение собственной частоты термометра, рассмотренного в разделе 3.2, приводит к уменьшению чувствительности подвижной системы прибора. Кроме того, требования к динамическим характеристикам не всегда предусматривают полное отсутствие инерционности ИУ. Например, из соображений фильтрации помех, бывает необходимо сократить ширину полосы пропускания частот ИУ, что требует снижения.

Расчет желаемых значений изависит от состава и характера тех требований, которые предъявляются к динамическим характеристикам ИУ. В таблице 6.1 приведены типовые сочетания таких требований и алгоритмы решения соответствующих (типовых) задач синтеза.

Таблица 6.1.

Алгоритмы синтеза параметров относительной передаточной функции

ИУ второго порядка

№	Показатели динамической точности					Алгоритм расчета параметров передаточной функции
1		-	-	-
2		-	-	-
3		-	-	-
4		-		-	-
5		-	-		-
6	-		-	-	-	[Щеп,1].

Пункт 1 этой таблицы соответствует случаю, когда от ИУ требуется минимальная длительность переходного процесса () и заданное значение ширины ППЧ (). В этом случае относительный коэффициент демпфированиявычисляется по формуле (П2.11), а форма переходной характеристики ИУ должна иметь вид кривой1, показанной на рис. П2.3 (Приложение 2). Соответствующее минимальное значение длительности переходного процесса вычисляется по формуле , где расчет величинывыполняется по приближенной формуле (П2.7) или так, как показано на рис. П2.3.

С помощью алгоритма п. 2 можно определить такие значения и, при которых ИУ имеет максимальную ширину ППЧ () и заданную длительность переходного процесса (). В этом случае относительный коэффициент демпфирования вычисляется по формуле (П2.20), а форма АЧХ должна быть такой, как показано на рис. П2.9 (кривая 1). Соответствующее максимальное значение ширины ППЧ вычисляется по формуле, где величинавычисляется по формуле (П2.21).

Пункт 3 соответствует случаю, когда нужно получить заданные значения и. Эта задача имеет решение, еслии. Поэтому при ее решении необходимо предварительно решить задачи п.1 и п.2.

В остальных пунктах таблицы 6.1 рассматривается случаи, когда требования предъявляются только к показателям качества переходного процесса. В п. 4 такими требованиями является получение заданных значений перерегулирования () и длительности переходного процесса (). В п. 5 и п. 6 рассматриваются случаи, когда для оценки переходного процесса используются интегральные показатели качества. В работе [28] даны примеры таких расчетов.

6.3.1.3. Параметрический синтез ИУ третьего порядка

Алгоритмы синтеза параметров передаточной функции типового ИУ третьего порядка (с передаточной функцией (6.33)) практически не отличаются от приведенных в таблице 6.1. Отличие заключается только в том, что вместо одного безразмерного параметра , влияющего на форму динамических характеристик ИУ, нужно определять два таких параметра: параметры Вышнеградского, или параметрыи(см. раздел П2.3. Приложения 2).

В качестве примера покажем расчет оптимальных параметров сильфонного пневматического прибора, предназначенного для автоматического контроля овальности деталей (рис. 6.14).

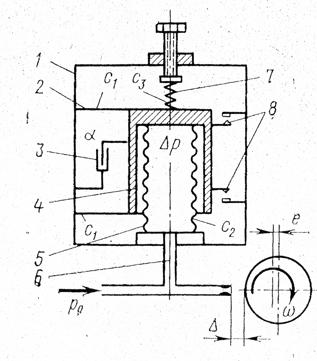
Рис. 6.14

Пример 6.5: В корпусе 1 прибора на двух плоских пружинах 2 жесткостью Н/м каждая подвешен цилиндр 4 массой, соединенный с сильфоном 5, имеющим осевую жесткостьН/м. Давление воздуха в сильфон подается через трубопровод 6, имеющий выход в зазор 9 между соплом пневматического преобразователя и контролируемой деталью 10. Усилие предварительного натяга и регулировка прибора осуществляются пружиной 7 жесткостью. Для успокоения нежелательных колебаний цилиндра в схему прибора введен демпфер вязкого трения 3. Создаваемая им сила демпфированияпропорциональна скорости перемещения цилиндра, т.е., где- постоянный коэффициент, зависящий от конструктивных параметров демпфера.

Изменение давления в сильфоне пропорционально изменению зазора 9, т.е . , где- давление, соответствующее номинальному зазору. Если деталь имеет эксцентриситети вращается с угловой скоростью, то зазор и давление воздуха в сильфоне изменяются по гармоническому закону, т.е.и. Если овальность сложная (полигармоническая), тои- периодические функции времени. При изменении давления возникает движущая сила(где- эффективная площадь сильфона), под действием которой цилиндр перемещается. Если овальность контролируемой детали выходит за пределы поля допуска, то происходит замыкание одного из контактов 8 и подается сигнал на отбраковку. Допустимая динамическая погрешность прибора 2%.

Необходимо определить жесткость пружины 7 и коэффициент демпфирования демпфера, при которых обеспечиваются максимальная ширина полосы пропускания частоти заданная длительность переходного процессас , возникающего при установке детали на измерительную позицию. В этом случае достигается максимальная скорость вращения контролируемой детали, что в свою очередь способствует максимальной производительности контрольно-сортировочного автомата. Рассматриваемые требования соответствуют пункту 2 таблицы 6.1.

Решение: Примем в качестве обобщенной координаты перемещение цилиндра 4 относительно положения равновесия. Тогда его движение описывается дифференциальным уравнением второго порядка

, (6.37)

где - суммарная жесткость подвеса;- движущая сила, амплитудакоторой пропорциональна овальности контролируемой детали. Соответствующая относительная передаточная функция прибора эквивалентна передаточной функции ИУ второго порядка (6.32)

, (6.38)

где - постоянная времени,- относительный коэффициент демпфирования (степень успокоения свободных колебаний) и собственная частота прибора, вычисляемые по формулам (6.34). Определим значения этих параметров, подчиняя их выбор выполнению заявленных требований.

Условие максимума ширины полосы пропускания частот выполняется, если относительный коэффициент демпфирования равен (см. (П2.20))

.

Соответствующие относительную длительность переходного процесса , относительную ширину полосы пропускания частот, верхнюю границу полосы пропускания частот, собственную частотуи постоянную времени прибораможно вычислить, используя методики расчета и формулы из раздела П2.2 Приложения 2. В результате получим

,,,,мс.

На рис. 6.15 пунктирными кривыми 1 показаны соответствующие АЧХ (рис. 6.15, а) и переходная характеристика прибора (рис. 6.15, б). Видно, что форма АЧХ является оптимальной (см. рис. П2.9, кривая 1), требование к длительности переходного процесса (с) также выполняется

Зная коэффициенты передаточной функции (6.38), можно определить искомые параметры прибора

H/м, Нс/м (6.39)

Если учесть инерционность воздушной магистрали, то вместо (6.38) получим

, (6.40)

где - постоянная времени воздухопровода;- постоянная времени подвижной системы прибора;- параметры Вышнеградского.

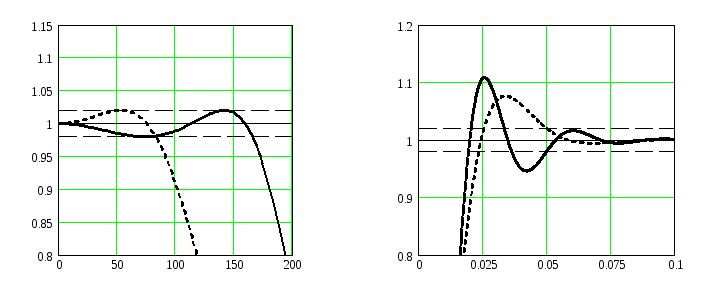
a б

Рис. 6.15.

Определим, какими должны быть параметры прибора в этом случае. Используя данные таблицы П3.2 для случая находим

, или (см. (П2.28)),.

В этом случае ,, т.е.

, .

Следовательно (см. (П2.28)), мс,мс.

В результате искомые жесткость регулировочной пружины 7 и коэффициент демпфирования демпфера равны (см. (6.39))

H/м, Нс/м. (6.41)

На рис. 6.15 сплошными кривыми 2 показаны соответствующие динамические характеристики прибора: АЧХ (рис. 6.15, а) и переходная характеристика (рис. 6.15, б). Видно, что все требования к показателям динамической точности выполняются.

6.3.2. Структурный синтез передаточной функции ИУ

Часто изменение параметров ИУ нежелательно или даже невозможно. В этих случаях выполнение требований может достигаться введением в схему прибора специального корректирующего звена. Выбор схемы и параметров этого звена подчиняют требованиям к динамическим характеристикам ИУ.

6.3.2.1. Аналоговая коррекция динамических характеристик типовых ИУ

Возможны различные схемы и способы включения аналоговых КЗ. Наиболее распространенным способом является последовательное включение (рис. 6.16).

В этом случае передаточная функция скорректированного ИУ равна произведению передаточных функций звеньев, т.е.

, (6.42)

где - передаточная функция корректируемого ИУ.

Рис. 6.16.

Передаточная функция КЗ подбирается так, чтобы передаточная функция скорректированного ИУ совпадала с желаемой передаточной функцией прибора. Для рассматриваемых типовых ИУ она принимается в виде

, ,, (6.43)

где и- желаемые значения параметров передаточной функции (при которых выполняются требования к динамическим характеристикам ИУ), т.е. имеет тот же вид, что и передаточная функция корректируемого ИУ (см. (6.31) - (6.33)), но другие (желаемые) значения параметров. В этом случае справедливо соотношение

, (6.44)

где вычисляется по формулам (6.43). В таблице 6.2 даны вид и параметры передаточных функций звеньев, необходимых для коррекции динамических характеристик типовых ИУ. Их можно строить с использованием операционных усилителей [28].

Таким образом, расчет передаточной функции КЗ сводится к расчету желаемых значений параметров передаточной функции прибора. Покажем пример такого расчета.

Таблица 6.2.

Передаточные функции корректирующих звеньев

№ п/п	Передаточная функция корректируемого ИУ	Передаточная функция корректирующего звена
		Вид	Параметры
1
2
3

Пример 6.6: Пусть требования к динамическим характеристикам ИУ сводятся к выполнению следующих условий

, c, , () , (6.45)

а структурная схема ИУ такая, как показано на рис. 6.17. Необходимо установить необходимость использования КЗ и (в случае такой необходимости) определить его передаточную функцию.

Решение: 1) Определим передаточную функцию ИУ . Для этого запишем уравнение, связывающее изображения по Лапласу входного и выходного сигналов

.

Отсюда найдем

, (6.46)

где - соответственно коэффициент чувствительности ИУ и операторная часть передаточной функции ИУ

, . (6.47)

Рис. 6.17.

2. Установим необходимость включения КЗ .

Рассматриваемое устройство является типовым квазистатическим ИУ второго порядка с параметрами (см. (6.32)) с,. На рис. 6.18 показаны переходная характеристика (рис.6.18,а) и относительная АЧХ (рис.6.18, б ) такого ИУ. Соответствующие значения показателей динамической точности ИУ можно определить по формулам раздела П2.2 Приложения 2. В результате получим

. (6.48)

Видно, что ни одно из требований (6.45) не выполняется. Поэтому коррекция динамических характеристик рассматриваемого ИУ необходима.

2. Определим передаточную функцию КЗ . Согласно формулам п. 2 таблицы 6.2, она имеет вид

, (6.49)

где с,,,. В этом случае вместо (6.46) получим

, (6.50)

где - желаемые значения параметров передаточной функции ИУ. Их выбор нужно подчинить выполнению заданных требований.

а б

в г

Рис. 6.18.

Требование обеспечивается если(см. раздел П2.2.3 Приложения 2 ). Полагаядля случаяс помощью формул раздела П2.2 Приложения 2 получим,. Теперь подберем такое значение собственной частоты ИУ, чтобы выполнялись требования к длительности переходного процесса и ширине полосы пропускания частот. Если выбрать, то получими, что не противоречит условиям (6.45). Поэтому в (6.50) можно принятьс,.

Передаточная функция соответствующего КЗ имеет вид (см. (6.49))

. (6.51)

Для создания звена с такой передаточной функцией можно использовать операционные усилители [28].

2. Проверим выполнение заданных требований.

На рис. 6.18, в,г показаны графики переходного процесса (рис.6.18, в) и АЧХ (6.18,г) скорректированного ИУ. Видно, что все требования, предъявляемые к показателям динамической точности ИУ, выполняются.

Эффективность КЗ можно оценить по величине относительного изменения корректируемого показателя динамической точности ИУ. Если цель коррекции состоит в снижении длительности переходного процесса, то показатель эффективности КЗ определяется в виде

, (6.52)

где - длительность переходного процесса в корректируемом ИУ;

- длительность переходного процесса в скорректированном ИУ.

Если в результате коррекции нужно расширить полосу пропускания частот ИУ, то

, (6.53)

где - ширина полосы пропускания частот корректируемого ИУ;

- ширина полосы пропускания частот скорректированного ИУ.

Если корректируется одновременно несколько показателей динамической точности, то показатель эффективности КЗ можно оценить по формуле

, (6.54)

где -ый частный показатель эффективности КЗ.

Чем выше , тем выше эффективность способа включения, вида и параметров передаточной функции корректирующего звена.

6.3.2.2 Цифровая коррекция динамических характеристик ИУ

В современных измерительных приборах и системах применяется цифровая алгоритмическая коррекция динамической погрешности результата измерений. В этом случае роль КЗ выполняет программируемое арифметико - логическое устройство (микроконтроллер), в котором осуществляются преобразования , исключающие динамическую погрешность.

Цифровое КЗ можно строить на основе цифрового фильтра, заменяющего аналоговое КЗ. Известны различные способы синтеза и расчета таких фильтров [7].

Контрольные вопросы

1. Поясните смысл терминов: анализ, синтез, оптимизация.

2. Поясните порядок решения проектной задачи.

3. Назовите методы параметрического синтеза статической характеристики прибора и дайте сравнительную характеристику этим методам.

4. Сформулируйте правило Новодворского.

5. Поясните постановку и порядок решения задачи параметрического синтеза методом интерполяции. Дайте пример решения такой задачи.

6. Поясните постановку и порядок решения задачи параметрического синтеза методом наименьших модулей. Дайте пример решения такой задачи.

7. Поясните постановку и порядок решения задачи параметрического синтеза методом наименьших квадратов. Дайте пример решения такой задачи .

8. Поясните постановку и порядок решения задачи структурного синтеза. Дайте пример решения такой задачи.

9. Поясните постановку и порядок решения задачи кусочно-линейной аппроксимации статической характеристики ИУ. Дайте пример решения такой задачи.

10. Поясните отличие сплайн-аппроксимации статической характеристики ИУ от кусочно-линейной аппроксимации этой характеристики.

11. Напишите передаточные функции типовых квазистатических ИУ первого, второго и третьего порядков. Укажите названия коэффициентов передаточных функций таких ИУ и поясните их влияние на динамические характеристики ИУ.

12. Поясните расчет постоянной времени и относительного коэффициента демпфированияИУ второго порядка с передаточной функциейисходя из требований, предъявляемых к показателям динамической точности такого ИУ. Приведите пример такого расчета.

13. Поясните расчет постоянной времени и параметров ВышнеградскогоИУ третьего порядка с передаточной функциейисходя из требований, предъявляемых к показателям динамической точности такого ИУ. Приведите пример такого расчета .

14. Поясните постановку и порядок решения задачи структурного синтеза ИУ по критериям динамической точности. Приведите пример расчета корректирующего звена.

271