Федеральное агенство по образованию

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МГУПИ

Шишков П.О.

Методические указания

по курсу

«ОСНОВЫ ОПТИКИ»

Часть 1

«ПОЛЯРИЗАЦИЯ»

Москвa 2006

Автор: Шишков П.О. - к.ф-м.н., доцент кафедры ПР-5 МГАПИ

Под общей редакцией д.т.н., проф. Слепцова В.В.

Рецензент: с.н.с. ИОФРАН Тихонов В.И.

Печатается по решению редакционно-издательского Совета МГУПИ

«___» ______________2005 г.

Председатель РИС Соколов В.В.

Учебное пособие рассмотрено и одобрено на заседании кафедры ПР-5

«___» ______________2005 г.

Зав.кафедрой ПР-5 Слепцов В.В.

Рекомендуется к печати методической комиссией факультета ПР

Протокол № от«___» _______________2005 г.

Председатель УМК

1. Основные понятия

Свет представляет собой электромагнитный волны, которые характеризуются одновременно двумя векторными физическими величинами: вектором напряженности электрического поля Е и вектором напряженности магнитного поли Н. Вектора Е и Н всегда перпендикулярны друг другу, расположены в плоскости, перпендикулярной направлению распространения волны, и составляют в любой момент времени и в любой точке пространства с направлением распространения правую тройку векторов. Таким образом электромагнитная волна представляет собой поперечную векторную волну. Пример мгновенного расположения векторов Е, Н и вектора скорости волны V показан на рис. 1.1.

Рис. 1.1.

Если волна движется вдоль оси Х , то вектора Е и Н всегда расположены в плоскости YOZ. По мере распространения волны вектора Е и Н могут менять как свою величину, так и направление в плоскости YOZ. Для идентификации изменения положения векторов Е и Н служит понятие поляризации.

Из теории электромагнитного поля известно, что как бы ни менялись величины и направления векторов Е и Н , в любой момент времени и в любой точке пространства соблюдаются два условия:

1. вектора Е и Н перпендикулярны друг другу,

1. абсолютные величины векторов Е и Н пропорциональны друг другу.

Для простоты рассмотрим случай плоской векторной синусоидальной электромагнитной волны.

Определение: плоская векторная волна называется синусоидальной, если проекции вектора физической величины на два

взаимноперпендикулярных направления, перпендикулярных направлению распространения, представляют собой плоские синусоидальные волны.

Если электромагнитная волна распространяется вдоль оси Х то применительно к вектору Е в соответствии с этим определением имеем

E=E_Y+E_Z.

E_Y=E₁cos(ωt-kx-α)

E_Z=E₂cos(ωt-kx-β) (1.1)

где E₁, E₂, ω, k, α, β - постоянные, t, x - переменные.

Пример мгновенного расположения проекций E_Y и E_Z приведен на рис. 1.2.

Рис. 1.2.

В выражении (1.1) величины имеют следующий смысл: E₁, E₂ - амплитуды проекций вектора Е на оси Y и X соответственно; ω - круговая частота; k=2π/λ - волновое число; α, β - начальные фазы; t - время; x – координата вдоль направления распространения.

Определим перемещение конца вектора Е при движении электромагнитной волны. Сначала зафиксируем какую-то плоскость пространства x=const и определим траекторию движения конца вектора Е в этой плоскости.

Обозначим:

φ₁=kx+α, φ₂=kx+β (1.2)

φ₁, φ₂ - фазы колебаний проекций E_Y и E_Z соответственно в плоскости x=const.

С учетом (1.2) выражения (1.1) перепишутся:

E_Y=E₁cos(ωt-φ₁)

E_Z=E₂cos(ωt-φ₂) (1.3)

Уравнения (1.3) можно рассматривать как уравнения траектории движения конца вектора Е в параметрическом виде, где параметром

служит время t.

Исключая t из уравнений (1.3), получим уравнение траектории конца вектора Е в данной плоскости x=const:

(1.4)

Это уравнение описывает кривую второго порядка, которая может быть только эллипсом, т.к. значения E_Y и E_Z изменяются лишь в ограниченных пределах: не выходят за пределы прямоугольника со сторонами 2E₁, 2E₂ как это видно из выражения (1.3) и рис. 1.3.

Рис. 1.3.

Знак обозначает, что волна движется перпендикулярно плоскости чертежа на нас.

Отсюда следует, что конец вектора Е описывает во всех точках пространства, вообще говоря, одинаковые и одинаково ориентированные эллипсы.

Таким образом, синусоидальная электромагнитная волна в общем случае эллиптически поляризована.

Примечание. Из свойств электромагнитной волны следует, что вектор Н также описывает эллипс в каждой точке пространства. Вращение по эллипсу векторов Е и Н в электромагнитной волне таково, что их мгновенное расположение представляет собой правую тройку векторов с направлением движения волны (см. рис. 1.4).

По мере распространения электромагнитной волны вектор Е будет вращаться по винтовой линии, расположенной на поверхности эллиптического цилиндра. Шаг винтовой линии равен длине волны излучения λ.

Рис. 1.4.

Рассмотрим частные случаи:

I) разность фаз колебаний проекций вектора Е равна четному числу π, т.е. проекции E_Y и E_Z колеблются в фазе (см. рис. 1.5):

φ₂-φ₁=2πm, m – любое целое число, x=const.

Рис. 1.5

Определим изменение положения вектора Е по истечении времени одного периода колебаний его проекций.

Последовательное положение вектора Е в плоскости YOZ в какой-то фиксированной точке пространства показано на рис.1.6 для различных моментов времени в течение одного периода колебаний Т от t=0 до t=T.

В момент времени t=0 проекции вектора E равны нулю и, следовательно, вектор Е=0.

Рис. 1.6.

В момент времени t=T/4, проекции E_Y и E_Z достигают максимальных значений, т.к. E_Y=E₁, E_Z=E₂ и E=E_Y+E_Z. В момент времени t=T/2 вектор Е опять становится равным нулю, Е=0. В момент времени t=3T/4 вектор Е опять достигает своего максимального значения, но уже расположен в III четверти, т.к. E_Y=-E₁, E_Z=-E₂. По истечении времени Т т.е. при t=T, вектор Е опять приходит в начало координат, т.к. E_Y=E_Z=0 и т.д.

Таким образом, вектор Е электромагнитной волны в каждой точке пространства совершает колебания по прямой линии, такая волна называется линейно или плоско поляризованной.

К такому же выводу можно прийти, подставив значения φ₂-φ₁=2πm в уравнение траектории (1.4). После подстановки получим следующие уравнения:

или (1.5)

Это уравнение прямой, расположенной в I и III четвертях координатной плоскости;

2) разность фаз колебаний проекций вектора Е равна нечетному числу π, т.е. проекции колеблются в противофазе:

φ₂-φ₁=(2m+1)π

m любое целое число.

Пример колебаний проекций при x=const приведен на рис. 1.7.

Рис. 1.7.

Рассматривая аналогично предыдущему случаю последовательность положений вектора Е в моменты времени t=0, T/4, T/2, 3T/4, T и т.д., получим, что вектор Е опять в каждой точке пространства совершает колебания по прямой линии, но уже во II и IV четвертях координатной плоскости (см. рис. 1.8).

Рис. 1.8.

Подставив φ₂-φ₁=(2m+1)π в уравнение траектории (1.4), получим уравнение прямой, изображенной на рис. 1.8:

или (1.6)

Таким образом, при φ₂-φ₁=(2m+1)π электромагнитная волна линейно или плоско поляризована;

3) разность фаз колебаний проекций вектора Е равна

φ₂-φ₁=±π/2+2πm (1.7)

Подставив это значение разности фаз в уравнение траекторий (1.4), получим:

Это каноническое уравнение эллипса.

В электромагнитной волне вектор Е в каждой точке пространства описывает эллипс, который своими главными осями ориентирован вдоль координатных осей. Электромагнитная волна - эллиптически поляризована.

Различают правую и левую эллиптические поляризации. Если φ₂-φ₁=+π/2+2πm, то в каждой точке пространства складываются колебания вида, приведенного на рис. 1.9.

Рис. 1.9

Сложив эти колебания в плоскости YOZ (см. рис. 1.10a), получим, что конец вектора Е описывает эллипс по часовой стрелке в этой фиксированной плоскости (если смотреть навстречу распространению волны). Такая волна имеет правую эллиптическую поляризацию. Это имеет полную аналогию с винтовой нарезкой винтов и гаек.

Рис. 1.10a.

Аналогичным образом можно показать, что при φ₂-φ₁=-π/2+2πm вектор Е описывает эллипс против часовой стрелки. Такая поляризация называется левой эллиптической поляризацией (см рис. 1.10б);

Рис. 1.10б.

4) разность фаз колебаний φ₂-φ₁=±π/2+2πm и проекции вектора Е равны по величине, т.е. E₁=E₂=E₀.

В этом случае уравнение (1.4) преобразуется в уравнение окружности:

(1.9)

т.е. конец вектора Е электромагнитной волны в каждой точке пространства описывает окружность. Такая волна называется поляризованной по кругу.

Если φ₂-φ₁=+π/2+2πm и E₁=E₂, то конец вектора Е описывает окружность по часовой стрелке - правая круговая поляризация (Рис. 1.11а).

Если φ₂-φ₁=-π/2+2πm и E₁=E₂, то конец вектора Е описывает окружность против часовой стрелки - левая круговая поляризация (Рис. 1.11б).

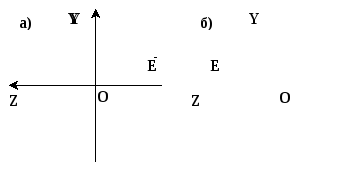
Рис. 1.11.

Таким образом, если в электромагнитной волне движение конца вектора Е (а, следовательно, и Н) можно охарактеризовать одним из перечисленных выше законов, то свет будет поляризован; в противном случае мы имеем дело с неполяризованным светом. Такой свет называют также естественным. В естественном свете все направления колебаний вектора Е в плоскости, перпендикулярной направлению распространения света, равноправны (см. рис. 1.12).

Рис. 1.12.

Если свет имеет какое-то преимущественное направление колебаний векторов Е, но не исключительное, то такой свет называют частично поляризованным (см. рис. 1.13).

Рис. 1.13

Следствия:

1. любую плоско поляризованную волну можно представить как суперпозицию двух других плоско поляризованных во взаимноперпендикулярных плоскостях волн, колеблющихся в фазе или противофазе;

2. любую волну, поляризованную по кругу, можно представить как суперпозицию двух плоско поляризованных во взаимноперпендикулярных плоскостях волн, имеющих одинаковые амплитуды и колеблющиеся с разностью фаз, равной ±π/2;

3. любую эллиптически поляризованную волну можно представить как суперпозицию двух плоско поляризованных.волн, колеблющихся в общем случае с любой разностью фаз (в зависимости от ориентации эллипса), кроме равной πm, m - любое целое число.

Вопросы для самопроверки.

1. Какими физическими величинами характеризуется электромагнитная волна?

2. Нарисуйте и объясните мгновенное расположение векторов физических величин и направления распространения электромагнитного излучения.

3. Объясните понятие "поляризация".

4. Дайте определение плоской векторной поперечной синусоидальной волны.

5. Как в общем случае поляризована векторная синусоидальная волна?

6. Объясните, как в электромагнитной эллиптически поляризованной волне реализуется тот факт, что вектора Е, Н и направление движения луча всегда образуют правую тройку векторов.

7. Какова разность фаз колебаний проекций вектора Е в эллиптически поляризованной волне?

8. Дайте определение волны с круговой поляризацией.

9. Какими свойствами должны обладать проекции вектора Е, чтобы электромагнитная волна была поляризована по кругу? Нарисуйте колебания этих проекций.

10. Дайте определение линейно (плоско) поляризованной волны.

11. Нарисуйте всевозможные колебания проекций вектора Е в линейно поляризованной волне. Какова может быть разность фаз колебаний проекций вектора Е.

12. Какой свет называется естественным. Какой свет называется частично поляризованным.