
Переходная характеристика
Переходной характеристикой (переходной
функцией)![]() называется реакция системы (при нулевых
начальных условиях) на единичный
ступенчатый сигнал (единичный скачок)
называется реакция системы (при нулевых
начальных условиях) на единичный
ступенчатый сигнал (единичный скачок)
![]()
![]()
Импульсная и переходная функции связаны выражениями
![]() ,
,![]() .
.
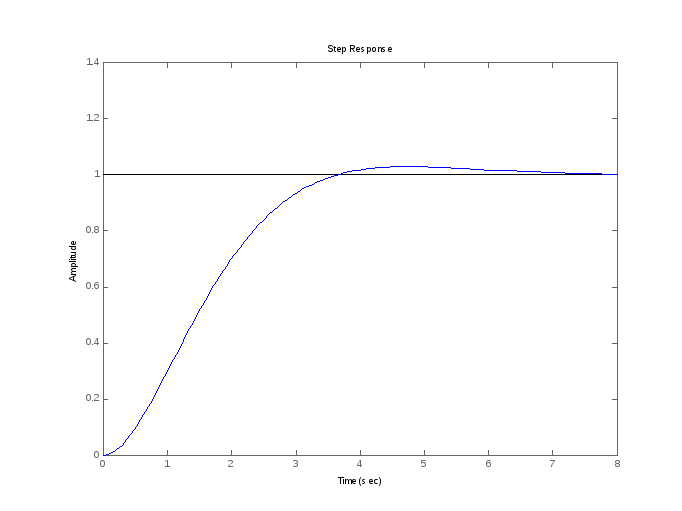
Для систем без интеграторов переходная
характеристика стремится к постоянному
значению. Переходная характеристика
системы с дифференцирующим звеном
(числитель передаточной функции имеет
нуль в точке
![]() )
стремится к нулю. Если система содержит
интегрирующие звенья, переходная
характеристика асимптотически стремится
к прямой, параболе и т.д., в зависимости
от количества интеграторов.
)
стремится к нулю. Если система содержит
интегрирующие звенья, переходная
характеристика асимптотически стремится
к прямой, параболе и т.д., в зависимости
от количества интеграторов.
По определению предельное значение
переходной функции
![]() при
при![]() есть статический коэффициент усиления:
есть статический коэффициент усиления:
![]() .
.
Эта величина имеет смысл только для устойчивых систем, поскольку при неустойчивости переходный процесс не сходится к конечному значению.
Е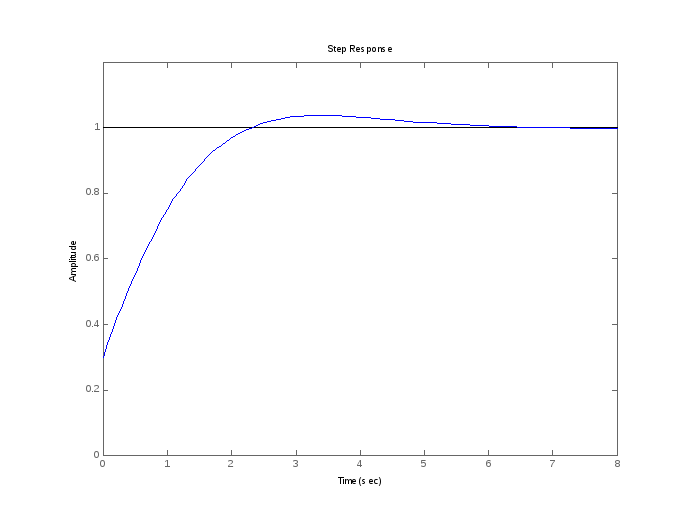 сли
передаточная функция правильная, но не
строго правильная (матрица
сли
передаточная функция правильная, но не
строго правильная (матрица![]() модели в пространстве состояний не
равна нулю), скачкообразное изменение
входного сигнала мгновенно приводит к
скачкообразному изменению выхода.
Величина этого скачка равна отношению
коэффициентов при старших степенях
числителя и знаменателя передаточной
функции (или матрице
модели в пространстве состояний не
равна нулю), скачкообразное изменение
входного сигнала мгновенно приводит к
скачкообразному изменению выхода.
Величина этого скачка равна отношению
коэффициентов при старших степенях
числителя и знаменателя передаточной
функции (или матрице![]() модели в пространстве состояний).
модели в пространстве состояний).
П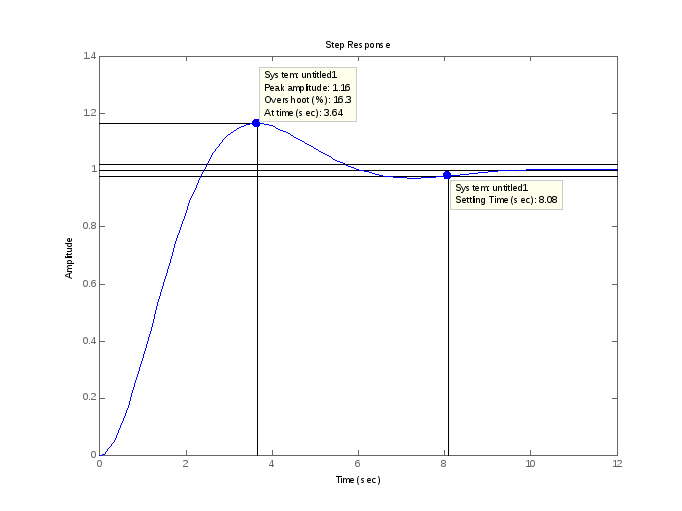 о
переходной характеристике можно найти
важнейшие показатели качества системы
– перерегулирование (overshoot)
и время переходного процесса (settling
time).
о
переходной характеристике можно найти
важнейшие показатели качества системы
– перерегулирование (overshoot)
и время переходного процесса (settling
time).
Перерегулирование определяется как
![]() ,
,
где
![]() – максимальное значение функции
– максимальное значение функции![]() ,
а
,
а![]() – установившееся значение выхода.
– установившееся значение выхода.
Время переходного процесса– это время, после которого сигнал выхода отличается от установившегося значения не более, чем на заданную малую величину (в средеMatlab по умолчанию используется точность 2%).
Частотная характеристика
При подаче на вход линейной системы
гармонического (синусоидального) сигнала
![]() с
частотой
с
частотой![]() (она измеряется в радианах в секунду),
на выходе будет также гармонический
сигнал той же частоты, но другой амплитуды
и фазы4
(она измеряется в радианах в секунду),
на выходе будет также гармонический
сигнал той же частоты, но другой амплитуды
и фазы4![]() ,
где
,
где![]() – амплитуда и
– амплитуда и![]() – сдвиг фазы.
– сдвиг фазы.
Частотная характеристика определяется
как реакция системы на комплексный
экспоненциальный сигнал
![]() .
Для ее построения надо использовать
подстановку
.
Для ее построения надо использовать
подстановку![]() в передаточной функции
в передаточной функции![]() .
Выражение
.
Выражение![]() называетсячастотной передаточной
функциейилиамплитудно-фазовой
частотной характеристикой системы(АФЧХ).
называетсячастотной передаточной
функциейилиамплитудно-фазовой
частотной характеристикой системы(АФЧХ).
Зависимость модуля величины
![]() от частоты называетсяамплитудной
частотной характеристикой(АЧХ), а
зависимость аргумента комплексного
числа (фазы)
от частоты называетсяамплитудной
частотной характеристикой(АЧХ), а
зависимость аргумента комплексного
числа (фазы)![]() от частоты –фазовой частотной
характеристикой(ФЧХ):
от частоты –фазовой частотной
характеристикой(ФЧХ):
![]() .
.
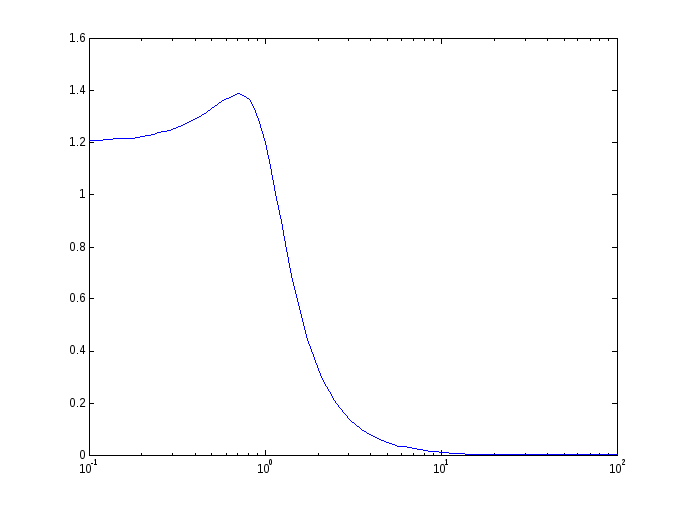
АЧХ показывает, насколько усиливается амплитуда сигналов разных частот после прохождения через систему, а ФЧХ характеризует сдвиг фазы сигнала.
![]()
![]()





![]()



![]()
Реальные объекты имеют строго правильную передаточную функцию, поэтому их АЧХ убывает с ростом частоты и асимптотически стремится к нулю. Говорят, что такой объект обладает свойством фильтра– фильтрует (не пропускает) высокочастотные сигналы (помехи, шумы измерений). Это свойство служит основой для использования метода гармонического баланса.
Частота, после которой значение АЧХ
уменьшается ниже 0 дБ (коэффициент
усиления меньше 1, сигнал ослабляется),
называется частотой срезасистемы![]() .Частота,
после которой значение АЧХ падает ниже
-3 дБ (коэффициент усиления меньше,
чем 0.708), называетсяполосой пропусканиясистемы
.Частота,
после которой значение АЧХ падает ниже
-3 дБ (коэффициент усиления меньше,
чем 0.708), называетсяполосой пропусканиясистемы![]() .
Для ее вычисления используют команду
.
Для ее вычисления используют команду
>> b = bandwidth ( f )
Максимум АЧХ соответствует частоте, на
которой усиление наибольшее. Значение
АЧХ при
![]() равно усилению при постоянном сигнале,
то есть, статическому коэффициенту
усиления
равно усилению при постоянном сигнале,
то есть, статическому коэффициенту
усиления![]() .
Это следует и из равенства
.
Это следует и из равенства
![]() .
.
Для систем с интегрирующими звеньями
частотная характеристика стремится к
бесконечности при
![]() .
Это значит, что их выход бесконечно
увеличивается или уменьшается при
постоянном входном сигнале.
.
Это значит, что их выход бесконечно
увеличивается или уменьшается при
постоянном входном сигнале.
Чтобы построить частотные характеристики в Matlab,надо сначала создать массив частот в нужном диапазоне. Для этого можно использовать функцииlinspace(равномерное распределение точек по линейной шкале) иlogspace(равномерное распределение точек по логарифмической шкале). Команда
>> w = linspace (0, 10, 100);
строит массив из 100 точек с равномерным шагом в интервале от 0 до 10, а команда
>> w = logspace (-1, 2, 100);
– массив из 100 точек с равномерным шагом
по логарифмической шкале в интервале
от
![]() до
до![]() .
.
Частотная характеристика на сетке wдля линейной моделиf (заданной как передаточная функция, модель в пространстве состояний или в форме «нули-полюса») вычисляется с помощью функцииfreqresp:
>> r = freqresp(f, w);
Функция freqresp возвращает трехмерный массив. Это связано с тем, что она применима и для многомерных моделей (с несколькими входами и выходами), передаточная функция которых представляет собой матрицу. Первые два индекса обозначают строку и столбец в этой матрице, а третий – номер точки частотной характеристики. Для системы с одним входом и одним выходом удобно преобразовать трехмерный массив в одномерный командой
>> r = r(:);
Для вывода графика АЧХ на экран можно использовать команды Matlab
>> plot ( w, abs(r) );
>> semilogx ( w, abs(r) );
>> loglog ( w, abs(r) );
В первом случае масштаб обеих осей координат – линейный, во втором случае используется логарифмический масштаб по оси абсцисс (частот), в последнем – логарифмический масштаб по обеим осям. Для вычисления фазы (в градусах) используется команда
>> phi = angle(r)*180/pi;
после чего можно строить ФЧХ, например:
>> semilogx ( w, phi );
