Координаты векторов

Мы будем сначала рассматривать координаты векторов на прямой плоскости и в пространстве, на которых уже введена декартова система координат для точек. В дальнейшем мы рассмотрим более общее понятие координат вектора в произвольном базисе.

Координаты векторов на прямой.

Рассмотрим прямую, на которой введена система координат для точек (ось). Рассмотрим вектор на этой оси. Координатой этого вектора назовем число, равное, если направление векторасовпадает с направлением оси или равноев противном случае. (Координату нулевого вектора полагаем равной нулю.) Записьозначает, что векторимеет координату. Если известны координаты точеки, то очевидно, что.

Вектор на оси выражает смещение по оси, его координата – числовую величину этого смещения. Легко показать, что если и, а- число, то, и, то есть при сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число его координата умножается на это число.

Координаты векторов на плоскости.

Рассмотрим плоскость, на которой введена декартова система координат для точек. Рассмотрим вектор на этой плоскости.

Обозначим (проекцияна ось Ох) вектор, лежащий на оси абсцисс и соединяющий точкии, являющиеся, соответственно, проекциями точекина ось Ох. Пусть- это координата векторана оси Ох. Аналогично определяется(проекцияна ось Оу) вектор, лежащий на оси ординат и соединяющий точкии, являющиеся, соответственно, проекциями точекина ось Оу. Пусть- это координата векторана оси Оу. Координаты вектора- это упорядоченная пара чисел, записьозначает, что векторимеет координаты.

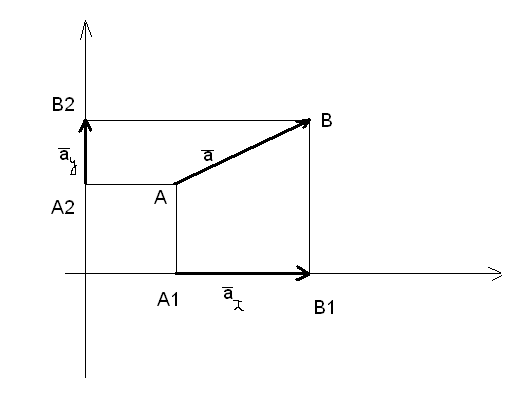
Пусть известны координаты точек и, тогда абсциссы точекисовпадают, соответственно, с абсциссами точеки, следовательно. Рассуждая аналогично, получим, что. Отсюда вытекает формула для координат вектора:

.

Если разместить вектор началом в начале координат, то можно увидеть, что.

Вектор на плоскости выражает смещение, его координаты – числовые величины этого смещения вдоль осей координат.

Рассмотрим два вектора ,и число, тогда

, и

,

то есть при сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число его координаты умножаются на это число.

Для доказательства этого достаточно представить векторы как суммы ,. Тогда (для суммы). Очевидно, что, и, поэтому. Аналогично доказываются остальные равенства (для разности и умножения на число).

Координаты векторов в пространстве.

Координаты векторов в пространстве вводятся аналогично тому, как мы это сделали для векторов на плоскости, только рассматриваются три оси. Поэтому вектор в пространстве будет иметь три координаты: .

Также как и для векторов на плоскости при сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число его координаты умножаются на это число.

Декартов базис.

Рассмотрим плоскость с введенной на ней декартовой системой координат. Рассмотрим вектор , направленный по оси абсцисс и имеющий единичную длину (единичный вектор оси абсцисс). Рассмотрим также вектор , направленный по оси ординат и имеющий единичную длину (единичный вектор оси ординат).

Рассмотрим теперь любой вектор на этой плоскости. Пусть известны координаты вектора. Тогда, легко понять, что

И обратно: если выполнено равенство , то.

Выше (тема 3) мы рассматривали понятие базиса во множестве столбцов чисел: это такой набор столбцов этого множества, из которого можно получить с помощью линейных операций все остальные столбцы этого множества, при этом каждый столбец базиса не может быть получен из остальных столбцов базиса с помощью линейных операций (базис состоит из линейно независимых столбцов).

Аналогично, векторы ,образуютбазис для всех векторов на плоскости. С помощью линейных операций можно получить из векторов ,любой вектор плоскости и, в то же время, нельзя выразить векторыидруг через друга. Этот базис, состоящий из векторов,, называется

декартовым базисом для векторов на плоскости.

В пространстве, помимо векторов и, рассматривается единичный вектор оси аппликат – вектор. Также легко убедиться, что векторимеет координатытогда и только тогда, когда имеет место равенство. Набор векторов,,образуетдекартов базис для векторов пространства.