Ранг множества столбцов (строк). Ранг матрицы.

Определение.

Набор столбцов А1, …, Аn образует базис в некотором множестве М столбцов чисел, если всякий столбец из множества М линейно выражается через столбцы А1, …, Аn, и столбцы А1, …, Аn линейно независимы.

Теорема. Любые два базиса в множестве столбцов М состоят из одинакового количества столбцов.

Доказательство теоремы прямо вытекает из следующей леммы:

Лемма: Если А1, …, Аnи В1, …, Вl– два линейно независимых набора столбцов длины k, и всякий столбец Вi(i= 1,... l) линейно выражается через столбцы А1, …Аn , то l меньше (или равно) n.

Доказательство леммы:

Предположим, что l > n . Так как Вiвыражается через А1, … Аn, то

В1 = а11 А1 + а12 А2 + … + а1n An,

B2 = a21 A1 + … + a2n An,

…

Bl = al1 A1 + … + aln An.

Рассмотрим линейную комбинацию столбцов В1 … Вl :

x1 B1 + ... + xlBl .

Докажем, что эта комбинация может быть нетривиальной и в тоже время равняться нулевому столбцу О.

х1 В1 + … + хl Bl = x1(a11 A1 + ... + a1n An) + x2(a21 A1 + ... + a2n An) + … + xl(al1 A1 + ... + aln An) = (a11 x1 + ... + al1 xl)A1 + (a1n x1 + ... + aln xl)An= О.

Рассмотрим систему однородных линейных уравнений

а11 х1 + … + al1 xl = 0

a12 x1 + ... + al2 xl = 0

…

a1n x1+ …+ alnxl = 0

Т.к. l > n эта система имеет нетривиальное решение.

Мы получили противоречие с условием линейной независимости столбцов В1, … Вl.

Лемма доказана.

Теперь, если А1, …, Аn и В1, …, Вl – два базиса во множестве М, ввиду леммы, l ≤ n и n ≤ l. Следовательно, l = n.

Определение. Рангом множества столбцов М называется число элементов его базиса. Обозначается rankM. Очевидно, что если М состоит из столбцов длины k, то rankM ≤ k, т.к. не бывает более чем k линейно независимых столбцов длины k.

Пример: Рассмотрим множество столбцов М:

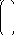
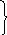1 3 4 2

М = 2 ; 1 ; 3 ; -1 .

-1 2 1 3

rankM = 2, т.к., например, 1-ые 2 столбца образуют базис в М. 2 остальные линейно выражается через них:

4 1 3

3 = 2 + 1 ,

1 -1 2

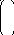
2 3 1

-1 = 1 - 2 .

3 2 -1

а11 … а1n

Определение. Рассмотрим произвольную матрицу А = …

ak1 ... akn

Минором порядка m (m ≤ min (k,n)) называется определитель квадратной матрицы, состоящей из элементов, стоящих на пересечении выбранных m строк и m столбцов.

Пример:

1 2 3 4

А = 5 6 7 8

9 10 11 12

24 1 2 7 8

6 8 , 9 10 , 11 12 и др. – миноры 2-го порядка

0. 3 4 1 2 3

5. 7 8 5 6 7

9 11 12 , 9 10 11 и др. – миноры 3-го порядка

Замечание. Ранг множества строк (одинаковой длины) определяется аналогично рангу множества столбцов.

Теорема (о ранге матрицы).

Для любой матрицы ранг множества её столбцов равен рангу с множества её строк и равен максимальному порядку отличного от нуля минора.

Доказательство:

Обозначим rстрок – ранг множества строк матрицы А

rстолб– ранг множества столбцов матрицы А

rминор – максимальный порядок отличного от нуля минора

Докажем, что rстрок = rминор, а затем, что rстолб= rминор.

Во-первых, rстрок≥ rминор, т.к. если l > rстрок, то любые l строк будут линейно зависимы, а, значит, в любом миноре порядка l строки будут линейно зависимы, и минор будет равен нулю, т.е. rминор< l.

Во-вторых, rстрок ≤rминор. Рассмотрим l = rстрок линейно независимых строк матрицы А. Пусть, для простоты обозначения, это будут первые l = rстрок строк:

(а11 … а1n),

(a21 … a2n),

…

(al1 … aln).

а11 … а1n

Обозначим А = … .

al1 … aln

Приведем матрицу А завершенным методом Гаусса к ступенчатому виду Аст

В ступенчатом виде последняя строка не может стать нулевой (состоять только из нулей), т.к. в этом случае получилось бы, что последняя строка

матрицы А линейно выражается через предшествующие строки, что

противоречит линейной независимости строк матрицы А . Следовательно в

Аст вообще нет нулевых строк. Напомним, что после применения завершенного метода Гаусса каждая строка имеет первый ненулевой элемент равный 1.

0 1 2 0 4 1 0 0

(Пример: Аст = 0 0 0 1 3 Мст = 0 1 0 )

0 0 0 0 1 , 0 0 1

Образуем минор Мст из столбцов, в которых стоят эти единицы. Этот минор является определителем единичной матрицы и равен 1, и имеет порядок равный l. Заметим, что элементарные преобразования строк не меняют

свойств миноров порядка l в А быть равными или не равными нулю.

Рассмотрим минор М (порядкаl) в матрице А, состоящий из элементов, стоящих на пересечении первых l строк и тех l столбцов, которые участвуют в миноре Мст. Минор М = 0. Следовательно rминор ≥rстрок.

rстрок ≥rминор

Итак rстрок ≤ rминор => rстрок = rминор.

Транспонируем матрицу А. Столбцы А перейдут в строки , а все миноры транспонируются и, следовательно, не изменят своих значений, т.е.rминор(A) = rминор(), ноrстолб(A) = rстрок().

По уже доказанному rстрок() =rминор().

Следовательно, rстолб(A)= rминор(A).

Теорема доказана.

Определение.Ранг матрицы – это число равное rминор(A) = rстрок(A) = rстолб(A). Обозначение: rankA.

Замечание. Ранг матрицы быстрее всего находится привидением её к ступенчатому виду. Элементарные преобразования не меняют ранга системы строк, ввиду доказанной выше леммы: новые строки линейно выражаются через старые строки (а старые через новые – все элементарные преобразования обратимы).

Ранг ступенчатой матрицы, а значит и исходной равен числу её ненулевых строк в ступенчатой матрице.

Пример: 2 -1 3 0 2

1 -2 1 3 1

Найдите ранг матрицы А = 3 -3 4 3 3

1 1 2 -3 1

Решение: Приведем А к ступенчатому виду

2 -1 3 0 2 1 -2 1 3 1 (- 2) (- 3) (- 1) 1 -2 1 3 1

1 -2 1 3 1 2 -1 3 0 2 + 0 3 1 -6 0 (-1)

3 -3 4 3 3  3 -3 4 3 3 +  0 3 1 -6 0 +

1 1 2 -3 1 1 1 2 -3 1 + 0 3 1 -6 0 +

1 2 1 3 1

0 3 1 -6 0

0 0 0 0 0

0 0 0 0 0

Ответ: rankA = 2.