Система однородных

линейных уравнений.

Определение. Если в линейной системе все свободные члены равны нулю, то уравнения в системе называются однородными:

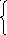а11 х1 + … + а1n xn = 0

…

ak1 x1 + ... + akn xn = 0.

Система линейных однородных уравнений всегда имеет тривиальное решение: х1 = 0

х2 = 0

…

хn= 0

Утверждение. Если в системе линейных однородных уравнений число уравнений меньше числа неизвестных, то эта система имеет нетривиальное решение.

Доказательство: Действительно, в этом случае система имеет бесконечное число решений, а, значит, все они кроме одного будут нетривиальными.

Утверждение. Система n линейных однородных уравнений с n неизвестными будет иметь нетривиальное решение тогда и только тогда, когда определитель матрицы этой системы будет не равен нулю.

Доказательство: Действительно, в этом случае система имеет бесконечное число решений, а, значит, все они кроме одного будут нетривиальными.

Линейная зависимость и независимость.

Рассмотрим n столбцов чисел длины k

а11 a12 a1n

А1 = … ; A2 = … ; … An = … .

аk1 ak2 akn

Линейной комбинацией этих столбцов называется выражение вида:

х1 А1 + х2 А2 + … + хnAn, где

х1, … хn – некоторые числа

Линейная комбинация называется тривиальной, если

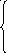х1 = 0

х2 = 0

…

хn= 0

Столбцы А1, … Аnназываются линейно зависимыми, если существует нетривиальная линейная комбинация этих столбцов равная нулевому столбцу

0

О = … , т.е. х1 А1 + х2 А2 + … + хnAn= 0, но не все числа х1, х2, …, хnравны

0

нулю.

Очевидно, что столбцы А1, … Аnбудут линейно зависимыми тогда и только тогда, когда система однородных линейных уравнений

a11 х1 + … + а1n xn = 0

…

ak1 x1 + ... + aknxn= 0

будет иметь нетривиальное решение.

Утверждение. Набор из n столбцов длины k будет линейно зависимым, если n > k.

Доказательство следует из предыдущего утверждения.

Таким образом, в линейно независимой системе из столбцов длины k может быть не больше k столбцов.

Пример:

1 0 0

Набор А1 = 0 ; А2 = 1 ; …. Аk= 0 линейно независим и содержит k

0 0 1

столбцов.

Действительно, равенствох1 А1 + … + хk Ak= 0

х1 = 0 x1

имеет место только при … , т.к. х1 А1 + … + хk Ak = … .

хk = 0 xk

Определение.

b1

Столбец В = …линейно выражается через столбцы А1, …, Аn, если В равен

bk

некоторой линейной комбинации этих столбцов А1 … Аn:

В = х1 А1 + … + хnAn.

Замечание. Таким образом, система линейных уравнений

а11 х1 + … + а1nxn = b1

…

ak1 x1 + … + aknxn = bk

совместна (т.е. имеет решение) тогда и только тогда, когда столбец свободных членов линейно выражается через столбцы матрицы системы.

Утверждение.

Набор столбцов будет линейно зависимым тогда и только тогда, когда хотя бы один из столбцов будет линейно выражаться через остальные.

Доказательство:

Если столбцы линейно зависимы, рассмотрим их нетривиальную линейную комбинацию х1 А1 + … + хn An = 0

Пусть, например, х1 = 0, тогда

А1 = - х2/x1*A2 - x3/x1*A3 - ... – xn/x1*An, т.е. А1 линейно выражается через остальные.

Замечание. Аналогично тому, как это сделано для столбцов, определяется линейная зависимость и независимость строк чисел.

Теорема. Рассмотрим определитель

а11 … а1n

= …

an1 ... ann

= 0  столбцы (и строки) определителя линейно зависимы

Доказательство:

Если = 0, система однородных уравнений

а11 х1 + … + а1n xn = 0

…

an1 x1 +… + ann xn = 0

имеет нетривиальное решение. А значит,столбцы определителя линейно зависимы.

Если столбцы линейно зависимы, то один (хотя бы) из столбцов линейно выражается через остальные. Вычтем из этого столбца эту линейную комбинацию остальных (т.е. его самого). Ввиду свойств определителя, определитель от этого не изменится. Однако, теперь появился столбец из нулей. Следовательно = 0.

Поскольку при транспонировании определитель не меняется, а строки становятся столбцами все сказанное для столбцов остается верным для строк определителя .