Тема 4. Понятие векторного пространства. Линейные операции над векторами Пространство Rn . Нормы в Rn . Скалярное произведение в Rn . Ортогональный и ортонормированный базисы.

Здесь будет рассматриваться обобщение результатов, которые мы получили, изучая понятие вектора в трехмерном пространстве.

Пусть имеется некоторое множество , содержащее элементы, которые мы будем называтьвекторами. На этом множестве определены две операции.

Первая операция – сложение. Это некоторый закон, по которому каждой паре векторов из множестваставится в соответствие векториз множества.

Кратко ее мы будем записывать так .

Вторая операция – умножение вектора на действительное число.

Эта операция – закон, по которому каждому вектору из множестваи любому действительному числуставит в соответствие некоторый векториз множества.

Кратко ее мы будем записывать так .

При этом эти операции удовлетворяют некоторым аксиомам, которые мы сейчас перечислим.

1.Коммутативность сложения: .

2.Ассоциативность сложения: .

3.Существование нуля. Предполагается, что среди элементов множества , существует элемент – обозначим его, и назовем нулевым вектором. Этот элемент обладает тем свойством, что если его сложить с любым векторомиз множества, то в результате мы получим тот же вектор. Мы здесь долго поясняли, а теперь давайте все, что было сказано, запишем кратко.

, такой что.

4.Существование обратного. Эта аксиома означает, что для любого вектора из множества, существует обратный вектор – его условно обозначимиз множества, такой что сумма векторовибудет равна нулевому вектору. Кратко это можно записать так.

, такой что.

Такая алгебраическая структура, удовлетворяющая четырем указанным аксиомам, называется коммутативной группой. Так вот с точки зрения операции сложения векторы образуют коммутативную группу.

Операция умножения вектора на действительное число также удовлетворяет некоторым аксиомам.

5. .

6.

7. .

8. .

Содержание этих аксиом очевидно и не требует особых пояснений.

В этом случае рассматриваемое множество называетсялинейным векторным пространством.

Докажите самостоятельно, что

В качестве примера, рассмотрим пространство, которое мы будем называть . Элементами этого пространствамы будем называть столбцы издействительных чисел.

.

Операции определим следующим образом.

Пусть ,, тогда,

Самостоятельно предлагается проверить, что введенные операции удовлетворяют указанным аксиомам.

Определение 1. Пусть имеется совокупность векторов .

Линейной комбинацией этих векторов называется выражение вида

.

Определение 2. Совокупность векторов , называется линейно независимой, если их линейная комбинация равна нулю тогда и только тогда, когда.

Определение 3. Размерностью векторного пространства называется максимальное число линейно независимых векторов.

Определение 4. Совокупность векторов , называется базисом линейного векторного пространства, если данная совокупность является линейно независимой и любой вектор пространства может быть выражен в виде линейной комбинации базисных векторов.

Размерностью линейного пространства называется число векторов его базиса (можно доказать, что любые два базиса данного линейного пространства состоят из одинакового числа векторов).

В рассмотренном выше примере пространства векторы

, ,…,образуют базис.

То, что они линейно независимы, предоставим вам доказать самостоятельно.

А любой вектор

представим в виде .

Пусть имеется базис . Тогда любой вектор представим в виде. Набор чиселназывается координатами векторав базисе, а векторыназываются составляющими векторав базисе .

Докажем, что координаты определены однозначно.

Пусть имеем

.

Тогда получаем

. А так как векторы линейно независимы, то . То есть соответствующие координаты равны.

Выбор базисных векторов достаточно произволен. Если мы исследуем конкретный вектор, то вектору безразлично, какой мы выбрали базис. При этом для нас его координаты будут различными в различных базисах. Следовательно, должен существовать способ преобразования координат вектора при переходе к другому базису.

Пусть система векторов образует базис в пространстве линейном векторном пространстве . Тогда любой векторэтого пространства может быть представлен в виде. Символически это будем представлять как вектор-столбец координат или, что тоже самое, матрицу размерностивида

. Указанный базис будем называть старым, и координаты также будем называть старыми.

Предположим, что имеется другой базис этого пространства , который назовем новым. Тот же векторв новом базисе представляется в виде. Вектор столбец его координат в новом базисе имеет вид.

Подчеркнем еще раз. Вектор один и тот же. Но поскольку базисы разные, то и координаты разные. Попытаемся связать координаты одного и того вектора в разных базисах.

Новые базисные векторы имеют какие-то координаты в старом базисе.

Пусть , где. То есть базисные векторы нового базиса представимы в старом базисе в виде вектор столбцов вида

.

Тогда вектор представим в виде. Подставляя выражения новых базисных векторов через старые, получаем

. Или, перегруппировав слагаемые, получаем

. С другой стороны . Но поскольку коэффициенты при базисных векторах (координаты вектора в базисе) должны быть одинаковы, то имеем

. Это соотношение и представляет формулу перехода от одних координат к другим. Запишем эту формулу красивее.

Для этого введем матрицу T размерности () вида

, которую мы будем называть матрицей перехода.

Заметим, что столбец с номером матрицы перехода представляет собой столбец координат базисного вектора с номеромнового базиса в старом базисе.

Тогда (если мы, конечно, помним правило умножения матриц) можно увидеть, что вектор столбец «старых» и «новых» координат связаны соотношением

, которое символически запишем в виде

Новые координаты через старые могут быть выражены соотношением

, где - обратная матрица.

До сих пор мы не касались вопросов длин векторов, углов между ними, то есть вопросов, связанных с метрикой пространства.

Предположим, что в векторном пространстве введено некоторое правило, по которому паре векторов ставится в соответствие действительное число. Это правило будем называть скалярным произведением и обозначать. При этом это правило удовлетворяет четырем аксиомам.

1. при этомтогда и только тогда, когда.

2. .

3. .

4. .

В частности в пространстве скалярное произведение определим следующим образом .

Если ,, то

Самостоятельно предлагается проверить, что введенная операция удовлетворяют указанным аксиомам.

Вместо слова длина вектора будем употреблять слово норма вектора, и обозначать ее будем символом .

Так вот в терминах скалярного произведения имеем =.

Косинус угла между векторами определим соотношением

.

Покажем, что введенный таким образом косинус угла удовлетворяет соотношению

Рассмотрим функцию вида=. В силу первого свойства скалярного произведениядля любых значений аргумента.

Используя свойства скалярного произведения, получаем

=, то есть данная функция является квадратной параболой. Но поскольку, то ее дискриминант меньше либо равен нулю. Значит

.

Следовательно

, что и требовалось доказать.

С помощью полученного соотношения докажем известное неравенство треугольников .

Имеем .

Поскольку , то

Что и требовалось доказать.

Проекцией вектора на векторназовем

.

Два вектора ибудем называтьортогональными, если их скалярное произведение равно нулю .

Базис будем называть ортогональным, если различные базисные векторы ортогональны друг другу, то есть при.

Базис будем называтьортонормированным, если номы всех базисных векторов равны единице и различные базисные векторы ортогональны друг другу, то есть , где- символ Кронекерапри,при.

Заметим, что базис ,,…,

Является ортонормированным базисом в в смысле введенного выше скалярного произведения.

Пусть в ортонормированном базисе ,. Тогда докажите самостоятельно, что:

1.

2.

3.

Заметим, что в случае перехода от одного ортонормированного базиса к другому, матрица перехода , в силу того, что ее столбцы это координаты новых базисных векторов в старом базисе, обладает интересным свойством: 1. сумма квадратов элементов любого столбца равна единице

2. сумма произведений соответствующих элементов различных столбцов равна нулю.

А это означает, что транспонированная матрица является обратной, то есть в этом случае.

В заключение рассмотрим пример.

Пример. Найти координаты вектора =в базисе векторов.

Пусть .

Тогда для определения неизвестных координат имеем систему трех уравнений с тремя неизвестными

Определитель системы равен

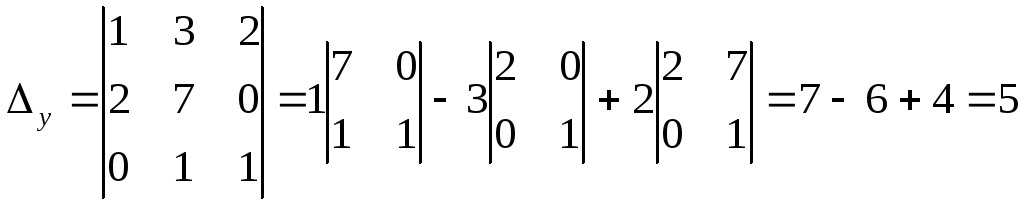
Тогда .

Имеем .