Общее уравнение линии второго порядка и его исследование

Определение. Общим уравнением линии второго порядка называется уравнение вида

, где .

Дальше мы будем заниматься тем, что будем искать такую систему координат, что бы уравнение приняло наиболее простой вид.

Попытаемся повернуть систему координат на угол .

Пусть точка М имеет координаты в исходной ив повернутой системе.

Тогда имеем

Подставляя в уравнение линии, получаем

Данное соотношение перепишем в виде

где

Отметим, что при повороте системы координат, коэффициенты меняются, однако некоторые их комбинации остаются неизменными.

Можно показать, что

.

Такие комбинации называются инвариантами.

Мы уже говорили, что от выбора системы координат существенно может зависеть сложность понимания той или иной задачи. Во и в данной задаче выберем угол поворота таким, чтобы коэффициент при произведении стал равен нулю. Имеем

.

Выбрав угол поворота системы координат из данного условия, уравнение представим в виде

.

Теперь рассмотрим некоторые возможные случаи.

Случай 1. Из коэффициентов ни один не равен нулю. Это означает

.

Посмотрим, как изменится уравнение линии при параллельном переносе начала системы координат.

Пусть начало системы координат теперь находится в точке О с координатами . Точка М в прежней системе координат имела координаты, в новой. При этом между координатами имеется следующая связь

.

Подставляя в уравнение линии, получаем

Данное соотношение перепишем в виде

где

.

Выберем значения из условия обращения в ноль коэффициентов.

Имеем

;

Тогда уравнение линии примет вид

.

Рассмотрим различные возможные варианты.

Вариант I(1). Коэффициенты одного знака. Это означает, что

. Тогда не ограничивая общности можно положить .

Возможны следующие ситуации

I(1а). . Преобразуем уравнение к виду

.

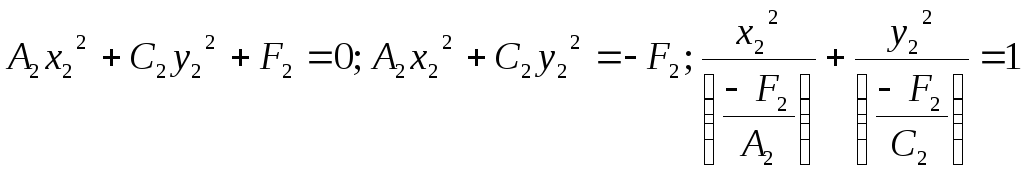Обозначим . Получаем- получили уравнение эллипса.

I(1б). . Преобразуем уравнение к виду

Этому уравнению удовлетворяет только точка . Иногда ее называют вырожденным эллипсом.

I(1в). . Тогда ни одна точка плоскости не удовлетворяет уравнению, то есть, имеем пустое множество, которое иногда называется мнимым эллипсом. Подведем первый итог. Случайбудем называть эллиптическим. В этом случае множество точек, удовлетворяющих этому уравнению, является либо эллипсом, либо точкой, либо пустым множеством.

Вариант I(2). Коэффициенты разных знаков. Это означает, что

. Тогда не ограничивая общности можно положить .

Возможны следующие ситуации

I(1а). . Преобразуем уравнение к виду

.

Обозначим . Получаем- получили уравнение гиперболы.

I(1б).). . Преобразуем уравнение к виду

.

Обозначим . Получаем- получили так же уравнение гиперболы.

I(1в). . Преобразуем уравнение к виду

. Обозначим . Получаем

Этому уравнению удовлетворяет пара пересекающихся прямых. I(1в). .

Подведем первый итог. Случай будем называть гиперболическим. В этом случае множество точек, удовлетворяющих этому уравнению, является либо гиперболой, либо парой пересекающихся прямых.

Рассмотрим второй случай, когда один из коэффициентов равен нулю.

Случай II. Из коэффициентов один равен нулю. Это означает

.

Для определенности положим .

В случае переноса начала системы координат в другую точку , как уже мы показывали, уравнение преобразуется к виду

где

.

Поскольку , то имеем

Где

.

Возможны различные варианты.

Вариант II(1). .

В этом случае выберем из условия.

Имеем ;

Тогда уравнение примет вид . Преобразуем его, где. Полученное уравнение является уравнением параболы.

Вариант II(2). . В этом случае, полагаем,. Тогда уравнение примет вид,

где ,

Не ограничивая общности можно считать, что .

Возможные ситуации.

II(2а). ,. Преобразуем уравнение;;;, где. Тогда этому уравнению удовлетворяют пара параллельных прямых.

II(2б). ,. Имеем. Тогда уравнению удовлетворяет пря мая. Иногда ее называют парой совпадающих прямых.

II(2в). ,.Имеем- на плоскости нет точек, удовлетворяющих данному уравнению. Имеем пустое множество. Иногда говорят, что уравнению удовлетворяют пара мнимых прямых.

Подведем итог. Случай будем называть параболическим. В этом случае множество точек, удовлетворяющих этому уравнению, является либо параболой, либо парой параллельных прямых, либо одной прямой, либо пустым множеством.

Рассмотрим примеры. Все вычисления проводим до трех знаков, а в конце округляем до двух.

Пример. Привести к простейшему виду уравнение линии второго порядка и сделать схематичный рисунок. .

Имеем А=1, В=-1, С=4. . Следовательно, линия эллиптического типа.

Определяем угол поворота

, ,

Заметим, что

Погрешность порядка точности вычислений.

Таким образом, уравнение линии в повернутой системе координат примет вид

.

Определяем координаты начала новой системы координат , где

;

Тогда

Тогда уравнение линии примет вид

.

Получили уравнение эллипса, с полуосями ,.

Осталось нарисовать рисунок.

Подробно представим последовательность действий.

Пример. Привести к простейшему виду уравнение линии второго порядка и сделать схематичный рисунок. .

Имеем А=1, В=2, С=-1. . Следовательно, линия гиперболического типа.

Определяем угол поворота

, ,

Заметим, что

Погрешность порядка точности вычислений.

Таким образом, уравнение линии в повернутой системе координат примет вид

.

Определяем координаты начала новой системы координат , где

;

Тогда

Тогда уравнение линии примет вид

.

Получили уравнение сопряженной гиперболы, с ,.

Осталось нарисовать рисунок.

Пример. Привести к простейшему виду уравнение линии второго порядка и сделать схематичный рисунок. .

Имеем А=1, В=-2, С=4. . Следовательно, линия параболического типа.

Определяем угол поворота

, ,

Заметим, что

Погрешность порядка точности вычислений. Однако в параболическом случае мы знаем, что один из коэффициентов должен точно равняться нулю.

Поэтому полагаем

Таким образом, уравнение линии в повернутой системе координат примет вид

.

Определяем координаты начала новой системы координат , где

В этом случае для определения имеем

Тогда

Тогда уравнение линии примет вид

.

Получили уравнение параболы.

Осталось нарисовать рисунок.

Теперь сделаем краткий обзор поверхностей второго порядка.

Эллипсоид.

Определение. Эллипсоидом называется поверхность, которая в некоторой прямоугольной декартовой системе координат задается уравнением

.

Форму этой поверхности исследуем методом сечений. Суть метода сечений состоит в том, что определяются линии, образованные пересечением некоторой серии плоскостей и данной поверхностью. Такая серия линий иногда позволяет наглядно представить форму поверхности. Отметим в начале, что эллипсоид, поверхность симметричная относительно всех координатных плоскостей. Поэтому достаточно построить его восьмую часть в области X>0, Y>0, Z>0.

Рассмотрим сечение плоскостью . Получаем- эллипс с полуосями. Аналогично сечениедает эллипсс полуосями. Теперь рассмотрим сечение. Получаем

Отметим, что , а в сечении - эллипс с полуосями,

Следующая поверхность – однополостный гиперболоид.

Определение. Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной декартовой системе координат задается уравнением

.

Форму этой поверхности исследуем методом сечений. Отметим, что однополостный гиперболоид, поверхность симметричная относительно всех координатных плоскостей. Поэтому достаточно построить его восьмую часть в области X>0, Y>0, Z>0.

Рассмотрим сечение плоскостью . Получаем- гипербола с полуосями. Аналогично сечениедает гиперболус полуосями. Теперь рассмотрим сечение. Получаем

Отметим, что , а в сечении - эллипс с полуосями,

Отметим, что уравнения так же являются уравнениями однополостного гиперболоида. Я надеюсь, вы самостоятельно можете представить их вид в соответствующей системе координат.

Отметим, что однополостный гиперболоид может быть собран из прямолинейных стержней, расположенных соответствующим образом. Этот факт используется в строительстве.

Двуполостный гиперболоид.

Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной декартовой системе координат задается уравнением

.

Форму этой поверхности исследуем методом сечений. Отметим, что двуполостный гиперболоид, поверхность симметричная относительно всех координатных плоскостей. Поэтому достаточно построить его восьмую часть в области X>0, Y>0, Z>0.

Рассмотрим сечение плоскостью . Получаем- гипербола с полуосями. Аналогично сечениедает гиперболус полуосями. Теперь рассмотрим сечение. Получаем

Отметим, что , а в сечении - эллипс с полуосями,

Отметим, что уравнения так же являются уравнениями двуполостного гиперболоида. Их расположение в координатных осях, я думаю, вы сможете представить самостоятельно.

Следующая поверхность – эллиптический конус.

Эллиптическим конусом называется поверхность, которая в некоторой прямоугольной декартовой системе координат задается уравнением

.

Форму этой поверхности исследуем методом сечений. Отметим, что эллиптический конус, поверхность симметричная относительно всех координатных плоскостей. Поэтому достаточно построить его восьмую часть в области X>0, Y>0, Z>0.

Рассмотрим сечение плоскостью . Получаем- пара пересекающихся прямых. Аналогично сечениедает пару пересекающихся прямых. Теперь рассмотрим сечение. Получаем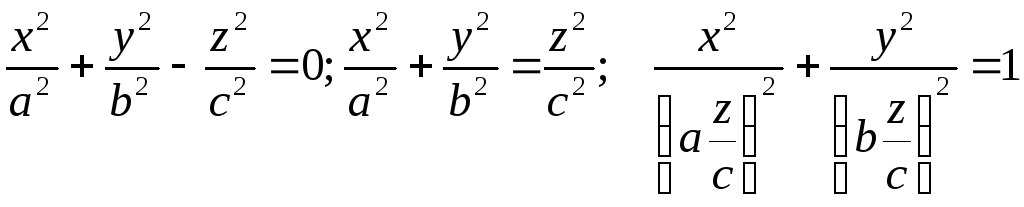

Отметим, что , а в сечении - эллипс с полуосями,

Отметим, что уравнения так же являются уравнениями эллиптического конуса.

Эллиптический параболоид.

Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной декартовой системе координат задается уравнением

.

Форму этой поверхности исследуем методом сечений. Отметим, что эллиптический параболоид, поверхность симметричная относительно координатных плоскостей X=0, Y=0, и при этом . Поэтому достаточно построить его четвертую часть в областиX>0, Y>0, Z>0.

Рассмотрим сечение плоскостью . Получаем- парабола. Аналогично сечениедает параболу. Теперь рассмотрим сечение. Получаем

Отметим, что , а в сечении - эллипс с полуосями,

Отметим, что уравнения

так же являются уравнениями эллиптического параболоида.

Гиперболический параболоид.

Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной декартовой системе координат задается уравнением

.

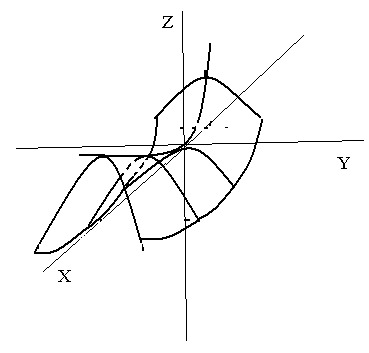
Форму этой поверхности исследуем методом сечений. Отметим, что эллиптический параболоид, поверхность симметричная относительно координатных плоскостей X=0, Y=0. Рассмотрим сечение плоскостью . Получаем- парабола. Сечениедает параболу. Поверхность напоминает седло. Эта поверхность также может быть собрана из прямолинейных стержней.

Отметим, что уравнения

так же являются уравнениями гиперболического параболоида.

Цилиндры.

Пусть на плоскости задано уравнение некоторой линии вида . Теперь будем рассматривать это уравнение в пространстве трех переменных. Мы обнаружим, что если точка плоскости А с координатамиудовлетворяет данному уравнению, то при любых значенияхz точка пространства М c координатами будет удовлетворять этому уравнению. При любыхz множество точек образуют прямую, параллельную осиZ, пересекающую плоскость XY в точке . Образованная поверхность называется цилиндрической с образующей, параллельной осиZ. Линия называется направляющей.

Эллиптический цилиндр с образующей параллельной оси Z.

Уравнение имеет вид . В плоскостиXY направляющая является эллипсом. Сечения плоскостью так же являются точно такими же эллипсами.

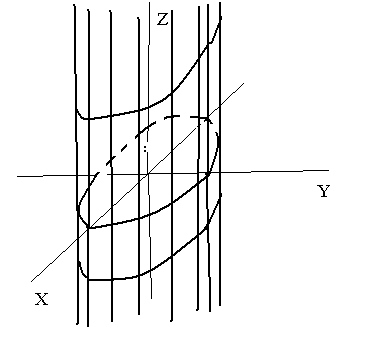
Уравнения эллиптических цилиндров, с образующими параллельными осям OX и OY вам предлагается записать самостоятельно.

Поскольку среди линий второго порядка, помимо эллипсов были еще гиперболы и параболы, то вы наверное уже догадались, что существуют гиперболические и параболические цилиндры. Их уравнения вам предлагается дома записать самостоятельно, а так же попытайтесь их изобразить схематично.

Пример. Привести уравнение поверхности второго порядка к простейшему виду, определить тип и сделать схематический рисунок.

Рассмотрим, как изменится уравнение поверхности, если начало системы координат сместить в точку . Связь координат в различных системах определяется соотношением.

Тогда уравнение поверхности примет вид

Перегруппируем слагаемые

Выберем из условия, что бы коэффициенты прибыли равны нулю.

Имеем: ;;.

Тогда уравнение примет вид

.

Преобразуем это выражение

.

Получили эллипсоид с полуосями .

Пример. Привести уравнение поверхности второго порядка к простейшему виду, определить тип и сделать схематический рисунок.

Рассмотрим, как изменится уравнение поверхности, если начало системы координат сместить в точку . Связь координат в различных системах определяется соотношением.

Уравнение поверхности примет вид

Перегруппируем слагаемые

. Выберем из условия, что бы коэффициенты прибыли равны нулю, а так же, что бы обратился в ноль свободный член.

Имеем: ;;

Тогда уравнение примет вид

, . Полученное уравнение, является уравнением эллиптического параболоида.

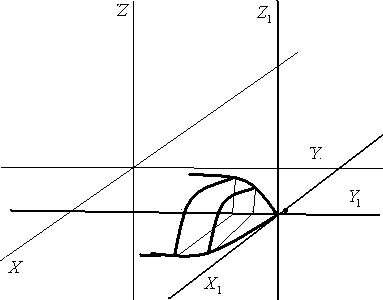
Последняя наша тема – это поверхность вращения. Предположим, что линия, заданная уравнением вращается относительно осиX. При этом образуется некоторая поверхность. Полученная поверхность называется поверхностью вращения. Попытаемся получить ее уравнение. Если точка лежит на поверхности, то ее расстояние до осиOX равно . Но с другой стороны поверхность образована вращением линиии, значит, это расстояние равно.

Следовательно, имеем .

Полученное уравнение и является уравнением поверхности вращения.