Уравнения прямой, проходящей через данную точку, параллельно данному вектору

Пусть прямая проходит через точку параллельно вектору .

Точка лежит на прямой тогда и только тогда, когда векторы иколинеарны. Векторыиколинеарны тогда и только тогда, когда их координаты пропорциональны, то есть

(4)

Полученная система уравнений (это пара уравнений, так как два знака равенства) задает искомую прямую и называется каноническими уравнениями прямой в пространстве.

Уравнения (4) представим в виде

, где принимает любые значения.

Следовательно, можем записать

, где (5)

Система (5) называется параметрическими уравнениями прямой в пространстве.

Рассмотрим пример. Найти уравнения прямой, проходящей через точки . Мы можем построить уравнения прямой, если знаем точку и параллельный ей вектор. Точек в наличии целых две. Но если две точки лежат на прямой, то вектор, их соединяющий будет параллелен этой прямой. Поэтому воспользуемся уравнениями (4), взяв в качестве вектора вектор. Получаем:

(6)

Уравнения (6) называются каноническими уравнениями прямой, проходящей через две данные точки.

Теперь выведем условия параллельности и перпендикулярности прямой и плоскости.

Пусть имеется уравнение плоскости (напомним , что вектор перпендикулярен даннойплоскости) и уравнение прямой

(напомним , что вектор параллелен даннойпрямой).

Прямая перпендикулярна плоскости тогда и только тогда, когда векторы иколинеарны. Следовательно, условие перпендикулярности прямой и плоскости имеет вид:

Прямая параллельна или лежит в плоскости тогда и только тогда, когда векторы иперпендикулярны. Соответствующее условие означает, что их скалярное произведение равно нулю. Имеем условие параллельности прямой и плоскости:

.

В заключение рассмотрим некоторые задачи.

Задача. Найти точку В, симметричную точке А , относительно плоскости, проходящей через точки,,.

Решение. Найдем уравнение плоскости. Векторы ибудут параллельны данной плоскости. Следовательно, в качестве вектора, перпендикулярного плоскости, можно взять вектор .

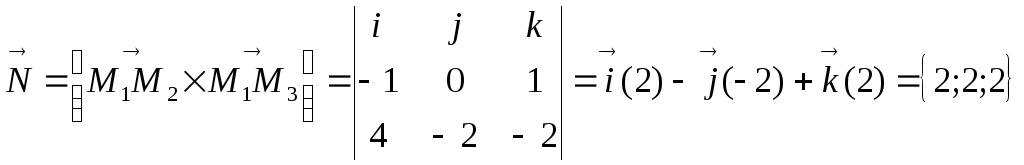Уравнение примет вид:

.

Теперь найдем уравнение прямой, проходящей через точку А, перпендикулярно плоскости. В качестве вектора , параллельного данной прямой, можно взять вектор .

Тогда параметрическое уравнение прямой имеет вид

Далее найдем точку S - проекцию точки А на плоскость, как пересечение прямой и плоскости. Фактически мы имеем систему четырех уравнений с четырьмя неизвестными.

Решаем эту систему. Подставляя из первых трех уравнений в последнее, получаем .

Тогда точка S имеет координаты ,.

Точка S является серединой отрезка АВ. Значит

Следовательно: .

Задача. Вершины треугольника АВС имеют координаты А(1;2;3), В(3;4;2), С(3;6;7). Найти параметрические уравнения высоты, медианы и биссектрисы, проведенных из вершины А.

Решение. Определим уравнение медианы АМ.

Точка М() середина отрезка ВС.

Тогда , . Следовательно, точка М имеет координаты M(3;5;9/2). Уравнение медианы на языке аналитической геометрии это уравнение прямой, проходящей через точку А(1;2;3) параллельно вектору ={2;3;3/2}. Тогда параметрическое уравнение медианы имеет вид

Уравнение высоты AS - это уравнение прямой, проходящей через точку А(1;2;3) перпендикулярно вектору ={0;2;5}, и лежащей в плоскости треугольника АВС. Поскольку прямая лежит в плоскости треугольника АВС, то ее направляющий вектор будет перпендикулярен к вектору

, перпендикулярному плоскости треугольника.

.

Поскольку вектор , направляющий вектор прямойBS перпендикулярен ={0;2;5} и, то в качестве вектораможет быть выбрано их векторное произведение

Тогда параметрическое уравнение высоты имеет вид

Для определения уравнения биссектрисы найдем вектор параллельный этой прямой. Для этого воспользуемся свойством диагонали ромба. Если от точки А отложить единичные векторы одинаково направленные с векторамии, то вектор, равный их сумме, будет параллелен биссектрисе. Тогда имеем=+.

={2;2;1}, , ={2;4;4}, .Тогда =Тогда уравнение искомой прямой имеет вид

Тема 3. Эллипс. Гипербола. Парабола. Определения, канонические уравнения. Исследование формы линий по их каноническим уравнениям. Общее уравнение кривой второго порядка и его упрощение с помощью поворота и параллельного переноса координатных осей.

Поверхности второго порядка. Цилиндрические поверхности. Поверхность вращения. Эллипсоид, однополостный и двуполостный гиперболоид. Эллиптический и гиперболический параболоиды. Исследование формы поверхностей методом сечений. Упрощение уравнений с помощью параллельного переноса координатных осей.

На этой лекции мы изучим линии, по которым двигаются планеты и другие космические объекты в нашей солнечной системе. Поскольку на космические объекты в нашей солнечной системе влияет еще притяжение других планет, то их траектории немного отличаются от таких линий, но отличаются не очень сильно, поскольку сила притяжения Солнца существенно выше силы притяжения других планет. Эти замечательные открытия сделал Иоганн Кеплер в самом начале 17 века, открыв попутно закон всемирного тяготения (обычно первенство в открытии этого закона неверно приписывают И. Ньютону, жившему и работавшему на полвека позже).

Начнем с эллипса.

Определение. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса равна постоянной величине, большей, чем расстояние между фокусами.

Нарисовать эллипс очень просто. Берем нерастяжимую нить, по длине равную сумме расстояний до фокусов. Концы нити закрепляем в фокусах. А далее ведем карандашом вдоль нити, оставляя ее все время натянутой.

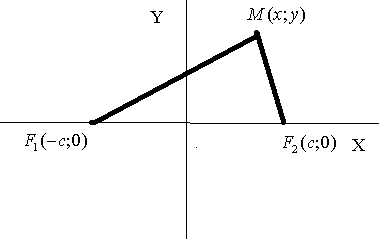
А теперь выведем каноническое уравнение эллипса. Обозначим расстояние между фокусами . Сумму расстояний до фокусов. Ось Х направим через фокусы, а осьY перпендикулярна оси Х и делит расстояние между фокусами пополам. Тогда точки - фокусы эллипса имеют координаты.. Пусть точка- лежит на эллипсе.

Тогда . Имеем

. Далее проведем цепочку преобразований.

Возводим в квадрат

Поскольку по условию , то обозначим.

Получаем

Окончательно получаем:

Полученное уравнение называется каноническим уравнением эллипса. Заметим, что в каноническом уравнении обязательно .

Строго говоря, мы еще не доказали, что полученное уравнение действительно является уравнением эллипса. Поскольку при выведении уравнения мы возводили в квадрат, то мы могли приобрести лишние точки. Но можно показать, что все точки, удовлетворяющие полученному уравнению, действительно лежат на эллипсе, то есть для них сумма расстояний до фокусов действительно равна .

Исследуем форму эллипса. Отметим, что эллипс – линия симметричная относительно всех координатных осей. Поэтому ее достаточно исследовать в первой четверти. В первой четверти имеем . Значениев первой четверти изменяется на отрезке.- убывающая функция, при этом. В точке- касательная параллельна оси ОХ, в точкекасательная параллельна оси. Величиныназываются соответственнобольшая и малая полуоси эллипса. Фокусы эллипса соответственно имеют координаты , где

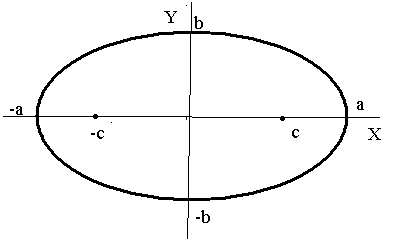
Иногда приходится иметь дело с уравнением вида , где. Это уравнение так же является уравнением эллипса, но не является каноническим, поскольку фокусы лежат на осиOY. Такой эллипс называется сопряженным.

В заключение отмечу, что в системе Коперника предполагалось движение планет по круговым орбитам. Первыми погрешность заметили мореплаватели. Потом Кеплер пришел к выводу, что планеты движутся не по круговым, а по эллиптическим орбитам, в фокусе которых находится солнце.

Следующая линия, это гипербола. По таким траекториям движутся кометы, которые один раз залетают в солнечную систему.

Определение. Гиперболой называется геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса равна по абсолютной величине постоянной, меньшей, чем расстояние между фокусами.

А теперь выведем каноническое уравнение гиперболы. Обозначим расстояние между фокусами . Разность расстояний до фокусов. Ось Х направим через фокусы, а осьY перпендикулярна оси Х и делит расстояние между фокусами пополам. Тогда точки - фокусы гиперболы имеют координаты.. Пусть точка- лежит на гиперболе.

Тогда . Имеем

. Далее проведем цепочку преобразований.

Возводим в квадрат

Поскольку по условию , то обозначим.

Получаем

Окончательно получаем

Полученное уравнение называется каноническим уравнением гиперболы.

Строго говоря, мы еще не доказали, что полученное уравнение действительно является уравнением гиперболы. Поскольку при выведении уравнения мы возводили в квадрат, то мы могли приобрести лишние точки. Но можно показать, что все точки, удовлетворяющие полученному уравнению, действительно лежат на гиперболе, то есть для них разность расстояний до фокусов действительно равна .

Исследуем форму гиперболы. Отметим, что гипербола – линия симметричная относительно всех координатных осей. Поэтому ее достаточно исследовать в первой четверти. В первой четверти имеем . Значениев первой четверти изменяется на отрезке.- возрастающая функция, при этом. В точкекасательная параллельна оси. Фокусы гиперболы соответственно имеют координаты, где

Исследуем характер поведения при . Найдем уравнения асимптот

Имеем .

Следовательно, с учетом симметрии относительно осей координат асимптотами являются прямые . Отметим, что эти прямые являются диагоналями прямоугольника, образованного прямыми

Иногда приходится иметь дело с уравнением вида . Это уравнение так же является уравнением гиперболы, но не является каноническим. Фокусы данной гиперболы лежат на осиY. Такая гипербола называется сопряженной.

Следующая линия – парабола.

Определение. Параболой называется геометрическое место точек плоскости, для которых расстояние до фиксированной точки плоскости, называемой фокусом параболы, равно расстоянию до фиксированной прямой, называемой директрисой параболы.

Каноническое уравнение параболы.

Выберем следующую систему координат. Пусть ось ОХ проходит через фокус параболы перпендикулярно директрисе. Ось OY делит отрезок между фокусом и директрисой на две равные части. При этом директриса лежит слева от оси OY, фокус справа. Расстояние между фокусом и директрисой обозначим . Тогда фокусF имеет координаты . Уравнение директрисы имеет вид. Пусть точкалежит на параболе.

Расстояние от этой точки до директрисы равно,

Расстояние от точки до фокуса.

Получаем

Уравнение называется каноническим уравнением параболы.

Отметим, что парабола симметрична относительно оси OY. В первой четверти имеем возрастающая функция. Точка О с координатами О(0;0) называется вершиной параболы.

Иногда приходится рассматривать уравнения вида ;;. Эти уравнения являются уравнениями параболы, но не являются каноническими.

В заключении я расскажу о любопытных оптических свойствах линий второго порядка. Представьте себе эллиптическое зеркало. Так вот, если источник света находится в одном фокусе, то лучи, отразившись, пересекутся в другом. И главное они придут туда за одно и то же время. А теперь, представьте, что в одном из фокусов устроен взрыв, то волна, отразившись, сфокусируется во втором фокусе. Я знаю, что в свое время была попытка создать аппарат для разрушения камней в организме человека.

В случае гиперболического зеркала продолжение отраженных лучей, вышедших из одного фокуса, пересечется в другом.

Для параболического зеркала, лучи, вышедшие из одного фокуса, отразившись, дают параллельный пучок. Где используется этот факт, я думаю, вы догадались.