Уравнение сферы

Пусть сфера имеет радиус , а ее центр находится в точке . Точка лежит на сфере тогда и только тогда, когда модуль вектораравен, то есть. А последнее равенство выполнено тогда и только тогда, когда

(1)

Уравнение (1) и является искомым уравнением сферы.

Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору

Пусть плоскость проходит через точку перпендикулярно вектору .

Точка лежит на плоскости тогда и только тогда, когда векторы иперпендикулярны. Векторыиперпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю, то есть. Тогда уравнение плоскости записываем в виде

(2)

Рассмотрим пример. Найти уравнение плоскости, проходящей через середину отрезка АВ перпендикулярно этому отрезку если координаты точек соответственно равны А(1;6;9), В(5;4;7).

Будем рассуждать следующим образом. Чтобы найти уравнение плоскости мы должны знать точку, через которую эта плоскость проходит, и вектор перпендикулярный этой плоскости. Вектором, перпендикулярным данной плоскости, будет вектор , поскольку, по условию задачи, плоскость перпендикулярна отрезку АВ. Точку определим из условия, что плоскость проходит через середину АВ. Имеем . Таким образоми уравнение примет вид

Выясним вопрос, проходит ли эта плоскость через точку М(7;3;0).

Имеем , значит, эта плоскость не проходит через указанную точку.

Решим еще одну задачу. Найти уравнение плоскости, проходящей через точку , параллельно векторам.

Чтобы найти уравнение плоскости, мы должны знать точку и вектор, перпендикулярный этой плоскости. Точка у нас имеется, а вот вектора не хватает. Но мы имеем в качестве компенсации два параллельных вектора. Теперь давайте вспомним свойства векторного произведения векторов. А оно гласит, что векторное произведение двух векторов направлено перпендикулярно плоскости, в которой эти векторы расположены. Следовательно, в качестве перпендикулярного вектора может быть взято векторное произведение векторов. Имеем

.

Уравнение плоскости примет вид

Еще один пример. Найти уравнение плоскости, проходящей через точки .

Как видим в наличии целых три точки и ни одного вектора. Но если вспомнить, что вектор, соединяющий две точки параллелен плоскости, в которой эти точки лежат, то задача сводится к предыдущей. Следовательно, плоскости параллельны вектор и вектор.

Тогда

.

Уравнение примет вид

Заметим, что нетрудно получить общую формулу уравнения плоскости, проходящей через три точки . Она получается из следующих соображений. Точка лежит в данной плоскости тогда и только тогда, когда векторы,

являются компланарными, а значит, их смешанное произведение равно нулю. Тогда получаем

или окончательно

. (3)

Общее уравнение плоскости

Определение. Общим уравнением поверхности первого порядка на плоскости называется уравнение вида , где.

Теорема. Всякая плоскость может быть задана в виде уравнения поверхности первого порядка, и всякое уравнение поверхности первого порядка является уравнением некоторой плоскости.

Первая часть этой теоремы доказывается просто. На всякой плоскости можно указать некоторую точку перпендикулярный ей вектор . Тогда, согласно (2), уравнение такойплоскости имеет вид . Обозначим. Тогда уравнение примет вид .

Теперь перейдем ко второй части теоремы. Пусть имеется уравнение , где. Будем считать для определенности.

Перепишем уравнение в виде;;.

Рассмотрим точку , где. Тогда полученное уравнение имеет вид , и является уравнениемплоскости, проходящей через точку перпендикулярно вектору .

Попутно мы доказали, что если имеется уравнение плоскости вида , то вектор перпендикулярен даннойплоскости.

Итак, уравнение вида называется общим уравнением плоскости в пространстве.

Далее выведем формулу вычисления расстояния от произвольной точки до плоскости, заданной общим уравнением.

Пусть имеется плоскость и точка. Требуется определить расстояние от указанной точки доплоскости.

Рассмотрим произвольную точку наплоскости. Имеем . Расстояниеот точкидоплоскости равно модулю проекции вектора на вектор , перпендикулярный данной плоскости.

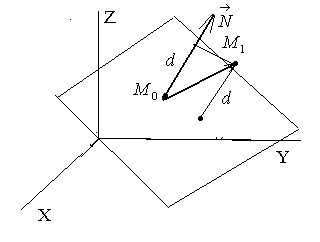
Имеем

,

преобразуя, получаем:

.

Пусть даны две плоскости, заданные общими уравнениями

, . Тогда векторы перпендикулярны первой и второй прямой соответственно. Уголмежду прямыми равен углу между векторами. Тогдаформула для определения угла имеет вид:

.

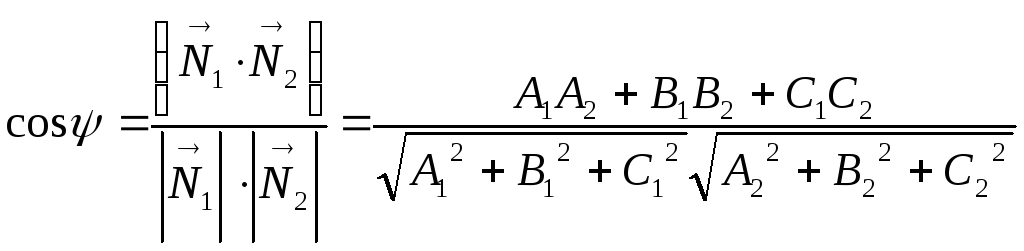Условие перпендикулярности плоскостей имеет вид:

.

Плоскости параллельны или совпадают тогда и только тогда, когда векторы колинеарны.

При этом условие совпадения плоскостей имеет вид: ,

а условие отсутствия пересечения записывается в виде: .

Последние два условия докажите самостоятельно.

Исследуем характер поведения плоскости по ее общему уравнению.

Пусть дано общее уравнение плоскости . Если , топлоскость проходит через начало координат.

Рассмотрим случай, когда ни один из коэффициентов не равен нулю . Уравнение перепишем в виде , ,

,

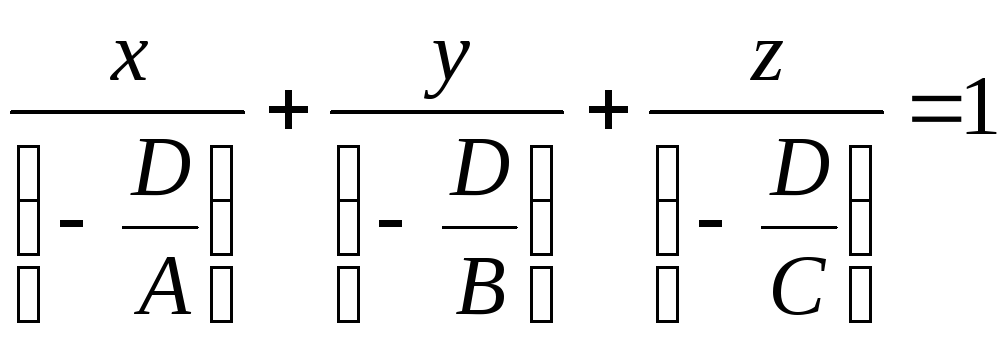где. Выясним смысл параметров . Найдем точки пересечения плоскости с осями координат. Приимеем, а приимеем_, при имеем.То есть- это отрезки, которые отсекает плоскость на координатных осях. Поэтомууравнение называется уравнением плоскости в отрезках.

В случае имеем,,,

где. То есть плоскость будет параллельна оси .

В случае имеем,,,

где. То есть плоскость будет параллельна оси .

В случае имеем,,,

где. То есть плоскость будет параллельна оси .

В случае имеем,,

где. То есть плоскость будет перпендикулярна оси .

В случае имеем,,

где. То есть плоскость будет перпендикулярна оси .

В случае имеем,,

где. То есть плоскость будет перпендикулярна оси .