Площадь параллелограмма, построенного на векторах, заданных своими координатами на плоскости

Предположим, что заданы координаты векторов :

. Тогда

Можно доказать, что , если пара векторов - правая, и , если пара векторов - левая.

Аналог смешанного произведения для векторов плоскости

Для векторов на плоскости операция, аналогичная смешанному произведению, будет операцией над двумя векторами.

Если два вектора на плоскости имеют координаты: , то естественно определить аналог смешанного произведения как число равное определителю:

Ввиду доказанной формулы для , получим геометрический смысл этой операции: , если пара векторов - правая и , если эта пара левая.

Аналогия простирается и дальше на пространство любой размерности.

Задача

Докажите, что аналог векторного произведения для векторов плоскости – это операция, совершаемая над одним вектором (результат обозначим). Она сводится к повороту этого вектора на против часовой стрелки.

Указание

Определите координаты вектора из условия:

для любого вектора

То есть мы как бы «делим» скалярно «смешанное произведение» на вектор .

ЗАДАНИЯ УПРАЖНЕНИЙ

1. Даны координаты точек на плоскости . Найти

а) координаты вектора ,

б) координаты точки - середины отрезка,

в) координаты точки , если,

г) координаты точки , если,

д) координаты точки , если.

2. Даны координаты векторов

Найти а) координаты ,

б) координаты ,

в) координаты .

3. Даны длины векторов и угол между ними

Найти а) скалярное произведение ,

б) скалярное произведение ,

в) длину вектора ,

г) проекцию вектора на направление другого вектора ,

д) угол между векторами и.

4. Даны координаты векторов

Выполнить задания пунктов а) - д) предыдущей задачи.

5. При каком значении параметра векторыибудут перпендикулярны?

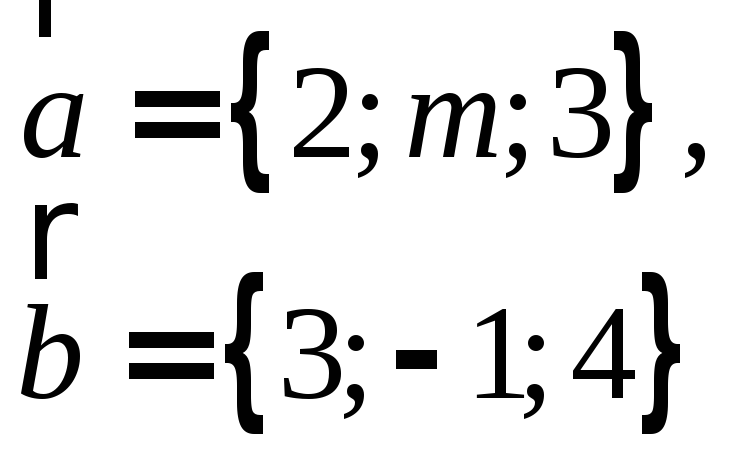
6. При каких значениях ивекторыибудут параллельны?

7. Даны длины векторов и угол между ними

Найти а) длину векторного произведения ,

б) длину векторного произведения .

8. Даны координаты векторов

Найти координаты векторного произведения .

9. Даны координаты вершин треугольника на плоскости

. Найти площадь треугольника .

10. Даны координаты вершин треугольника в пространстве

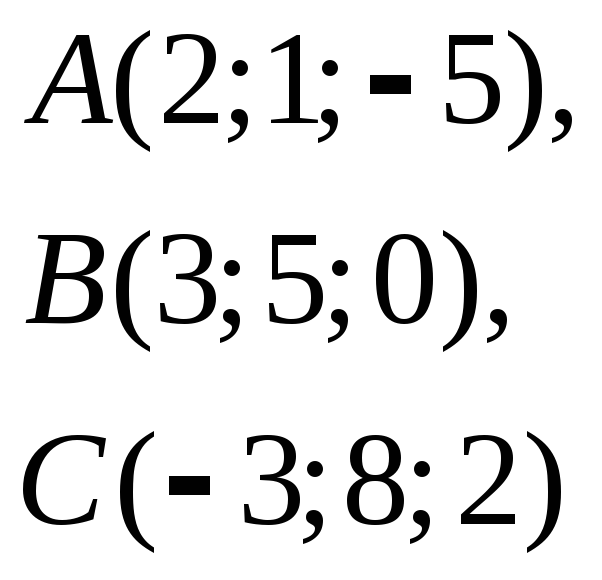. Найти площадь треугольника .

11. Даны координаты векторов в пространстве

Найти смешанное произведение .

12. Даны координаты вершин пирамиды в пространстве

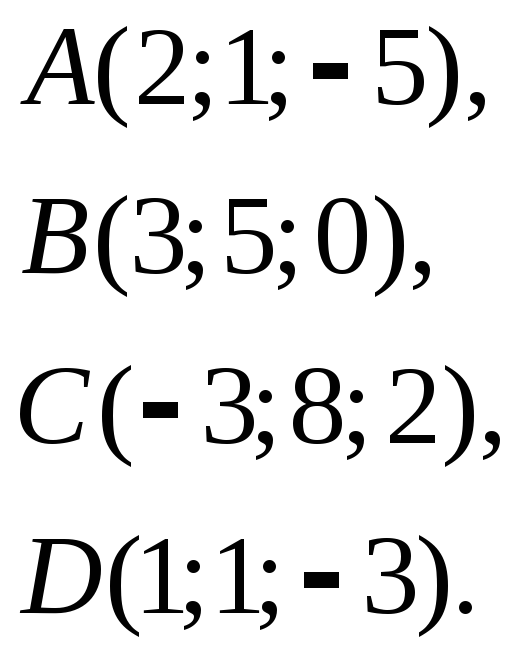. Найти а) объём пирамиды ,

б) длину высоты .

13. При каком значении параметра векторы,,будут компланарны?

14. При каком значении параметра точкибудут лежать в одной плоскости?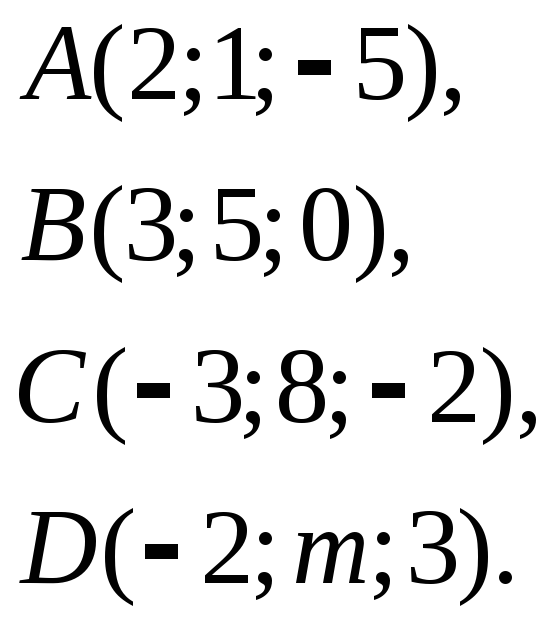

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Московский государственный университет

приборостроения и информатики

кафедра высшей математики

Головешкин В.А.

аналитическая геометрия прямой и плоскости, линии и поверхности второго порядка, основы теории линейных операторов и квадратичных форм

Редакция для дистанционного обучения:

Выборнов А.Н.

Москва 2011

Тема 1. Понятие об уравнении линии на плоскости. Уравнение окружности. Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору. Общее уравнение прямой и его исследование. Уравнение прямой, проходящей через данную точку параллельно данному вектору. Параметрические уравнения прямой. Уравнения прямой, проходящей через две данные точки. Уравнение прямой в отрезках. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Уравнение прямой, проходящей через данную точку с данными угловыми коэффициентами. Расстояние от точки до прямой.

Вначале дадим определение понятия уравнения линии на плоскости.

Пусть на плоскости задана некоторая линия.

Уравнение называется уравнением линии, если выполнены два условия:

1.для любой точки с координатами, лежащей на линии, выполнено, то есть ее координаты удовлетворяют уравнению линии;

2. любая точка , координаты которой удовлетворяют уравнению, лежит на линии.

Приведем пример.

Из курса элементарной математики известно уравнение биссектрисы первого и третьего координатного угла: , или то же самое.

Зададимся вопросом, будет ли уравнение уравнением данной прямой? Очевидно, что любая точка прямойбудет удовлетворять и уравнению. С другой стороны, точкаудовлетворяет уравнению, но не лежит на прямой. Следовательно, уравнениене будет уравнением исследуемой линии.