ВЕЧЕРНЕЕ 1 семестр 2012 / Решение экзаменационного теста

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Московский государственный университет

приборостроения и информатики

кафедра высшей математики

Выборнов А.Н.

ПОСОБИЕ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНАЦИОННОМУ ТЕСТИРОВАНИЮ ПО МАТЕМАТИКЕ ЗА 1 СЕМЕСТР

Москва 2002

Рассмотрим решения основных типов задач экзаменационного теста:

1. Решить матричное уравнение

Решение:

Найдем . Вычислим определитель матрицы .

Далее .

Ответ: .

2. Вычислить определитель .

Решение: Используя свойства определителей, вычтем из 3-й строки определителя 1-ю и 2-ю строки, определитель при таких преобразованиях не меняется.

Получим:

.

Разложим теперь определитель по 3-й строке:

.

Ответ: .

3. Сколько решений имеет система

Решение: В этой системе уравнений меньше чем неизвестных, поэтому возможна только одна из двух ситуаций: система не имеет решений или система имеет бесконечное множество решений. Для того чтобы выяснить, какая из ситуаций имеет место в данном случае, приведём расширенную матрицу системы к ступенчатому виду (используем метод Гаусса решения систем).

.

Мы видим, что в получившейся ступенчатой расширенной матрице есть длинная ступенька (подчёркнута два раза). Следовательно, система имеет бесконечное множество решений.

Ответ: бесконечное множество решений.

4. Решить систему (x, y - неизвестные) .

Решение: Используем метод Крамера:

Ответ: .

Решение: векторы параллельны тогда и только тогда, когда их координаты пропорциональны: .

Ответ: .

6. Найти сумму координат векторного произведения

Решение:

,

.

Ответ: .

7. При каком значении m точки A, B, C, D лежат в одной плоскости?

A(m; 1; 2), B(3;-1; 4), C(2; 1; 3), D(5; 1; 4).

Решение:

Точки A(m; 1; 2), B(3;-1; 4), C(2; 1; 3), D(5; 1; 4) лежат в одной плоскости тогда и только тогда, когда векторы компланарны.

компланарны тогда и только тогда, когда смешанное произведение

. Смешанное произведение - это определитель, у которого по строкам записаны координаты векторов :

. Разложим этот определитель по второму столбцу:

Ответ: .

8. Найти уравнение прямой, проходящей через точку А(2; -1) перпендикулярно прямой .

Решение:

Н

n={2;3}

о А(2;-1)

l: 2x+3y-4=0

ормальный вектор к прямой будет параллелен искомой прямой, то есть может служить направляющим вектором этой прямой. Поэтому используем каноническое уравнение:

Ответ: .

Решение: Используем условие параллельности прямых, заданных своими общими уравнениями:

В нашем случае:

Ответ: .

Решение: Вторая прямая задана параметрическими уравнениями. Найдём при каком значении параметра точка второй прямой попадает на первую прямую. Для этого выражения для и из второго уравнения подставим в первое уравнение:

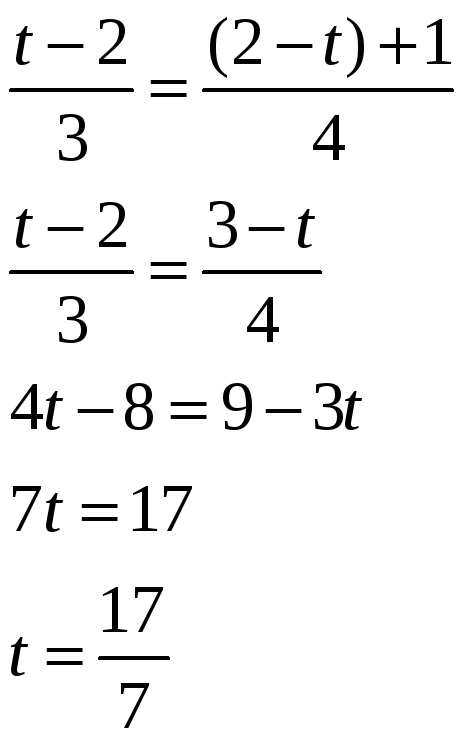
Теперь найдём координаты точки пересечения прямых:

Ответ: .

Решение:

Из уравнения плоскости получим координаты нормального вектора

. Этот нормальный вектор, перпендикулярный плоскости будет перпендикулярен и искомой плоскости. Запишем теперь уравнение искомой плоскости (нам известны координаты точки на плоскости и координаты нормального вектора):

Ответ: .

Решение:

Вектор будет параллельным искомой прямой.

Запишем теперь каноническое уравнение искомой прямой (известны координаты точки А на этой прямой и координаты направляющего вектора ):

Ответ: .

Решение: Эти три плоскости имеют ровно одну общую точку тогда и только тогда, когда система линейных уравнений

имеет ровно одно решение. Это будет выполнено тогда и только тогда, когда определитель матрицы системы будет не равен нулю. Итак:

Ответ: .

Решение: Переведём канонические уравнения прямой в параметрические уравнения:

Подставим выражения для из параметрических уравнений прямой в уравнение плоскости и найдём при каком значении прямая пересекает плоскость:

Найдём теперь координаты точки пересечения прямой и плоскости, для этого найденное значение подставим в параметрические уравнения прямой:

Ответ: .

Решение: Найдём точки пересечения плоскости и координатных осей:

С осью : подставим в уравнение плоскости . Получим: .

Итак, точка - точка пересечения с осью . Аналогично получим точку - точку пересечения с осью , и точку - точку пересечения с осью .

В пирамиде в основании лежит , причём это прямоугольный треугольник с катетами и .

Найдём площадь основания: .

Отрезок является высотой в пирамиде .

Найдём объём пирамиды: .

Ответ: .

Решение:

Найдём координаты нормального вектора к плоскости :

.

Найдём координаты направляющего вектора прямой :

.

Плоскость и прямая будут параллельны тогда и только тогда, когда векторы и будут перпендикулярны. Далее

Ответ: .

Решение:

Найдём любую точку на прямой , для этого положим в параметрических уравнениях этой прямой: . Получили точку .

Найдём расстояние от этой точки до плоскости , используя формулу:

Итак:

Ответ: .

Решение: В уравнении коэффициенты при и при , а также свободный член в правой части уравнения положительны. Уравнение можно привести к виду:

. Это уравнение эллипса.

Ответ: эллипс.

Решение: В уравнении присутствует переменная в первой степени, а переменные и во второй степени. Значит это уравнение параболоида. Кроме того, знаки коэффициентов при и при совпадают – значит это эллиптический параболоид.

Ответ: параболоид эллиптический.

Решение:

1способ. Матрица перехода от базиса к базису имеет вид:

.

Координаты вектора в старом и новом базисах связаны соотношением: .

Отсюда получим: . Найдём .

Найдём теперь новые координаты вектора :

.

2способ.

Обозначим неизвестные координаты вектора в новом базисе буквами и .

Тогда имеет место равенство:

Получим систему двух линейных уравнений с неизвестными и :

.

Решив систему, получим .

Ответ: