§3. Дисперсия. Моменты высших порядков

Определение.Моментом k-гопорядка называется выражение, вычисляемое по формулам:

а) для дискретной случайной величины:

, (6.3.1)

б) для непрерывной случайной величины:

. (6.3.2)

Для существования момента k-ого порядка необходимо:

а) для дискретной случайной величины — абсолютная сходимость ряда

, (6.3.3)

б) для непрерывной случайной величины — абсолютная сходимость интеграла

. (6.3.4)

Поскольку , то из существования момента к-го порядка вытекает существование момента (к-1)-го порядка и, следовательно, всех моментов меньших порядков.

Определение. Моментk-го порядка величиныназываетсяцентральным моментом k-го порядка.

Особую роль играет второй центральный момент, который называется дисперсией и обозначается .

Определение.Дисперсиейслучайной величиныназывается математическое ожидание квадрата отклонения случайной величины от своего математического ожидания:

. (6.3.5)

Свойствадисперсии.

1. Дисперсия постоянной величины равна нулю, т.е.

.

2. Дисперсия является неотрицательной величиной, т.е. .

3. Для любых действительных чисел исправедливо равенство

.

Доказательство. Из свойства 2 математического ожидания получаем:



4. .

Доказательство. Используя определение дисперсии и свойства 2 и 3 математического ожидания, получаем:



5. Если инезависимые случайные величины, дисперсия суммы случайных величин равна сумме дисперсий случайных величин, т.е.

.

Доказательство. Еслиинезависимые случайные величины, то и случайные величиныибудут независимыми. Тогда, используя свойства 2-4 математического ожидания, получаем:



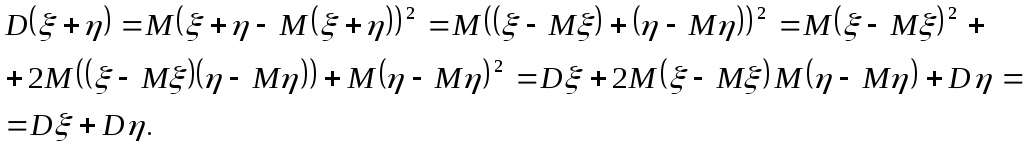
Очевидно, что дисперсия имеет размерность квадрата случайной величины. Для практических же целей удобно иметь числовую характеристику, размерность которой совпадает с размерностью.

Определение.Средним квадратичным отклонениемслучайной величины ξ называется выражение, вычисляемое по формуле:

. (6.3.6)

Пример 12. Найти дисперсию случайной величины, плотность которой имеет вид (равномерно распределенной на отрезке):

 Решение. Используя определение дисперсии, формулу для вычисления дисперсии непрерывной случайной величины (6.3.2) и результат примера 4, получаем:

.

Пример 13. Найти дисперсию случайной величины, распределенной по нормальному закону с параметрами(см. Пример 4).

 Решение. Используя определение дисперсии, формулу для вычисления дисперсии непрерывной случайной величины (6.3.2) и результат примера 5, получаем:

. (6.3.5)

Делаем замену или, при этом. В этом случае выражение (6.3.5) примет вид:



Пример 14. При условии примера 11 найти дисперсию случайной величины.

 Решение. Рассмотрим 1 способ нахождения дисперсии, используя ряд распределения случайной величины, найденный в примере 12,

и свойство 4 дисперсии, получим:

Напомним, что математическое ожидание было найдено в примере 12.

Перейдем ко второму способу нахождения математического ожидания случайной величины . Используя свойство 5 дисперсии случайной величины, получим:

, ,

, ,

, .

Глава 7. Элементы математической статистики §1. Основные понятия и основные задачи математической статистики

В математической статистике исследуются способы получения выводов на основе эмпирических (опытных) данных. Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения.

Определение. Генеральной совокупностьюназываются все возможные результаты наблюдений, которые могут быть сделаны при данном комплексе условий.

В некоторых задачах генеральную совокупность рассматривают как случайную величину . Примером генеральной совокупности может быть все население страны. В этой совокупности нас могут интересовать, например, возраст жителей. Другим примером генеральной совокупности являются детали, изготовленные на данном станке. Эти детали могут быть качественными и бракованными.

Определение. Выборочной совокупностью (выборкой) называется множество результатов, случайно отобранных из генеральной совокупности.

Выборка должна быть репрезентативной, т.е. правильно отражать пропорции генеральной совокупности. Это достигается случайностью отбора, когда все объекты генеральной совокупности имеют одинаковую вероятность быть отобранными.

Определение. Число объектов в совокупности (генеральной или выборочной) называется ее объемом.

Объем генеральной совокупности обозначим символом , а объем выборочной совокупности обозначим символом. При этом подразумевается, что.

Заметим, что сам процесс выбора можно осуществлять разными способами: выбрав объект и определив его значение, изымать объект и не допускать к последующим испытаниям (выборка без возвращения); после определения его значения объект возвращается в генеральную совокупность (выборка с возвращением). Очевидно, что при достаточно большом объеме генеральной совокупности исчезает различие между выборками с возвращением и без возвращения. Будем рассматривать случай бесконечно большого объема генеральной совокупности.

Основные задачи математической статистики:

1. Оценка значения неизвестной вероятности случайного события;

2. Определение неизвестной теоретической функции распределения;

3. Определение неизвестных параметров распределения теоретической функции распределения;

4. Проверка статистических гипотез;

5. Оценка зависимости.