Федеральное агентство по образованию

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Московский государственный университет

приборостроения и информатики

кафедра высшей математики

Манжиров А.В., Михин М.Н.

Теория вероятностей и математическая

статистика (решение задач)

Учебное пособие для студентов всех форм обучения для самостоятельной подготовки к выполнению контрольных работ.

Москва 2005

Редактор: Выборнов А.Н.

Глава 1. Случайные события и их вероятности

§1. События. Действия с событиями

Рассмотрим основные операции над событиями; они полностью соответствуют основным операциям над множествами.

Определение. Суммой событийиназывается событие, состоящее в наступлении хотя бы одного из событийили.

Определение. Произведением событийиназывается событие, состоящее в совместном (одновременном) наступлении этих событий.

Определение.Разностью событийиназывается событие, состоящее в том, что событиепроизошло, а событиене произошло.

Определение. Событие, состоящее в том, что событиене происходит, называетсяпротивоположнымсобытиюи обозначается.

Определение.Событиевлечет событие(является подмножеством множества), если из того, что происходит событие, следует, что происходит событие; записывают.

Определение.Если одновременнои, то в этом случае событияиназывают равносильными, при этом пишут.

Пример 4.Если— событие, состоящее в том, что взятое наудачу изделие первого сорта, а— изделие качественное (не брак), то в том событиевлечет событие:.

Свойства операций над событиями:

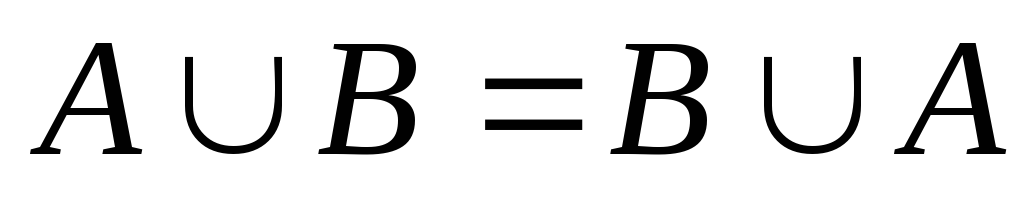• ,(коммутативность);

• ,(дистрибутивность);

• ,(ассоциативность);

• ,;

• ,;

• ,;

• ,,;

• ;

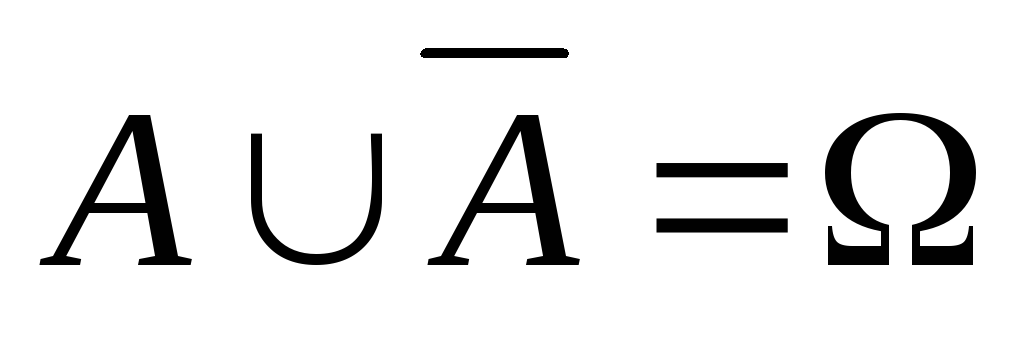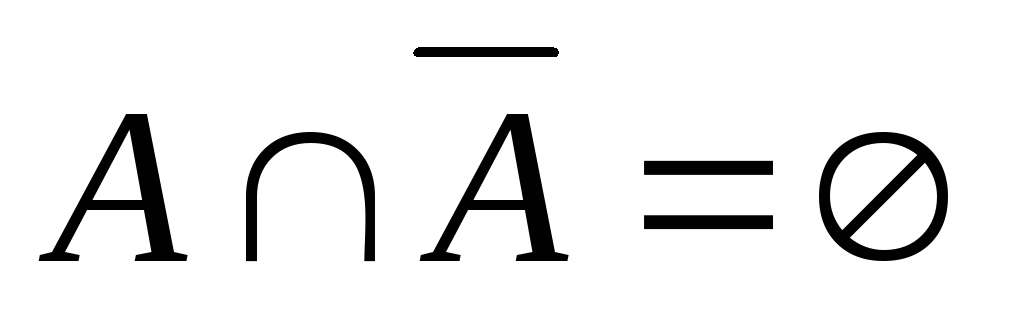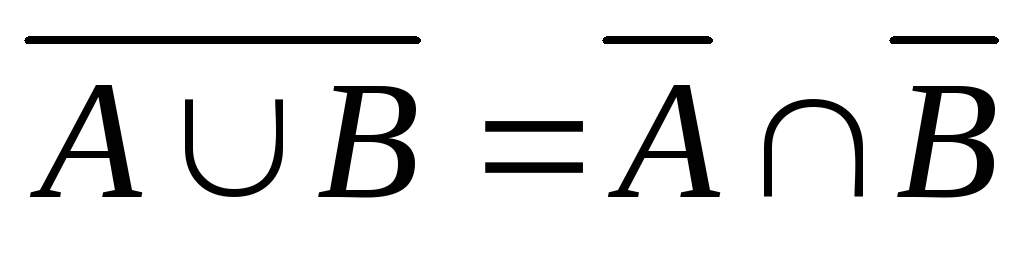• ,(законы де Моргана).

Определение.Событияназываютнесовместными, если при наступлении одного из событий, второе событие в данном испытании наступить уже не может.

Так, например, если при бросании игральной кости выпала грань «2», то это означает, что при том же бросании не могла появиться грань «4».

Определение.Событияобразуютполную группу событий, если в результате опыта, одно из событий обязательно происходит.

Например, при однократном бросании игральной кости полная группа попарно несовместных событий состоит из событий

,

которые состоят в выпадении 1,2,3,4,5,6 очков, соответственно.

Определение. Полная группа попарно несовместных, равновозможных событий образует множество элементарных исходов.Чаще всего в качестве элементарных исходов рассматривают множество простейших «неделимых» исходов некоторого опыта. Равновозможность означает намерение приписать исходам одинаковую вероятность. Здесь обычно руководствуются соображениями симметрии.

Элементарные исходы будем обозначать символами .

Определение.Пространством элементарных исходов называется множество всех элементарных исходов, которое будем обозначать символом.

Рассмотрим несколько примеров.

Пример 1. Описать пространство элементарных исходов при подбрасывании монеты.

 Решение. Очевидно, что при подбрасывании монеты возможны два элементарных исхода:

— появление «герба»;

— появление «решки».

Таким образом, пространство элементарных исходов содержит два элемента

.

Пример 2. Описать пространство элементарных исходов при подбрасывании игрального кубика.

 Решение. Очевидно, что при подбрасывании игрального кубика элементарными исходами является число, выпавших очков, т.е.

— выпало ровно очков;.

Таким образом, пространство элементарных исходов содержит шесть элементов

или.

Пример 3. На отрезке случайным образом отмечается точка. Описать пространство элементарных исходов.

 Решение. В этом случае результатом является координата, удовлетворяющая условию. Очевидно, что координатаменяется непрерывно, пространство элементарных исходов имеет вид

.

Пространство элементарных исходов имеет бесконечно много элементов.

Определение. Событие называетсядостоверным, если в результате опыта оно непременно должно произойти.

Достоверное событие обозначают символом , так как оно состоит из тех же элементарных исходов, что и пространство элементарных исходов. Событие, состоящее в появлении менее 7 очков при бросании игрального кубика, является достоверным.

Определение. Событие называетсяневозможным, если в результате опыта оно не может произойти.

Невозможное событие обозначают символом . Событие, состоящее в появлении 7 очков при бросании игрального кубика, является невозможным.

Замечание. Каждое случайное событиеможно рассматривать как некоторое подмножествомножества.

Определение.Элементарные исходы, принадлежащие подмножеству, называютсяблагоприятствующими событию.

При наступлении каждого элементарного исхода благоприятствующего событию , наступает и само событие, то есть каждый благоприятствующийисходвлечет событие .

Замечание.

Элементарными исходами суммы событий являются элементарные исходы, принадлежащие хотя бы одному из событийи.

Элементарными исходами произведения событий являются те элементарные исходы, которые одновременно принадлежат событиями.

Элементарными исходами разности событий являются те элементарные исходы события, которые не принадлежат событию.

Элементарными исходами противоположного события являются те элементарные исходы, которые не принадлежат событию.