3 - Графы / Лекция 22 Планарные графы

23 Лекция № 22. Планарные графы

Продолжительность: 2 часа (90 мин.)

23.1 Ключевые вопросы

23 Лекция № 22. Планарные графы 1

23.1 Ключевые вопросы 1

23.2 Текст лекции 1

23.2.1 Планарные графы 1

23.2.2 Условия планарности 2

23.2.3 Алгоритм построения плоского изображения графа 3

23.2.4 вопросы для контроля к п. 23.2 5

23.2 Текст лекции

23.2.1 Планарные графы

Планарный граф – это граф, допускающий укладку на плоскости, т.е. он может быть изображен на плоскости так, что никакие ребра не имеют общих точек, кроме своих вершин.

Изображение графа на плоскости с соблюдением этого условия называется плоским графом.

Планарность нужна, например, для реализации печатного монтажа, в процессе разработки которого схема устройства представляется в виде графа: элементы – вершины, связи между выводами элементов – ребра. Печатный монтаж выполняется в одной или нескольких плоскостях, называемых слоями, поэтому обычно возникают вопросы:

• граф планарен?

• Как получить планарное изображение графа?

Если граф не планарен, то приходится удалять (переносить на другой слой, на другую плоскость) отдельные ребра.

Минимальное число ребер, которое надо удалить для получения плоского изображения, называется числом планарности графа и обозначается (G). Для полных графов с

(K_n) = (n–3)(n–4)/2.

Из формулы следует, что при n = 4 (K₄) = 0. Для K₅ (K₅) = 1, следовательно, чтобы граф K₅ стал плоским, из него надо удалить одно ребро.

При перенесении на вторую плоскость, перенесенная часть может опять оказаться не плоской. Тогда отдельные ребра переносят на новую плоскость и т.д.

Минимальное число плоскостей, при котором граф разбивается на плоские части, называется толщиной графа и обозначается t(G).

Толщина произвольного графа удовлетворяет неравенству

t(G).

Здесь [x] – целая часть x.

Толщина полных графов удовлетворяет неравенству

t(K_n).

Например, для K₅ t(K₅) = 2.

23.2.2 Условия планарности

Ответ на первый вопрос: – Граф планарен? – можно получить, если воспользоваться условиями планарности.

У связного плоского графа с n3 число ребер m удовлетворяет условию

У связного плоского двудольного графа

Пример. Полный граф K₄ (рис. 23.1, а) – планарен?

В этом графе n = 4, m = 6.

Р исунок 23.1

Подставим эти значения в условие планарности

Условие выполняется. Следовательно, граф планарен. Действительно, граф K₄ можно представить так, как показано на рис. 23.1, б.

Из рисунка ясно, что граф K₄ планарен.

Пример. Полный граф K₅ (рис. 23.1, в) – планарен?

В этом графе n = 5, m = 10.

Подставим эти значения в условие планарности

Условие не выполняется. Следовательно, граф не планарен.

Пример. Двудольный полный граф К_3,3 (рис. 23.1, г) – планарен?

В этом графе n = 6, m = 9.

Подставим эти значения в условие планарности

Условие не выполняется. Следовательно, граф не планарен.

Из примеров видно, что расположить на плоскости без пересечения ребер можно далеко не всякий граф. А вот в трехмерном пространстве так может быть изображен любой конечный граф.

Доказательство простое.

Расположим все вершины на одной прямой рис. 23.2.

Р исунок 23.2

Построим m плоскостей на этой прямой, т. е. для каждого ребра свою плоскость.

Проведем ребра на своих плоскостях. Ребра не пересекаются (кроме как на своих вершинах).

Непланарность графов K₅ и К_3,3 используется для оценки планарности “больших графов”: граф не планарен, если он содержит подграфы вида K₅ или К_3,3, или сводимые к ним.

Грани плоского графа

У плоского графа кроме вершин и ребер можно выделить еще один геометрический образ – грань.

Область плоскости, ограниченная ребрами связного плоского графа и не содержащая внутри себя ни ребер, ни вершин, называется его гранью.

Внешняя неограниченная грань называется бесконечной гранью.

Например, граф на рис. 23.1, б обладает четырьмя гранями: f₁, f₂, f₃, f₄, где f₄ бесконечная грань.

У графа без циклов ровно одна грань – бесконечная. Не следует думать, что она какая–то исключительная. При укладке графа на сферу эта грань ничем не будет отличаться от других.

Число граней f в связном плоском графе определяется из соотношения

f = m – n + 2,

где n – число вершин, m – число ребер.

23.2.3 Алгоритм построения плоского изображения графа

Ответ на второй вопрос: – Как получить плоское изображение графа? – дает алгоритм, рассмотренный ниже.

Пусть задана часть G₁ = (V₁, E₁) графа G = (V, E).

Будем называть куском графа G относительно G₁:

1. ребро вместе с его концами, которые принадлежат V₁,

2. а также компоненту связности G’_i = (V’_i, E’_i) подграфа, порожденного подмножеством вершин V\V_l, дополненную всеми ребрами, инцидентными вершинам из V'_i, и всеми вершинами этих ребер, принадлежащими V₁ , которые называются «контактными точками»;

Алгоритм использует последовательный процесс присоединения к некоторому плоскому подграфу цепи , оба конца которой (и только они) – вершины . Эта цепь разобьет одну из граней на две.

В качестве начального плоского графа выбирают некоторый цикл графа G.

Чтобы перейти от подграфа к , предварительно рассматривают все куски P_j графа G относительно .

Грань f_k графа и кусок Р_j совместимы, если все его контактные точки принадлежат множеству вершин этой грани.

Для каждого куска определяем грани, которые с ним совместимы. Возможны три случая:

1. Некоторый кусок не совместим ни с какой гранью графа . Тогда граф не плоский.

2. Какой–либо кусок совместим с единственной гранью f_k графа . Тогда выберем в этом куске цепь такую, что оба ее конца (и только они) принадлежат 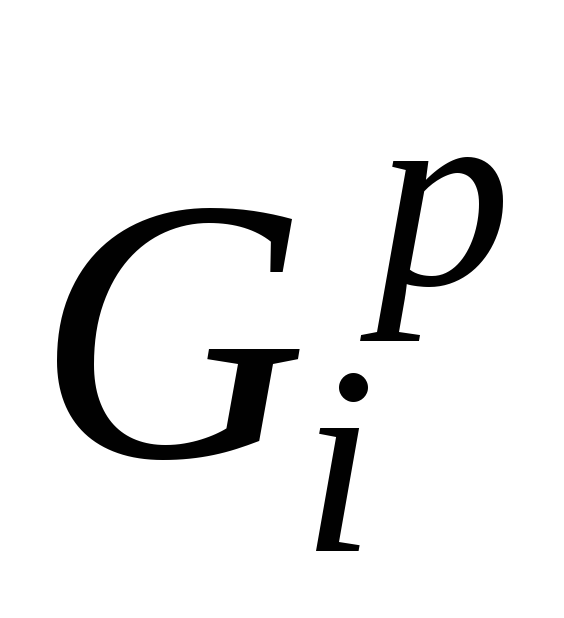. Дополняя ребрами и вершинами этой цепи, получаем , проводя 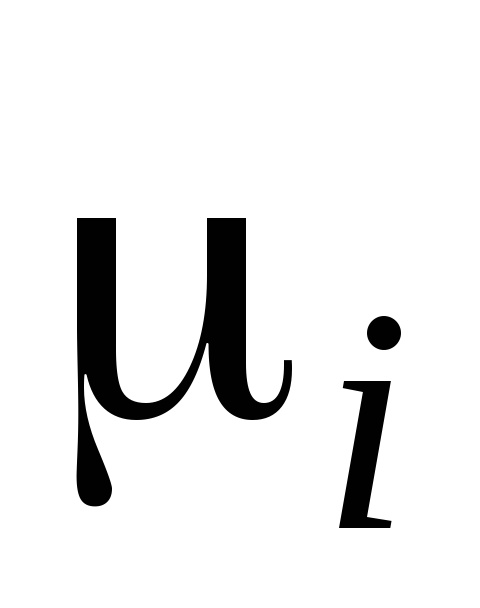внутри грани f_k.

3. Если каждый из кусков Р_j совместим, по крайней мере, с двумя гранями графа , то можно выбрать цепь в любом из кусков и действовать как в случае 2.

Пример. Проиллюстрируем этот алгоритм на примере графа G(V,E) рис. 23.3.

Р исунок 23.3

Шаг 1. Берем произвольный цикл, например u₀ = (1, 2, 6, 5, 1), представляющий плоский граф (рис. 23.4, а).

Грани:

A₀ — внешняя грань (1, 2, 6, 5, 1),

В₀ — внутренняя грань (1,2,6,5,1).

Куски графа G относительно :

Куски	Вершины куска	Контактные точки	Совместимые грани
P1	{1, 3, 5, 6}	{1, 5, 6}	A0 и B0
Р2	{1, 2, 4, 6}	{1, 2, 6}	A0 и B0

Шаг 2. Определяем . Все куски совместимы с двумя гранями (случай 3). Выбираем, например, цепь (1, 3, 5) из куска Р₁ и проводим ее в грани В₀. Эта грань в заменяется двумя гранями: В₁ – внутренней к (1, 3, 5, 1) и В₂ – внутренней к (1, 2, 6, 5, 3, 1) (рис. 23.4, б).

Куски G относительно :

Куски	Вершины кусков	Контактные точки	Совместимые грани
	{3, 6}	{3, 6}	В2
	{1, 2, 4, 6}	{1, 2, 6}	A0 и В2

Шаг 3. Определяем . Кусок Р₁ совместим лишь с одной гранью В₂ (случай 2). Цепь (3, 6) должна быть помещена в грань В₂, которую она разобьет на две грани: В₃ — внутреннюю к (3, 5, 6, 3) и В₄ – внутреннюю к (1, 2, 6, 3, 1) (рис. 23.4, в).

Р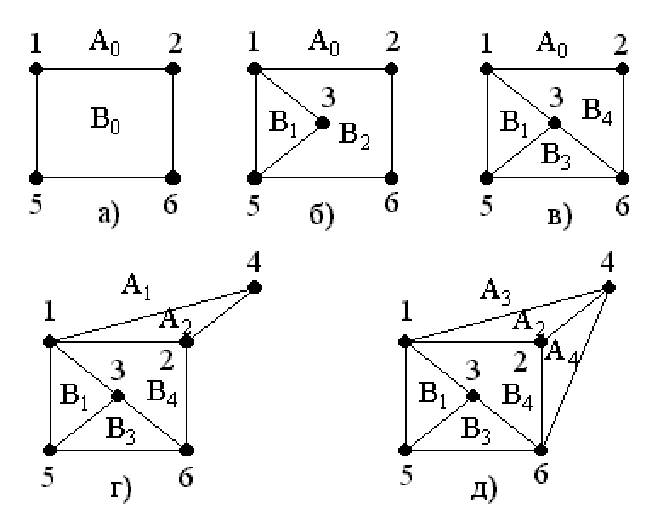 исунок 23.4

Куски G относительно :

Кусок	Вершины куска	Контактные точки	Совместимые грани
	{1, 2, 4, 6}	{1, 2, 6}	A0 и В4

Шаг 4. Определяем. Кусок совместим с двумя гранями A₀ и B₄ (случай 3). Возьмем, например, цепь (1, 4, 2) и поместим ее в грань A₀. Получаем две новые грани: A₁ – внешнюю к (1, 4, 2, 6, 5, 1) и А₂ – внутреннюю к (1, 4, 2, 1) (рис. 23.4, г).

Куски G относительно:

Кусок	Вершины куска	Контактные точки	Совместимые грани
	{4, 6}	{4, 6}	A1

Шаг 5. Определяем . Кусок совместим с одной гранью A₁ (случай 2). Помещаем единственную цепь (4, 6) в A₁ и получаем новые грани: A₃ – внешнюю к (1, 4, 6, 5, 1) и A₄ – внутреннюю к (2, 4, 6, 2) (рис. 23.4, д).

Таким образом, получаем плоское изображение графа G.

23.2.4 вопросы для контроля к п. 23.2

1. Что такое планарный граф?

2. Каковы условия планарности для произвольного графа?

3. Грань плоского графа – Что это такое ? Сколько граней у плоского графа?

4. Граф K₆ плоский? А K₇?

5. Что такое число планарности и толщина графа? Как их определить?

6. Какова идея алгоритма построения плоского изображения графа?