24 Лекция № 23. Двудольные графы

Продолжительность:2 часа (90 мин.)

24.1 Ключевые вопросы

24 Лекция № 23. Двудольные графы 1

24.1 Ключевые вопросы 1

24.2 Текст лекции 1

24.2.5 Двудольные графы 1

24.2.6 Минимальное покрытие двудольного графа 2

24.2.7 Паросочетание двудольного графа 6

24.2.8 Вопросы для контроля 8

24.2 Текст лекции

24.2.5 Двудольные графы

Двудольным графом называют такой граф G(XY,E), что

1. XY= ,

2. 

3. 

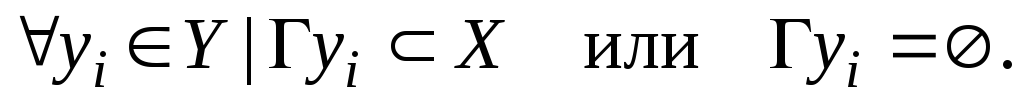
Пример двудольного графа и его матрица смежности показаны на рис. 24.1.

Рисунок 24.1

Свойства двудольного графа:

1. Множество вершин графа состоит из двух непересекающихся подмножеств таких, что внутри каждого подмножества нет смежных вершин.

2. На основании первого свойства вершины двудольного графа можно раскрасить двумя красками, поэтому такие графы называют бихроматическими.

3. Двудольный граф не имеет простых циклов нечетной длины.

Двудольные графы могут быть как ориентированными, так и неориентированными, однако большинство задач на двудольных графах ставятся и решаются так, как будто граф ориентирован. При этом предполагается, что начала дуг лежат в множестве X, а их концы в множествеY. Матрица смежности остается такой же, что и у неориентированного двудольного графа.

Рассмотрим некоторые задачи на двудольных графах.

24.2.6 Минимальное покрытие двудольного графа

Покрытием двудольного графа G(X,Y,E) называется такое подмножество дугW, что любая вершина графа инцидентна, по крайней мере, одной дуге изW(предполагается, что в графе нет изолированных вершин).

Например, для графа рис. 24.2 покрытием будет множество дуг

W = {(x₁,y₁), (x₂,y₄), (x₃, y₂), (x₄, y₃), (x₅, y₄), (x₅, y₅), (x₆,y₃)}.

Рисунок 24.2

В матрице смежности, показанной на рис. 24.2, дуги множества Wвыделены полужирным шрифтом.

Анализируя эту матрицу, можно определить покрытие графа как такой набор единиц, что каждая строка и каждый столбец содержат, по крайней мере, по одному элементу из этого набора.

По условию задачи требуется найти такое покрытие W₀, которое содержит минимальное количество дуг.

Алгоритм с использованием матрицы инцидентности графа

Для простоты будем рассматривать неориентированный двудольный граф, вершины которого обозначены натуральными числами 1, 2, 3,..., а ребра строчными буквами латинского алфавита.

Алгоритм:

1. Составляем матрицу инцидентности графа, в которой, как известно, число строк равно числу вершин графа, а число столбцов равно числу ребер графа. Каждое ребро инцидентно двум вершинам, поэтому в каждом столбце будет две единицы.

2. Для определения минимального покрытия вершин графа ребрами необходимо найти такую минимальную совокупность столбцов матрицы инцидентности (ребер), которая содержала хотя бы по одной 1 во всех строках, т.е. могла бы покрыть каждую вершину графа.

Для этого для каждой вершины (для каждой строки) записываем логическую сумму имен ребер, инцидентных вершине (имеющих 1 в строке вершины). Каждая сумма символизирует тот факт, что для покрытия вершины, чьим именем обозначена строка, нужно или ребро a, инцидентное вершине, или реброb, инцидентное вершине, и т.д.

3. Для покрытия графа надо покрыть и вершину 1, и вершину 2, и т.д. Поэтому из сумм предыдущего пункта, заменив союз И символом логического умножения, составляем логическое произведение.

4. полученное логическое произведение сумм преобразуется в дизъюнктивную форму и минимизируется. Терм с минимальным числом букв и будет представлять минимальное покрытие графа.

Пример. Дан граф рис. 24.3.

Найти минимальное подмножество ребер, инцидентных всем вершинам.

Составляем матрицу инцидентности графа (табл. 24.1).

Записываем для каждой вершины логическую сумму из имен инцидентных ей ребер.

Составляем логическое произведение полученных сумм, раскрываем скобки и минимизируем

(ab)(cd)(ac)(bd) =

= (acadbcbd)(abadbccd) =

= abcacdabcacdabdadabcdacd

abcabcdbcbcdabdabdbcdbcd=

= adbc.

Подмножество ребер adилиbспокрывает все вершины графа.

Рисунок 24.3

Таблица 24.1
	a	b	c	d
1	1	1	0	0
2	0	0	1	1
3	1	0	1	0
4	0	1	0	1

Данный алгоритм пригоден для любых графов и может быть применен для решения обратной задачи – определения вершинного покрытия графа, при котором определяется минимальное множество вершин инцидентных всем ребрам (дугам) графа.

Этот алгоритм по идее прост, однако, как видно из рассмотренного очень простого примера, его реализация достаточно сложна. Поэтому применяют другие алгоритмы, один из которых рассмотрен ниже.

Алгоритм с использованием матрицы смежности графа

Рассмотрим алгоритм построения минимального покрытия двудольного графа на примере графа G(X,Y,E), показанного на рис. 24.4.

Матрица смежности графа показана в табл. 24.2. (размер матрицы 6х 5: 6 = |X| =m– число вершин множестваX, 5 = |Y| =n– число вершин множестваY).

Алгоритм:

1. Сопоставим каждой строке матрицы смежности графа число F_i, равное сумме ее элементов, и каждому столбцу – числоG_j, равное сумме его элементов (соответствующие числа показаны справа и снизу таблицы).

Очевидно, что

.

2. Если

,

то множество дуг, соответствующих 1, дает минимальное покрытие.

Рисунок 24.4

Таблица 24.2

	y1	y2	y3	y4	y5	Fi
x1	1	1	0	0	0	2
x2	0	1	1	0	0	2
x3	0	0	1	1	1	3
x4	1	0	0	0	0	1
x5	1	0	0	1	0	2
x6	1	0	0	0	0	1
Gj	4	2	2	2	1

Если

,

то отмечаем последовательно в произвольном порядке символом * каждую из единиц, для которой F_i – 1>1 иG_j– 1>1, при этомF_iиG_jуменьшаем на 1.

Например, помечаем 1 на местах (x₁,y₁), (x₂,y₃), (x₅,y₄) в матрице табл. 24.2, получим матрицу, показанную в табл. 24.3.

Видим, эту операцию нельзя продолжить.

3. В каждой строке с F_i >1 ищем такую неотмеченную 1, что в содержащем ее столбцеkнайдется отмеченная 1, в строкеmкоторой есть либо неотмеченная 1 сG_j> 1, либо отмеченная 1.

Если найдена 1 с G_j> 1, то есть возможность увеличить число 1 с метками. Для этого помечаем найденную единицу с координатамиm,jи единицу с координатамиi,k.

Метку у единицы cкоординатамиk,mудаляем. ИзF_iиG_jвычитаем по 1.

Если в строке mнайдена отмеченная единица в столбцеjcG_j = 1 и этот столбец содержит также отмеченyю 1 в строкеn, то в строкеnищем либо неотмеченную 1 сG_j> 1, либо отмеченную 1 и т.д.

Если, действуя по этому алгоритму, невозможно больше отметить 1, то единицы без меток дают минимальное покрытие.

Таблица 24.3

	y1	y2	y3	y4	y5	Fi
x1	1*	1	0	0	0	1
x2	0	1	1*	0	0	1	m
x3	0	0	1	1	1	3	i
x4	1	0	0	0	0	1
x5	1	0	0	1*	0	1
x6	1	0	0	0	0	1
Gj	3	2	1	1	1
		j	k

В рассматриваемом примере последовательно получаем табл. 24.4 и табл. 24.5. В табл. 24.3, 24.4 и 24.5 пути поиска выделены полужирным шрифтом.

Таблица 24.4

	y1	y2	y3	y4	y5	Fi
x1	1*	1	0	0	0	1
x2	0	1*	1	0	0	1
x3	0	0	1*	1	1	2	i
x4	1	0	0	0	0	1
x5	1	0	0	1*	0	1	m’
x6	1	0	0	0	0	1
Gj	3	1	1	1	1
	j’			k’

Таблица 24.5

	y1	y2	y3	y4	y5	Fi
x1	1*	1	0	0	0	1
x2	0	1*	1	0	0	1
x3	0	0	1*	1*	1	1	i
x4	1	0	0	0	0	1
x5	1*	0	0	1	0	1	m’
x6	1	0	0	0	0	1
Gj	2	1	1	1	1
	j’			k’

Минимальное покрытие графа будет таким

W₀ = {(x₁,y₂), (x₂,y₃), (x₃,y₅), (x₄,y₁), (x₅,y₄), (x₆,y ₁)}.