1 - Множества / Лекция 7 Операции над отношениями

10

8 Лекция №7. Операции над отношениями представленными матрицами и графами¹

Продолжительность: 2 часа (90 мин.)

8.1 Ключевые вопросы

8 Лекция №7. Операции над отношениями представленными матрицами и графами 1

8.1 Ключевые вопросы 1

8.2 Текст лекции 1

8.2.1 Операции над отношениями представленными матрицами и графами 1

Вопросы для контроля 10

8.2 Текст лекции

8.2.1 Операции над отношениями представленными матрицами и графами

В Лекции № 5 мы рассмотрели операции над отношениями при их представлении подмножествами прямого произведения множеств M₁ х М₂ (или M ² при M₁ = М₂ = M). Теперь рассмотрим, как можно выполнить эти операции при представлении отношений матрицами и графами.

Матрицы бинарных отношений состоят только из нулей и единиц (см. Лекцию № 5), поэтому можно принять каждый элемент такой матрицы за логическую переменную, принимающую значение 0 или 1, и применить булевы операции над ними, задаваемые таблицами, показанными на рис. 8.1 и рис. 8.5.

	НЕ				И				ИЛИ
a			a	b			a	b
0	1		0	0	0		0	0	0
1	0		0	1	0		0	1	1
			1	0	0		1	0	1
			1	1	1		1	1	1

Рисунок 8.1 – Таблицы истинности булевых функций

НЕ, И, ИЛИ

Пусть матрицы отношений R₁ и R₂ обозначены A и B соответственно.

– Объединение.

Обозначим матрицу результата объединения матриц А и В символом С

.

Символ объединения мы заменили символом логического сложения, так как элементы матрицы С определяются по выражению

,

в соответствии с которым , когда хотя бы одно из слагаемых или оба они равны 1. Значит равносильно тому, что выполняется отношение .

Пример 1. Пусть отношения R₁ и R₂ определяются матрицами А и В, приведенными ниже, тогда отношение будет определяться матрицей С

В терминах теории графов объединение определяется так.

Рисуем три множества вершин и изображаем на одном множестве вершин отношение R₁ штрихпунктирными стрелками (дугами), на втором множестве вершин отношение R₂ штриховыми дугами, вершины третьего множества соединяем сплошными дугами, если между ними на предыдущих рисунках были дуги хотя бы одного типа (см. рис. 8.2, где а и б – графы отношений R₁ и R₂, в – граф результата).

Рисунок 8.2 – Графы отношений R₁ и R₂ и их объединения

– Пересечение.

Пересечение двух отношений в матричной форме определяется как

С = ,

а значения элементов матрицы С определяются по выражению

,

которое равно 1 в том и только в том случае, когда и и , т.е. когда выполнены оба отношения и , а, следовательно, выполнено отношение .

Для матриц А и В примера 1 получаем

В терминах теории графов граф результата получается соединением сплошными дугами только тех вершин, которые соединены дугами одинакового направления и в графе отношения R₁ и в графе отношения R₂ (см. рис. 8.3, где а и б – графы отношений R₁ и R₂, в – граф результата).

– Дополнение.

Отношение – дополнение отношения R₁ до полного отношения определяется путем инвертирования значений элементов исходной матрицы (т.е. заменой нулей единицами, единиц нулями).

Рисунок 8.3 – Графы отношений R₁ и R₂ и их пересечения

Для матрицы А получим такую матрицу дополнения

граф отношения , дополнение графа R₁ (рис. 8.4,а) до полного графа, показан на рис. 8.4,б.

Замечание. В теории графов принято – если в исходном графе нет ни одной петли, то и у графа дополнения петель нет. Здесь же – если в исходном графе петель не было, то у дополнения они будут обязательно (заменяем 0 на 1 на главной диагонали матрицы).

– Разность.

Для определения разности отношений, представленных в матричной форме, воспользуемся представлением разности множеств через дополнение и пересечение (см. п.1.2)

R₁\R₂ = .

Рисунок 8.4 – Графы отношений R₁ и

Данное соотношение определяет алгоритм получения матрицы разности:

– определить дополнение ,

– найти пересечение .

Для матриц примера 1 находим

Для элементов матрицы результата С можно записать

,

что соответствует логической функции запрет (таблица истинности этой функции приведена на рис. 8.5).

		ЗАПРЕТ				М2
a	b			a	b
0	0	0		0	0	0
0	1	0		0	1	1
1	0	1		1	0	1
1	1	0		1	1	0

Рисунок 8.5 – Таблицы истинности булевых функций

ЗАПРЕТ и М2

Граф разности отношений R₁\R₂ получается исключением из графа отношения R₁ дуг, совпавших с дугами графа отношения R₂.

Для графов примера 1 получаем (см. рис. 8.6, где а и б – графы отношений R₁ и R₂, в – граф результата R₁\R₂).

Рисунок 8.6 – Графы отношений R₁ и R₂ и их разности R₁\R₂

– Симметрическая разность.

Матрица результата симметрической разности двух отношений получается поэлементным сложением по модулю 2 матриц отношений, участвующих в операции. Таблица истинности операции сложение по модулю 2 (М2) – ИСКЛЮЧАЮЩЕЕ ИЛИ приведена на рис. 8.5.

Элементы матрицы результата С получаются по формуле

.

Граф результата (рис. 8.7,в) получается объединением не совпадающих частей графов отношений R₁ и R₂, участвующих в операции (из объединенного графа исключается общая часть – результат пересечения графов).

Рисунок 8.7 – Графы отношений R₁ и R₂

и их симметрической разности

– Обратное отношение.

Матрица отношения , обратного к отношению R₁, получается транспонированием матрицы отношения R₁, т.е.

С = А^Т.

При транспонировании происходит поворот матрицы относительно главной диагонали, при котором строки и столбцы матрицы меняются местами.

В графе результата этой операции (рис. 8.8,б) дуги меняют направление по сравнению с исходным графом (рис. 8.8,а).

Рисунок 8.8 – Графы отношений R₁ и

– Составное отношение (композиция).

Для нахождения матрицы составного отношения необходимо перемножить по стандартным правилам матрицы отношений, участвующих в операции, но с учетом того, что умножение и сложение здесь булевские.

Элементы матрицы результата определяются по формуле

,

где n = |M| – число элементов в множестве М.

Граф составного отношения получается следующим образом.

Сначала для графа результата делаем заготовку в виде вершин. Затем находим в графе отношения R₁ (рис. 8.9,а) дугу (если она есть), выходящую из вершины i и входящую в вершину j. После этого просматриваем граф отношения R₂ (рис. 8.9,б) и находим в нем дугу (если она есть), выходящую из вершины j. Пусть эта дуга соединяет вершину j с вершиной k, тогда соединяем в графе результата (рис. 8.9,в) вершины i и k дугой, выходящей из i и входящей в k. таким образом, мы заменяем составной путь i – j – k дугой i – k. Повторяем эту процедуру, пока это возможно.

Граф составного отношения приведен на рис. 8.9,в.

Рисунок 8.9 – Графы отношений R₁ и R₂ и их композиции R_l○R₂

– транзитивное замыкание.

прямое транзитивное замыкание.

Для нахождения прямого транзитивного замыкания в матричном виде наиболее удобна вторая форма его определения

R° = (определение II).

В соответствии с этим определением необходимо получить степени матрицы отношения R и выполнить их объединение. Наивысший порядок степени матрицы отношения R определяется здесь длиной максимального кратчайшего маршрута или цикла в графе, построенном по матрице отношения R. Правда, определять этот граф и маршрут не обязательно, так как после достижения указанной степени результаты возведения в степень начнут повторяться (это может служить признаком окончания процесса получения степеней матрицы отношения R).

Возведение в степень производится по правилам

А² = А·А, А³ = А²·А, А⁴ = А³·А и т.д.

Например, для отношения R₁, представленного матрицей A, получаем

Возведение в степень прекращаем, так как результат будет повторяться.

Таким образом, для прямого транзитивного замыкания отношения R₁ получаем

Для отношения R₂ получаем

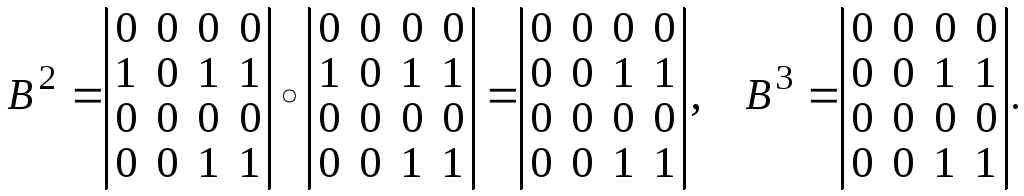
Возведение в степень прекращаем, так как результат повторяется.

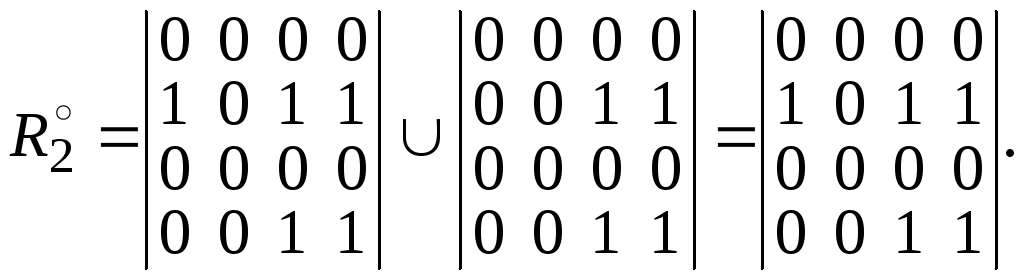
Заметим, для R₁ транзитивное замыкание является полным отношением

, где M = {1, 2, 3, 4}.

Для R₂ транзитивным замыканием является оно само, т.е. .

Для отношения, представленного графом, k–я степень определяется следующим образом.

Если в графе отношения есть путь длины k (путь – это связная последовательность дуг одного направления), начинающийся в вершине i и заканчивающийся в вершине j, то в графе результата эти вершины соединяются дугой, для которой вершина i является началом, а вершина j концом.

Для получения транзитивного замыкания отношения, представленного графом, необходимо объединить графы различных степеней отношения по правилам, приведенным выше.

Граф транзитивного замыкания отношения R₁ (полный граф) приведен на рис. 8.10, а граф транзитивного замыкания отношения R₂ совпадает с графом этого отношения.

Для получения матрицы обратного транзитивного замыкания R^–о необходимо получить степени матрицы обратного отношения R^–1 и выполнить их объединение. (здесь все повторяется, как для матрицы прямого транзитивного замыкания, только с матрицей обратного отношения.)

Для отношения R₁ нашего примера получаем

Р исунок 8.10 – Граф транзитивного и рефлексивного

замыкания отношения R₁

Для получили полное отношение.

Для получаем

Возведение в степень прекращаем, так как результат повторяется.

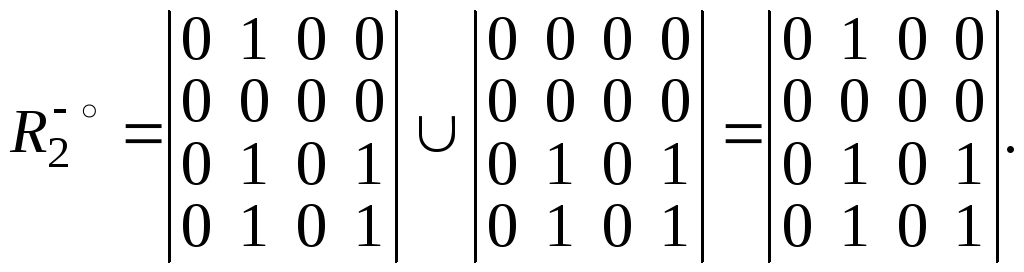Здесь .

Замечание. Если в операциях участвуют отношения на множествах, одно из которых является подмножеством другого (размерности у них разные), то предварительно производится выравнивание размерностей добавлением нулевых строк и столбцов.

– Рефлексивное замыкание.

Прямое и обратное рефлексивные замыкания определяются по формулам

R* = R° E,

R^–* = R^–° E,

где Е – тождественное (оно же диагональное) отношение, в матрице которого 1 стоят только на главной диагонали, а R° и R^–° прямое и обратное транзитивные замыкания отношения R.

Следовательно, для отношений R₁ и R₂ получим

Как видим, для отношения R₁ рефлексивное замыкание является полным отношением, следовательно, его граф будет полным графом, показанным на рис. 8.10.

Для отношения R₂ матрицы как прямого, так и обратного рефлексивного замыкания отличаются от матриц отношений R₂ и только единицами на главной диагонали в строках 1, 2 и 3, поэтому их графы будут отличаться от графов отношений R₂ и только наличием петель при вершинах 1, 2 и 3.

– Редукция.

Применим операцию редукции к отношению R “быть меньше” на множестве М = {1,2,3,4}, которое является строгим порядком.

На рис. 8.11 показаны графы отношения R и его редукции R^r.

Рисунок 8.11 – Графы отношения R и его редукции R^r

Как видим, граф редукции значительно проще графа отношения и в то же время он несет всю информацию об отношении R.

Чтобы перейти от R^r к R, надо выделить в R^r все пути между вершинами и замкнуть их дугами.

Пример 2. Пусть R — отношение на N: R = {(а, b): а > b} — "быть больше".

Выполнить операции над R.

R^–1 = {(a, b): a<b} – "быть меньше";

= U \ R = {(a, b)\ a b} = – "быть не больше",

где Е – тождественное отношение, Е = {(а, b): а = b};

R○R = R² = {(a, b): a – 1 > b} – "быть больше по крайней мере на 2";

R° = R (так как R транзитивно).

Вопросы для контроля

1. Какие булевские операции применяются при выполнении операций над отношениями?

2. Как выполняется операция объединение отношений, представленных матрицами и графами?

3. Как выполняется операция пересечение отношений, представленных матрицами и графами?

4. Как определяются матрица и граф дополнительного отношения по матрице и графу отношения?

5. Как выполняется операция разность отношений, представленных матрицами и графами?

6. Как выполняется операция Симметрическая разность отношений, представленных матрицами и графами?

7. Как определяются матрица и граф обратного отношения по матрице и графу прямого отношения?

8. Как определяется матрица и граф композиции отношений по матрицам и графам операндов?

9. Как выполняются операции прямого и обратного транзитивного замыкания отношений, представленных матрицами и графами?

10. Как выполняется операция рефлексивного замыкания отношений, представленных матрицами и графами?

11. Как выполняется операция Редукция отношения, представленного матрицей и графом?

1 Лекция читается после изучения булевой алгебры и теории графов в качестве демонстрации взаимного проникновения разделов курса.