
1 - Множества / Лекция 4 Операция, функционал, оператор
.doc
5 Лекции № 4. Операция, функционал, оператор.
Отображения, преобразования и перестановки
Продолжительность: 2 часа (90 мин.)
5.1 Ключевые вопросы
5 Лекции № 4. Операция, функционал, оператор. 1
Отображения, преобразования и перестановки 1
5.1 Ключевые вопросы 1
5.2 Текст лекции 1
5.2.1 Операция 1
5.2.2 Функционал и оператор 2
5.2.3 Отображения, преобразования и перестановки 2
5.2.4 Вопросы для контроля 6
5.2 Текст лекции
С понятием функции связаны еще три понятия – операция, функционал и оператор.
5.2.1 Операция
Операция – это функция, у которой значения аргументов и ее собственные значения принадлежат одному и тому же множеству.
Вопрос 1: Можно ли назвать функцию f1 = a – b, у которой аргументы определены на множестве N, операцией?
Ответ: Нет! (Значение функции может оказаться отрицательным, а отрицательные числа не принадлежат множеству N!)
Вопрос 2: Можно ли назвать функцию f2 = a + b, у которой аргументы определены на множестве N, операцией?
Ответ: Да! (Сумма натуральных чисел всегда натуральное число! Следовательно, значения аргументов и функции принадлежат одному множеству N, а потому f2 – операция!)
Поскольку операции это функции, то для их задания применимы все способы задания функций.
Операции обладают следующими свойствами:
Операция * идемпотентна, если x * x = x для любого x М.
Операция * коммутативна, если x * y = y * x для любых x, y М.
Операция * некоммутативна, если x * y y * x для любых x, y М.
Операция * ассоциативна, если x * (y * z) = (x * y) * z для любых x, y, z М.
Операция * дистрибутивна относительно операции °, если
x ° (y * z) = (x ° y) * (x ° z) для любых x, y, z М.
Операции * и ° называют взаимно обратными, если x * y = z тогда и только тогда, когда z ° y = x для любых x, y, z М.
Про операцию * говорят, что она имеет нейтральный элемент, если во множестве М существует элемент (обозначим его e), такой что x * e = x для любого x М.
Если рассматриваемая операция обозначается
знаком +, то нейтральный элемент обычно
называют нулём, если знаком
![]() (умножить), то – единицей.
(умножить), то – единицей.
Про операцию * с нейтральным элементом e говорят, что для неё элемент x М имеет обратный элемент, если для него во множестве М можно найти элемент (обозначим его x') такой, что x * x' = e. Если для всех элементов существуют обратные элементы, то операцию называют обратимой.
5.2.2 Функционал и оператор
Функционал устанавливает связь между множеством функций и множеством чисел. Пример – определенный интеграл
![]() ,
,
где f(x) – функция, a и b – пределы интегрирования, I – число.
Другой пример функционала – наибольшее значение функции f(x) на интервале [a, b].
Оператор определяет еще одну разновидность связи между функциями (ранее были рассмотрены понятия обратной функции и композиции функций). Пример – оператор дифференцирования
Dx = df(x)/dx.
Например, пусть f(x) = sin(x), тогда df(x)/dx = cos(x).
5.2.3 Отображения, преобразования и перестановки
Отображением множества А в множество В называется всюду определенное соответствие g: А→В, т.е. соответствие, у которого Пр1G = A.
Отображением А на В называется всюду определенное и при этом сюръективное соответствие g: А→В, т.е. соответствие, у которого Пр1G = A и Пр2G = B.
отображение
множества A в B
или A на B
обозначают так
![]() .
.
Отображение типа А → А называют преобразованием множества А.
Функция типа А→А, являющаяся отображением А на А, называется перестановкой на А.
Отображение
может быть и неоднозначным. Тогда
совокупность элементов b
для одного a
обозначается как Ga![]() .
Множество Ga – это
образ элемента a
в множестве B.
Элемент a называется
прообразом множества Ga.
.
Множество Ga – это
образ элемента a
в множестве B.
Элемент a называется
прообразом множества Ga.
Пусть
имеется отображение G:
А→В, где для любого a![]() образом является Ga
образом является Ga![]() ,
и пусть имеется множество A1
,
и пусть имеется множество A1![]() .
Совокупность всех
.
Совокупность всех
![]() ,
являющихся образами всех a
,
являющихся образами всех a![]() ,
называется образом множества A1
и обозначается
,
называется образом множества A1
и обозначается
GA1
=![]() .
.
Если A1 и A2 подмножества A, то образ объединения этих подмножеств равен объединению их образов в любом однозначном или неоднозначном отображении
![]() .
.
Действительно
![]()
Однако соотношение
![]()
(образ пересечения подмножеств равен пересечению их образов) справедливо только при однозначном отображении.
Пусть
![]() ,
,
где
![]() – область неоднозначности.
– область неоднозначности.
![]()
Если
![]() (область неоднозначности пуста), то
(область неоднозначности пуста), то
![]() .
.
Довольно
часто рассматриваются отображения на
одном множестве
![]() ,
которые представляются парой (A,
G), где G
= A x
A = A2.
,
которые представляются парой (A,
G), где G
= A x
A = A2.
Пусть G и D отображения A в A.
Композиция этих отображений будет G(D). Если D = G, то G(G) = G2, G2(G) = G3 и т.д.
Если принять G0 = a, то это правило можно распространить и на отрицательные степени
G0 = G (G–1) = G G–1 = a.
Это означает, что G–1 является обратным отображением.
Продолжая, находим
G–1(G–1) = G–2 и т.д.
Для отображений множеств определены прямое и обратное транзитивные замыкания – многократное отображение G или G –1 множества A самого на себя.
Прямое транзитивное замыкание определяется по выражению
![]() для всех
для всех
![]() .
.
Обратное транзитивное замыкание определяется по выражению
![]() для всех
для всех
![]() .
.
Пример 1. Является ли функция f(x) = 2x, имеющая тип N→N, отображением, и если – да, то каким? Имеет ли функция f обратную функцию f –1, и если – да, то является ли f –1 отображением?
Функция
f(x)
= 2x, f:
N→N,
всюду определена на N,
однако не сюръективна, так как область
значений функции f
равна пр2f
= М2п
![]() N (область значений содержит не все
натуральные числа из N,
а только четные). Поэтому f
является отображением N в N или
преобразованием множества N.
N (область значений содержит не все
натуральные числа из N,
а только четные). Поэтому f
является отображением N в N или
преобразованием множества N.
Между
областью определения пр1f
= N и областью
значений пр2f
= М2п
имеет место взаимно однозначное
соответствие: любому элементу п из
N соответствует один и только один
элемент 2n из М2п
и наоборот. Поэтому функция f(х)
= 2х типа f:N→N
имеет обратную функцию f
–1. Однако обратная
функция f –1:
N→N
не всюду определена: ее областью
определения является множество четных
чисел М2п
![]() N. Поэтому обратная функция f
–1 в отличие от исходной
f не является
отображением.
N. Поэтому обратная функция f
–1 в отличие от исходной
f не является
отображением.
Пример 2. Задать несколько возможных типов для функции f(х) = 2n.
Для каждого типа определить:
– свойства функции f;
– является ли f отображением и, если является, то каким?
-
Пусть тип функции f:N→N. Тогда f(х) = 2n всюду определена, так как пр1f = N, но не сюръективна, поскольку пр2f =

 N
(
N
(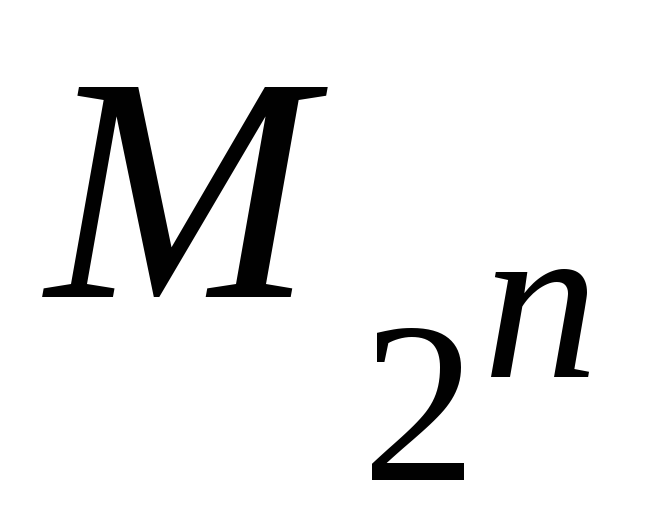 – множество натуральных чисел,
являющихся степенями двойки).
Следовательно, функция f
является отображением N в
N.
– множество натуральных чисел,
являющихся степенями двойки).
Следовательно, функция f
является отображением N в
N. -
f:N→
 .
Тогда функция f
всюду определена и сюръективна,
следовательно, является отображением
N нa
.
Тогда функция f
всюду определена и сюръективна,
следовательно, является отображением
N нa
 .
. -
f: N→R. Функция f всюду определена, но не сюръективна, т.е. f есть отображение N в R.
-
f: R→N. Функция f частично определена и сюръективна, поскольку область значений f(x) = 2n при заданном типе функции f представляет множество натуральных чисел, т.е. пр2f = N, значит не для всех х
 R+
функция f определена,
т.е. пр1f
R+
функция f определена,
т.е. пр1f R+.
Следовательно, f:
R+ →N не является
отображением.
R+.
Следовательно, f:
R+ →N не является
отображением. -
f: R→R. Функция f всюду определена, но не сюръективна (f не имеет отрицательных значений), следовательно, f – отображение R в R.
-
f: R→R+ . Функция всюду определена и сюръективна, т.е. является отображением R на R+.
Кроме названных свойств во всех случаях f есть функциональное соответствие, а для случаев 2 и 6 – взаимно однозначное.
Пример 3. Взаимосвязь между элементами множества двоичных наборов А = {00, 01, 10, 11} и множества В = {0, 1} задано табл. 5.1.
Определить свойства прямого и обратного соответствий, заданных табл. 5.1.
Таблица 5.1
|
a1 |
a2 |
f |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Прямое соответствие (рис. 5.1,а)

Рисунок 5.1 – Графическое представление соответствий,
заданных табл. 5.1
– полностью определено (используются все элементы – наборы множества А),
– сюръективно (все элементы множества В участвуют в соответствии),
– функционально, так как однозначно,
– является однозначным отображением А на В, так как оно полностью определено и сюръективно.
Обратное соответствие (рис. 5.1,б)
– полностью определено,
– сюръективно,
– не однозначно, следовательно, не функционально,
– является неоднозначным отображением В на А по причинам, изложенным выше.
Пример 4. Дано множество А = {a, b, c, d} и два преобразования этого множества (т.е. функции типа А →А, являющихся отображением А в А):
α = (1 → 3, 2 → 3, 3 → 1, 4 → 2); β = (1 → 2, 2 → 1, 3 → 1, 4 → 3).
Эти записи читаются просто: для преобразования α первый элемент заменить третьим, второй элемент заменить третьим, третий элемент заменить первым и т. д. Записывают это обычно так:
![]() ;
;
![]() .
.
Чему равна композиция преобразований?
Композиция преобразований – это новое преобразование:
 ;
;
 .
.
Преобразование
![]() получено так
получено так
 =
(1 → 3 →1, 2 →3 → 1, 3 → 1 → 2, 4 → 2 → 1)
=
(1 → 3 →1, 2 →3 → 1, 3 → 1 → 2, 4 → 2 → 1)
(из
1 по преобразованию α получаем 3, затем
из 3 по преобразованию
![]() получаем 1;
получаем 1;
из 2 по преобразованию α получаем 3, затем …).
Задание:
Композицию
![]() получите самостоятельно.
получите самостоятельно.
Пример 5. Пусть X множество людей.
Для
каждого человека
![]() обозначим Gx множество
его детей. Тогда G2x
– его внуки, G3x
– его правнуки, G–1x
– его родители, G–2x
– дедушка и бабушка и т.д. Изобразив
людей точками, а отображения стрелками,
получим родословную человека.
обозначим Gx множество
его детей. Тогда G2x
– его внуки, G3x
– его правнуки, G–1x
– его родители, G–2x
– дедушка и бабушка и т.д. Изобразив
людей точками, а отображения стрелками,
получим родословную человека.
Если применить операцию прямого транзитивного замыкания для данного примера, то получим прямых потомков человека x.
Для получения всех предков человека следует применить обратное транзитивное замыкание.
5.2.4 Вопросы для контроля
-
Операция – что это такое?
-
Какими свойствами может обладать операция?
-
Поясните понятие функционала.
-
Поясните понятие оператора.
-
Чем различаются отображения множества А в множество В и множества А на множество В?
-
Что такое преобразование множества?
-
Что такое перестановка на множестве?
-
Каковы свойства образов подмножеств множества А?
-
Что такое обратное отображение множества и когда оно существует?
-
Поясните понятия прямого и обратного транзитивных замыканий отображений. Как они определяются?
