3 Лекция № 2. Законы и тождества алгебры множеств

Продолжительность: 2 часа (90 мин.)

3.1 Ключевые вопросы

3 Лекция № 2. законы и тождества алгебры множеств 1

3.1 Ключевые вопросы 1

3.2.1 Основные законы и тождества алгебры множеств 1

3.2.2 Доказательства тождественности формул 3

3.2.3 Семейства множеств 6

3.2.4 Вопросы для контроля 8

3.2.1 Основные законы и тождества алгебры множеств

Основные законы алгебры множеств (булевой алгебры множеств) представляются в виде тождеств, в которых участвуют символы обозначений множеств, включая символы универсального и пустого множеств, и символы операций объединения, пересечения и дополнения.

Ассоциативный закон

1) (XY)Z = X(YZ) = XYZ;

2) (XY)Z = X(YZ) = XYZ.

Коммутативный закон

3) XY = YX; 4) XY = YX.

Закон идемпотентности (повторения)

5) XX = X; 6) XX = X.

Дистрибутивный закон

7. (XY) Z = (X Z) ( Y Z);

8. (XY) Z = (XZ) (YZ) (нет в обычной алгебре).

Законы универсального U и пустого множеств

(законы нуля и единицы 0, U 1)

9) X = X; 10) X = ;

11) XU = U; 12) XU = X;

13) = U; 14) = .

Законы исключенного третьего и противоречия

15) X = U; 16) X = .

Законы де Моргана

17) 18) .

Закон двойного отрицания

19) = X.

Если имеет место включение (множество А является подмножеством множества В, см. рис. 1.1), то

и ,

и .

Законы 5) и 6) можно записать и так

XXXX … = X, XXXX… = X,

что позволяет при выполнении операций объединения и пересечения обходиться без коэффициентов и показателей степеней.

При работе с множествами могут оказаться полезными тождества, приведенные ниже. Однако они требуют доказательства. Доказать их можно, используя основные законы (свойства операций пересечения, объединения и дополнения) и приемы, рассмотренные в п. 3.2.3

Дистрибутивный закон пересечения относительно разности

.

Дистрибутивный закон пересечения относительно симметрической разности

.

Дистрибутивный закон разности относительно пересечения

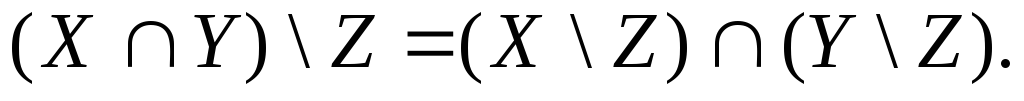
Дистрибутивный закон разности относительно объединения

.

Дистрибутивные законы объединения и пересечения относительно разности

X\(YZ) = (X\Y) (X\Z);

X\(YZ) = (X\Y) (X\Z).

Представление пересечения и объединения через разность

XZ = X\(X\Z);

XY= (X\Y) (Y\X) (XY) = (X\Y) (Y\X) X\(X\Y).

Законы нуля и единицы для разности

(X \Y) (XY) = ; X \ = X \U = ;

\X =; U\X =; X \X = U.

Законы поглощения

Закон склеивания

.

Свойства симметрической разности

,

,

,

,

,

.

3.2.2 Доказательства тождественности формул

Наиболее часто в теории множеств возникает необходимость доказательства равенства соотношений типа Х = Y.

Доказательство можно проводить путем рассуждений с применением законов и тождеств алгебры множеств, построением диаграмм Эйлера–Венна или на примерах конкретных множеств, составленных, например, из алфавитно–цифровых символов (последние два способа приведены в примере 2 п. 2.2.5 Лекции №1).

Ниже, в примерах, доказательства соотношений типа X = Y, где Х и Y – множества, основаны на использовании определений I и II равенства двух множеств.

В соответствии с определением I для равенства двух множеств требуется совпадение их элементов. Поэтому сначала доказывается, что для произвольного элемента а из того, что , следует, что , затем доказывается, что если , то . Таким образом, элементы множеств X и Y совпадают и, следовательно, по определению I Х = Y.

В соответствии с определением II Х = Y, если и . Поэтому для доказательства равенства двух множеств требуется показать справедливость включений и .

Пример 1. Доказать справедливость соотношения

.

Предположим, что произвольный элемент , т.е. что . Это значит, что и , значит и .

Следовательно, .

Пусть теперь некоторый элемент , т.е. и . Это значит, что и , т.е. .

Следовательно, .

Таким образом, доказано, что .

Пример 2. Докажем по другому справедливость соотношения

.

Пусть имеем

U ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {0, 1, 3, 7}, B = {2, 3, 4, 6, 7}.

Определим левую часть:

= {0, 1, 3, 7}{2, 3, 4, 6, 7} = {0, 1, 2, 3, 4, 6, 7},

= U\() =

= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}\{0, 1, 2, 3, 4, 6, 7} = {5, 8, 9}.

Определим правую часть:

= U\A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}\{0, 1, 3, 7} = {2, 4, 5, 6, 8, 9},

= U\B ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}\{2, 3, 4, 6, 7} = {0, 1, 5, 8, 9},

= {2, 4, 5, 6, 8, 9}{0, 1, 5, 8, 9} = {5, 8, 9}.

Как видим, левая часть равна правой, следовательно, соотношение справедливо.

Замечание. Результаты операций при доказательстве тождеств не должны быть равными .

Пример 3. Доказать справедливость соотношения

(A\B)\C = A\(BC).

Используем соотношение .

Левая часть

(A\B)\C = \С = .

Правая часть

A\(BC) =

Как видим, левая часть равна правой, следовательно, соотношение справедливо.

Пример 4. Доказать справедливость соотношения

.

Это свойство дистрибутивности слева объединения относительно пересечения .

Такое доказательство может быть выполнено с помощью диаграмм Эйлера–Венна (см. пример 2, п. 1.3). Здесь для этих целей используем один из приемов доказательства равенства двух множеств.

В соответствии с первым определением равенства множеств множества равны, если их элементы совпадают. Это означает, что Х = Y, если из того, что , следует , и из того, что , следует .

1. Покажем сначала, что если произвольный элемент а принадлежит левой части соотношения, т.е. , то он принадлежит и правой части данного соотношения, т.е. .

Пусть .

Из определения операции объединения следует, что элемент а принадлежит объединению множеств А и , если он принадлежит хотя бы одному из них (или, что очевидно, тому и другому). Таким образом, или , при этом возможны следующие случаи:

1.1. а принадлежит множеству А и а не принадлежит пересечению множеств :

и .

Последнее условие выполняется, если а не принадлежит В, или С, или им обоим (это является лишним);

1.2. и , т.е. ;

1.3. и , т.е. .

Рассмотрим каждый из этих случаев.

1.1. Так как , то а принадлежит объединению множества А с любым множеством, в том числе и . Следовательно, а принадлежит и их пересечению:

.

1.2. Так как , , то и , следовательно, .

1.3. Так как , то этого достаточно, чтобы и , следовательно, .

Таким образом, в любом из рассмотренных случаев из того, что , следует, что .

2. Покажем теперь справедливость второго условия определения I равенства множеств: если произвольный элемент а не принадлежит левой части соотношения , то он не принадлежит и правой части данного соотношения .

Пусть теперь: .

Элемент а не принадлежит объединению двух множеств, если он не принадлежит ни одному их них. Тогда А и , т.е. возможны следующие случаи:

2.1. ;

2.2. ;

2.3. .

Рассмотрим каждый из этих случаев:

2.1. Так как , то , следовательно,

.

2.2. Так как , то , следовательно,

.

2.3. Так как , то этого достаточно, чтобы , следовательно, .

Как видим, в любом из этих случаев из того, что , следует, что .

Таким образом, множества и совпадают и по определению равенства множеств

,

что и требовалось доказать.

Пример 5. Доказать справедливость соотношения

.

Это свойство дистрибутивности справа пересечения относительно объединения .

Введем символ , который в выражениях типа РQ будет означать: "если справедливо Р, то справедливо и Q" или "из того, что Р, следует Q".

Множества Х = Y, если и .

1. Поэтому покажем сначала, что , т.е. любой произвольный элемент а из множества, заданного левой частью соотношения, принадлежит и множеству, заданному правой частью соотношения.

Пусть . Тогда

и

( или ) и ()

( и ) или ( и )

или

.

Таким образом, .

2. Покажем теперь, что , т.е. любой элемент а из множества, заданного правой частью исходного соотношения, принадлежит и множеству, заданному левой частью исходного соотношения.

Пусть . Тогда

или

( и ) или ( и )

( или ) и

( и

Следовательно, .

Таким образом, ,

что и требовалось доказать.