2.2.4 Операции над множествами

Объединением множествА и В (обозначается) называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множествA,B(рис. 2.2):

= {x:или}.

Пересечением множествAиВ (обозначается) называется множество, состоящее из всех тех и только тех элементов, которые принадлежат иА, иВ (рис. 2.3):

= {x:и}.

Если общих элементов в множествах AиBнет, то=

Пусть U–универсальное множество такое, что все рассматриваемые множества являются его подмножествами.

Дополнением (доU) множестваА (обозначается) называется множество всех элементов, не принадлежащихA, но принадлежащихU (рис. 2.4):

= U \ A.

Операции объединения, пересечения и дополнения {} часто называютбулевыми операциями над множествами, а алгебру множеств, в которой используются только эти операции, – булевой алгеброй множеств.

Рисунок 2.2 – Диаграмма объединения множеств АиВ

Рисунок 2.3 – Диаграмма пересечения множеств АиВ

Рисунок 2.4 – Диаграмма дополнения множества А

В алгебре множеств, кроме рассмотренных операций, определены также операции разности, симметрической разности и прямого (декартова) произведения множеств.

Разностью множествА иВ (обозначаетсяА\В) называется множество всех тех и только тех элементовА, которые не содержатся вВ (рис. 2.5):

А\В= {x:и}.

Разность множеств – операция строго двуместная и некоммутативная: в общем случае

А\В В\А.

Разность множеств можно представить через пересечение и дополнение

A\B = .

Рисунок 2.5 – Диаграмма разности множеств А и В

Симметрической разностью множествА иВ (обозначаетсяАB) называется множество всех тех элементовА или B, которые не содержатся вAиВ одновременно (рис. 2.6):

АВ= {x:или, но}.

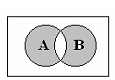
Рисунок 2.6 – Диаграмма симметрической разности множеств АиВ

Прямое (декартово) произведение множеств Aи B – это множество элементов в виде упорядоченных пар (a,b), где

Для этой операции можно записать

{()|}.

Элементы () называются кортежами (векторами, наборами, словами). В произведении могут участвовать более двух множеств. Количество множеств, участвующих в произведении, определяет длину кортежей.

Произведение множеств – операция некоммутативная

,

поэтому элементы кортежей нельзя переставлять.

В множествах АиВмогут быть одинаковые элементы, поэтому и в кортеже могут оказаться одинаковые элементы, например как буквы в словах.

Если множество А умножается на себя, то можно записать

,и т.д.

где А², А³ – степени множества А.

Произведение двух множеств A= {a₁,a₂,a₃} иB= {b₁,b₂} можно представить в виде графика, показанного на рис. 2.7, где каждая вертикальная линия обозначена элементом изА, каждая горизонтальная линия элементом изВ, а каждая жирная точка представляет пару (a_i,b_i).

Рисунок 2.7 – График произведения множеств А и В

Пример 1. Пусть универсальное множествоU – множество всех сотрудников некоторой фирмы;А – множество всех сотрудников данной организации старше 35 лет;В – множество сотрудников, имеющих стаж работы более 10 лет; С – множество менеджеров фирмы. Каков содержательный смысл (характеристическое свойство) каждого из следующих множеств:

а) ; б); в); г)В \ С; д)С\B?

а) – множество сотрудников организации, стаж работы которых не превышает 10 лет.

б) – множество менеджеров фирмы не старше 35 лет, имеющих стаж работы более 10 лет.

в) – множество всех сотрудников фирмы старше 35 лет, а также сотрудников, не менеджеров, стаж работы которых более 10 лет.

г) В\С – множество сотрудников организации со стажем работы более 10 лет, не работающих менеджерами.

д) С\В – множество менеджеров со стажем работы не более 10 лет.

Пример 2. Задать множества,, если:

М – множество всех натуральных чисел, не превосходящих 100;

N – множество натуральных чисел.

– множество всех натуральных чисел, больших 100.

Запись без указания универсального множестваU не ясна:

– то ли это множество всех отрицательных целых чисел;

– то ли это множество положительных дробных чисел;

– то ли это пустое множество натуральных чисел.

Пример 3. Осуществить операции объединения, пересечения, дополнения, разности и симметрической разности над множествами

А = {a, b, c, d} и B = {с, d, e, f, g, h}.

= {a, b, c,d,e, f, g, h};

= {c, d}.

A \ B = {a, b};

B \ A = {e, f, g, h};

{a, b,e, f, g, h}.

Универсальное множество U не определено, поэтому, строго говоря, операции дополнения над множествамиAиВне могут быть выполнены. Если принять в качестве универсального множества объединение множествA и B

U= {а,b,с,d,e,f,g,h}, тогда

=U\А = {е, f, g,h}, = U\B = {а, b}.

Пример 4. ПустьU = {1, 2, 3, 4},А = {1, 3, 4},В = {2, 3}, С ={1, 4}.

Найти:

a) ; б) ; в); г).

a)== ({1, 2, 3, 4} \ {1, 3, 4})({1, 2, 3, 4}\{2, 3}) =

{2}{1, 4} = {1, 2, 4}.

б) = = {1, 2, 3, 4}\ ({1, 3, 4}{2, 3}) = {1, 2, 3, 4}\{3} =

= {1, 2, 4}.

в) =={l, 3, 4}({l, 2, 3, 4}\{2, 3}) ={1, 3, 4}{1, 4} =

= {1, 4}.

г) = ({2, 3}\{1, 3, 4})({1, 2, 3, 4}\{1, 4}) ={2}{2, 3} =

= {2, 3}.

Пример 5. Получить прямое произведение множеств

А = {a, b} и В = {p, q, r}.

АВ = {(a, p),(a, q),(a, r),(b, p),(b, q),(b, r)}.