11

6 Лекция № 5.Отношения

Продолжительность:2 часа (90 мин.)

6.1 Ключевые вопросы

6 Лекция № 5. отношения 1

6.1 Ключевые вопросы 1

6.2 Текст лекции 1

6.2.1 Отношения 1

6.2.2 Операции над отношениями 4

6.2.3 Свойства операций над отношениями 8

6.2.4 Вопросы для контроля 11

6.2 Текст лекции

6.2.1 Отношения

Отношения – один из способов задания взаимосвязей между элементами множеств. Чаще всего используются унарные и бинарные отношения.

Унарные (одноместные) отношения отражают наличие какого–то определенного признакаR (свойства и т.п.) у элементов множестваМ (например, "быть четным" на множестве натуральных чисел). Тогда все такие элементыа из множестваМ, которые отличаются данным признакомR, образуют некоторое подмножество вМ, называемое унарным отношениемR, т.е. и.

Бинарные (двухместные) отношения используются для определения каких–то взаимосвязей между парами элементов множестваМ (так, на множестве людей могут быть заданы, например, следующие бинарные отношения: "жить в одном городе", "быть моложе", "быть сыном", "работать в одной организации" и т.п.). Тогда все пары (а,b) элементов изМ, между которыми имеет место данное отношениеR, образуют подмножество пар из множества всех возможных пар элементов = М ², называемое бинарным отношениемR, т.е., при этом.

В общем случае могут рассматриваться п–местные (n–арные) отношения, например отношения между тройками элементов – трехместные (тернарные) отношения и т.д.

Вот пример тернарного отношения “образовывать сумму”

x+y=z

и отношения для четверок –“находиться в отношении пропорциональности”

x/y=z/v.

Под п–местным отношением понимают подмножествоR прямого произведенияп множеств: .

Говорят, что элементы а₁, а₂, ...,а_n находятся в отношенииR, если

Если n–местное отношениеR задано на множествеМ, т.е.

M₁= M₂ =…= M_n = М, то

Рассмотрим детально бинарные отношения.

Итак, двухместным, или бинарным, отношениемR называется подмножество парпрямого произведения, т.е.. При этом по аналогии с соответствиями множествоМ₁ называют областью отправления отношенияR, множествоМ₂ – областью прибытия. Часто рассматривают отношенияR между парами элементов одного и того же множестваМ, тогда. Еслиа и b находятся в отношенииR, это записывается какаRb.

С отношениями связаны еще два понятия

– область определения D(R) и

– область значений Q(R),

определяемые соответственно

, .

На рис. 6.1 приведен условный пример отношения.

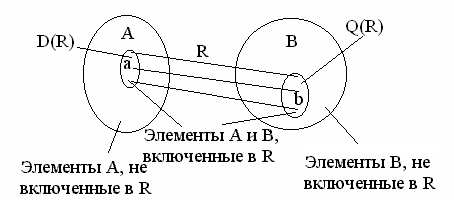
Рисунок 6.1 – Пример отношения R

Для задания бинарных отношений годятся любые способы задания множеств, так как отношения это подмножества некоторых множеств – прямых произведений двух множеств.

Отношения, определенные на конечных множествах, обычно задаются:

– Списком (перечислением) пар, для которых это отношение выполняется. Например,R = {(а, b), (а, с), (b, d)}.

Кроме такого представления, заимствованного у множеств, для отношений применяют также представление в виде матриц и графов.

– Бинарному отношению , гдеM = {а₁, а₂,...,а_п}, соответствуетквадратная матрицапорядкап, в которой элементc_ij, стоящий на пересеченииi–ой строки иj–ого столбца, равен 1, если между элементамиa_iиа_j имеет место отношениеR, или 0, если оно отсутствует:

Если , гдеM₁ = {а₁, а₂,...,а_п},M₂ = {b₁, b₂,...,b_m}, томатрица получается прямоугольнойсnстроками иmстолбцами.

– бинарному отношению, гдеM = {а₁, а₂,...,а_п}, соответствуеториентированный граф(орграф), вершины которого взаимно однозначно соответствуют элементам множестваМ, а дуги соответствуют отношениям между элементами множестваМ. Например, дуга, соединяющая пару элементова_i иа_j в направлении ота_i ка_j, показывает наличие отношенияа_iRа_j.

Если , гдеM₁ = {а₁, а₂,...,а_п},M₂ = {b₁, b₂,...,b_m}, тографполучаетсядвудольный(см. [16]):одна доля – множество вершинM₁, другая доля – множество вершинM₂, а дуги соответствуют отношенияма_iRb_j.

Введем следующие понятия:

Пустое отношение– отношение, которое не выполняется ни для одной пары элементов множестваМ. Обозначается это отношение символом.

Матрица этого отношения содержит только 0, а граф состоит только из вершин (нуль граф).

Полное отношение– отношение, которое выполняется для любой пары элементов множестваМ. Обозначается оноU=.

Матрица этого отношения содержит только 1. В графе этого отношения каждая вершина соединена дугой с каждой вершиной, включая ее самою (полный граф).

Диагональное отношениеE(оно жетождественное отношение, оно жеотношениеравенства) – отношениеaEb, которое выполняется только, еслиa и b это один и тот же элемент.

В матрице этого отношения элементы, расположенные на главной диагонали, равны 1, а остальные элементы равны 0. В графе этого отношения, кроме петель при каждой вершине, других дуг нет.

Пример 1. ПустьМ = {1, 2, 3, 4}.

Задать в явном виде (списком), матрицей и графом отношение , еслиR означает – "быть меньше".

Отношение R как множество содержит все пары элементова,b изМтакие, чтоа < b:

Следовательно, R = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}.

Матрица отношения приведена на рис. 6.2,а.

Граф отношения приведен на рис. 6.2,б.

Рисунок 6.2 – Граф отношения R

Пример 2. ПустьМ = {1, 2, 3, 4}.

Составить матрицы отношений , если:

– R₁ – "быть делителем";

– R₂ – "иметь общий делитель, отличный от единицы";

– R₃– "иметь один и тот же остаток от деления на 3".

1) и выполняется для пар

{(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4, 4)}.

Эти пары определяют наличие единиц в матрице отношенияна пересечении строки элементаа и столбца элементаb(рис. 6.3,а);

2)

Матрица отношения R₂ представлена на рис. 6.3,б;

3) a иbимеют одинаковый остаток от деления на 3}. Матрица отношенияR₃ приведена на рис. 6.3,в.

R1	1	2	3	4			R2	1	2	3	4			R3	1	2	3	4
1	1	1	1	1			1	0	0	0	0			1	1	0	0	1
2	0	1	0	1			2	0	1	0	1			2	0	1	0	0
3	0	0	1	0			3	0	0	1	0			3	0	0	1	0
4	0	0	0	1			4	0	1	0	1			4	1	0	0	1
		а)							б)							в)

Рисунок 6.3 – Матрицы отношений R₁,R₂,R₃Примера 2