2.2.6 Логический анализатор.

Логический анализатор предназначен для отображения на экране монитора 16-разрядных кодовых последовательностей одновременно в 16 точках схемы. На рис. 1.29 представлен внешний вид иконки логического анализатора, а на рис. 1.30 – лицевая панель логического анализатора.

Анализатор снабжён двумя визирными линейками, позволяющими получать точные отсчёты временных интервалов Т1, Т2 и Т2 – Т1, а также линейкой прокрутки по горизонтали.

В блоке Clock имеются клеммы для подключения как обычного (External), так и избирательного (Qualifier) источника запускающих сигналов, параметры

Рис. 1. 29. Внешний вид иконки логического анализатора.

Рис. 1.30. Лицевая панель логического анализатора.

которых задаются с помощью соответствующего диалогового окна, вызыва-емого кнопкой Set.

Запуск логического анализатора можно производить по переднему (Positive) или заднему (Negative) фронту запускающего сигнала с использованием внешнего (External) или внутреннего (Internal) источника. В окне Clock можно установить значение логического сигнала (0, 1 или Х), при котором производится запуск анализатора.

2.2.7 Логический преобразователь.

Логический преобразователь предназначен для выполнения различных функциональных преобразований в схеме.

На рис. 1.31 представлен внешний вид иконки логического преобразователя, а на рис. 1.32 – лицевая панель логического преобразователя.

Рис. 1.31. Внешний вид иконки логического преобразователя.

Рис. 1.32. Лицевая панель логического преобразователя.

С помощью логического преобразователя можно осуществлять следующие операции:

• кнопка - получение таблицы истинности исследуемой схемы;

• кнопка - преобразование таблицы истинности в логическое выражение;

• кнопка - преобразование таблицы истинности в минимизированное логическое выражение;

• кнопка - преобразование логического выражения в таблицу истинности;

• кнопка - создание логических схем по заданному логическому выражению;

• кнопка - синтез логических схем на элементах И-НЕ по заданному логическому выражению.

Контрольные вопросы.

1. Как измерить сопротивление с помощью мультиметра?

2. Какие требования предъявляются к схеме, в которой производится измерение сопротивлений с помощью мультиметра?

3. Чем отличаются выходы функционального генератора?

4. Каким образом в функциональном генераторе можно получить однополярный сигнал?

5. Каким образом с помощью осциллографа можно получить значения амплитуды сигнала и его частоты?

6. Каким образом можно получить разноцветные осциллограммы сигналов на экране осциллографа и как их разнести по вертикали для удобства наблюдения?

7. Какие режимы синхронизации имеет осциллограф и что они определяют?

8. Как можно получить точные значения коэффициента усиления и фазового сдвига на данной частоте с помощью графопостроителя АЧХ и ФЧХ?

9. Каким образом в генераторе слов задаются двоичные комбинации сигналов?

10. Какие операции можно осуществить с помощью логического преобразователя?

Часть 3. Лабораторный практикум.

ЛАБОРАТОРНАЯ РАБОТА №1.

Исследование амплитудного модулятора.

Цель работы:

1. Исследование схемы амплитудного модулятора.

2. Исследование влияния параметров модулирующего сигнала на величину коэффициента модуляции.

1.1 Подготовка к работе.

• Повторить раздел: «Амплитудная модуляция».

• Повторить основные меню и элементную базу программы «Electronics Workbench».

1.2 Краткая теоретическая часть.

Радиосвязь осуществляется путём передачи энергии электромагнитных колебаний высокой частоты от передающей антенны к приёмной. Для осуществления радиосвязи изменяют один из параметров высокочастотного колебания по закону изменения низкочастотного сигнала. Такой процесс называется модуляцией, а устройство, его осуществляющее, называется модулятором.

Амплитудная модуляция. При амплитудной модуляции (АМ) амплитуда высокочастотного колебания изменяется по закону сигнала информации. Модуляция по амплитуде сводится к перемножению модулирующего U и несущего X сигналов.

U = Uo + U1 = Uo + ∆U sinΩt, X = Xm sinωt,

где Uo – амплитуда колебаний при отсутствии модуляции,

U1 = ∆U sinΩt – переменная составляющая модулирующего сигнала,

∆U – изменение амплитуды модулирующего сигнала,

Ω = 2πF – частота модулирующего сигнала,

Xm - амплитуда несущего сигнала,

ω - частота несущего сигнала.

Мгновенное значение амплитуды высокочастотных колебаний можно записать в виде:

U = Uo + ∆U sinΩt = Uo[1 + (UΩ/Uo) sinΩt].

После перемножения и тригонометрических преобразований получим результирующее колебание в следующем виде:

U = Uo{sinωt + 0,5M[cos(Ω - ω)t + cos(Ω + ω)t]},

где Uo = (Umax – Umin)/2M,

M = UΩ/Uo = (Umax – Umin)/ (Umax + Umin) - коэффициент модуляции.

Временная диаграмма радиосигнала с амплитудной модуляцией показана на рис. 1.1.

Рис.1.1. Временная диаграмма радиосигнала с амплитудной модуляцией.

Для примера на рис. 1.2 приведены диаграммы модулирующего гармонического сигнала S(t) и модулированного радиосигнала Z(t) с коэфицентами модуляции m=0,5 (рис. 1.2 б) и m=1 (рис. 1.2 в).

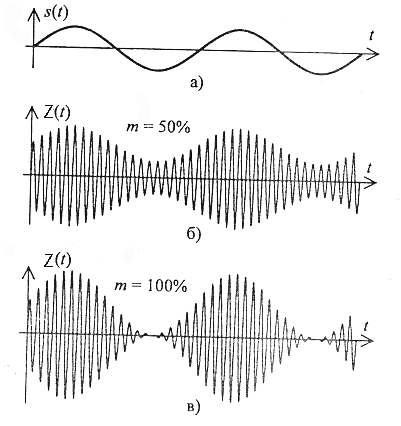
Рис.1.2

Схема амплитудного модулятора показана на рис. 1.3. Она содержит двухвходовой суммирующий усилитель на ОУ, к одному входу которого подключен источник постоянного напряжения Uо, к другому — источник модулирующего напряжения U1 = ∆U sinΩt. Выход усилителя подключён к Х-входу перемножителя с коэффициентом передачи 1. На Y-вход перемножителя подается сигнал несущей X. После перемножения на выходе перемножителя будет сформирован сигнал, показанный на рис. 1.1.

Рис. 1.3 Схема амплитудного модулятора.

Угловая модуляция. Угловая модуляция является общим для частотной и фазовой модуляции. Фазовой называется такая модуляция, при которой приращение фазового угла φ пропорционально приращению ∆Uу модулирующего сигнала. Частотной называется такая модуляция, при которой приращение ∆Uу напряжения модулирующего сигнала вызывает пропорциональное приращение частоты ∆, а это косвенно влияет на изменение фазового угла ∆φ. Оба вида угловой модуляции взаимно связаны. Связь между ними формулируется следующим образом: изменение частоты во времени по закону эквивалентно изменению полной фазы по закону интеграла, а изменение полной фазы по закону эквивалентно изменению частоты по закону производной. Это положение, являющееся основным в теории угловой модуляции, определяет связь между изменениями частоты и фазы и указывает на общность, существующую между двумя разновидностями угловой модуляции — модуляцией частоты (ЧМ) и модуляцией фазы (ФМ).

Сигнал с частотной модуляции в простейшем случае описывается выражением:

Z(t) = Xm sin[ωt + (∆ω/Ω) sinΩt],

где Xm — амплитуда несущей;

∆ω —диапазон частотного отклонения (девиации) несущей под действием модулирующего (в данном случае — синусоидального) сигнала.

Из последнего выражения видно, что периодическая модуляция частоты эквивалентна гармонической вариации фазы с той же частотой, при этом амплитуда получаемой вариации фазы равна Ф = ∆ω/Ω = М.

Это отношение численно равно индексу модуляции М, являющемуся основным параметром угловой модуляции. Индекс модуляции не зависит от средней (немодулированной) частоты ω, a определяется исключительно величиной девиации и модулирующей частотой.

Сигнал с фазовой модуляции описывается выражением:

Z(t) = Xm sin[ωt + Ф sinΩt].

При модуляции гармоническим сигналом по характеру колебания и его свойствам с учётом обозначения Ф = ∆ω/Ω нельзя сделать однозначное заключение о том, с какой модуляцией мы имеем дело — с частотной или фазовой. При частотной модуляции величина девиации ∆ω пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции, однако с ростом последней индекс модуляции уменьшается. При фазовой же модуляции величина Ф пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции.

Для примера на рис. 1.4 приведен график сигнала с ЧМ при гармоническом модулирующем сигнале S(t).

Рис. 1.4