
Домашняя контрольная работа № 4 (7, 8)
6. Найти число ν моль и число N молекул, содержащихся в объеме V =1 см3 воды при температуре t = 4 °C.
Дано:
V =1 см3 = 10-6 м3
t = 4 °C
----------------------
ν -? N -?
Решение:
Количество вещества найдем через массу и молярную массу воды:
 (1),
(1),
где
μ
= 18∙10-3
 – молярная масса воды;
– молярная масса воды;
m – масса воды:
 (2),
(2),
где
ρ
=
103
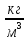 – плотность воды при температуре t
= 4 °C.
– плотность воды при температуре t
= 4 °C.
Подставим (2) в (1):
 (3)
(3)
Число N молекул, содержащихся в объеме V:
 (4),
(4),
где NA = 6,02∙1023 моль-1 – число Авогадро.
Подставляя в (3) и (4) числовые значения величин произведем вычисление:
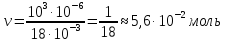

Ответ: ν = 5,6∙10-2 моль; N = 3,37∙1022
17. Два сосуда одинаковой емкости содержат идеальный газ. В одном сосуде давление р1 = 1 МПа и температура Т1 = 400 К, в другом сосуде р2 = 1,5 МПа, Т2 = 250 К. Сосуды соединили трубкой и охладили находящийся в них газ до температуры Т = 300 К. Определить установившееся давление в сосудах.
Дано:
р1 = 1 МПа = 106 Па
Т1 = 400 К
р2 = 1,5 МПа = 1,5∙106 Па
Т2 = 250 К
Т = 300 К
---------------------------------
р -?
Решение:
Согласно уравнению состояния идеального газа (уравнению Менделеева – Клапейрона) для газов в сосудах справедливо соотношения:
 (1)
(1)
 (2)
(2)
Из (1) и (2) выразим количество вещества каждого газа:
 (3)
(3)
 (4)
(4)
Количество вещества смеси газов:
 (5)
(5)
Подставим (3) и (4) в (5):
 (6)
(6)
Согласно уравнению состояния идеального газа (уравнению Менделеева – Клапейрона) для смеси газов:
 (7),
(7),
где в левой части 2∙V – общий объем двух сосудов.
Подставим (6) в (7):

Откуда
выразим давление смеси газов:
 (8)
(8)
Проверка
размерности:

Подставляя в (8) числовые значения величин произведем вычисление:
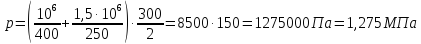
Ответ: р = 1,275 МПа
28. Определить среднюю длину свободного пробега и среднее число столк-новений молекулы гелия при температуре Т = 400 К и давлении р = 1 Па.
Дано:
Т = 400 К
р = 1 Па
-------------------------
р -?
Решение:
Cредняя
длина свободного пробега
 молекул газа:
молекул газа:
 (1),
(1),
где d – диаметр молекул гелия: d = 1,9∙10-10 м
Концентрация
молекул газа найдем из формулы взаимосвязи
давления и тер-модинамической температуры:
 ,
,
где
k
= 1,38∙10-23
 –
постоянная Больцмана.
–
постоянная Больцмана.
Откуда
получим:
 (2)
(2)
Подставим
(2) в (1):
 (3)
(3)
Среднее
число столкновений молекул газа:
 (4)
(4)
Cредняя
арифметическая скорость молекул газа:
 (5),
(5),
где
R
= 8,31
 – молярная газовая постоянная;
– молярная газовая постоянная;
μ
= 4∙10-3
 – молярная масса гелия.
– молярная масса гелия.
Подставим
(5) в (4):
 (6)
(6)
Проверка
размерности:


Подставляя в (3) и (6) числовые значения величин произведем вычисление:


Ответ:
 = 3,43∙10-2
м;
= 3,43∙10-2
м;
 = 4,25∙104
с-1
= 4,25∙104
с-1
35. Определить среднюю кинетическую энергию wвращ вращательного дви-жения одной молекулы двухатомного газа, если суммарная кинетическая энергия молекул одного киломоля этого газа U = 3,01 МДж.
Дано:
U = 3,01 МДж = 3,01∙106 Дж
ν = 1 кмоль = 103 моль
-------------------------------------
wвращ -?
Решение:
Внутренняя
энергия газа всех молекул газа U
и средняя кинетическая энергия молекулы
газа w
связаны соотношением:
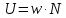 (1),
(1),
где
N
– число молекул газа:
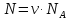 (2),
(2),
где NА – число Авогадро: NА = 6,02∙1023 моль-1
Подставим
(2) в (1):

Откуда
выразим среднюю кинетическую энергию
одной молекулы двухатом-ного газа:
 (3)
(3)
Cредняя
кинетическая энергия w
одной
молекулы газа выражается через число
степеней свободы молекулы:
 (4),
(4),
где i – число степеней свободы, для двухатомного газа:

Приравниваем правые части (3) и (4):
 (5)
(5)
Cредняя кинетическая энергия wвращ вращательного движения одной молекулы двухатомного газа:
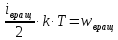 (6)
(6)
Поделим
(6) на (5):

Откуда
выразим
среднюю
кинетическую энергию wвращ
вращательного
движе-ния одной молекулы двухатомного
газа:
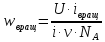 (7)
(7)
Проверка размерности:

Подставляя в (7) числовые значения величин произведем вычисление:

Ответ: wвращ = 2∙10-19 Дж
45. Совершая цикл Карно, газ получил от нагревателя теплоту Q1 = 1 кДж и совершил работу А = 200 Дж. Температура нагревателя Т1 = 375 К. Определить температуру охладителя.
Дано:
Q1 = 1 кДж = 1000 Дж
А = 200 Дж
Т1 = 375 К
----------------------------
Т2 -?
Решение:
КПД цикла выразим через количество теплоты, полученном от нагревателя и работу, совершенную газом:
 (1)
(1)
КПД цикла выразим через температуру нагревателя и охладителя:
 (2)
(2)
Приравниваем правые части (1) и (2):

Откуда выразим температуру охладителя:
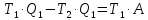
 (3)
(3)
Проверка размерности:

Подставляя в (3) числовые значения величин произведем вычисление:

Ответ: Т2 = 300 К
55. 2 кг воды нагреваются от 10°С до 100 °С и при этой температуре обраща-ются в пар. Определить изменение энтропии в этом процессе.
Дано:
m = 2 кг
t1 = 10 °C; T1 = 283 К
t2 = 100 °C; T2 = 373 К
----------------------------
S -?
Решение:
Изменение энтропии в процессах:
а) нагревание воды от 10°С до 100 °С
 (1),
(1),
где
с
= 4190
 – удельная теплоемкость воды.
– удельная теплоемкость воды.
б) испарение воды при 100 °С
 (2),
(2),
где
r
= 2,26∙106
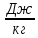 – удельная теплота парообразования
воды.
– удельная теплота парообразования
воды.
Результирующее изменение энтропии равно:
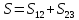 (3)
(3)
Подставляем (1) и (2) в (3):
 (4)
(4)
Проверка размерности:

Подставляем в (4) числовые значения величин и произведем вычисление:

Ответ:
S
= 14,4

