Работа сау

Под действием управляющего и возмущающих воздействий в САУ возникают динамические процессы, т.е. процессы, протекающие во времени. Управляющие воздействия являются детерминированными величинами т.е. их поведение заранее известно.

F(t) – случайные величины, они подчиняются законам математической статистики.

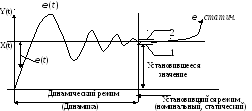
Режим работы, когда Y(t) постоянен и практически не изменяется – это номинальный режим (установившийся режим или статика).

Динамический режим или динамика.

В динамическом режиме происходит изменение во времени регулируемой величины, поэтому динамический режим описывается дифференциальными уравнениями.

На установившемся режиме Y(t)=const, поэтому уравнения статики - алгебраические уравнения.

Для того, чтобы из уравнений динамики получить уравнения статики, надо все производные в дифференциальных уравнениях приравнять к нулю.

По поведению системы на установившемся режиме различаются:

1. Статические системы.

Статические системы – это такие системы, у которых регулируемая величина зависит от нагрузки.

- статизм системы

Особенностью статистических систем является то, что они всегда работают со статической ошибкой. Статическая ошибка является принципом работы статической системы. В статической системе нет интегрирующих элементов.

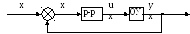
Изменяя характеристики системы, мы можем уменьшить уст., но она никогда не будет равна 0.

(при X(t)=1)

2. Астатические системы.

Это такие системы, у которых установившееся значение регулируемой величины не зависит от нагрузки.

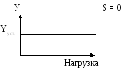
Изменяя характеристики элементов САУ, мы изменяем, только динамику системы, а _уст всегда равна 0. (при X(t)=1)

Особенности астатических систем, работающих в режиме стабилизации (когда Y_уст. = const), является то, что при скачкообразном X_зад статистическая ошибка _уст = X_зад – Y_уст = 0

Особенностью астатических систем является наличие в них интегрирующих элементов, т.е. таких элементов, у которых выходная величина является интегралом от входной величины.

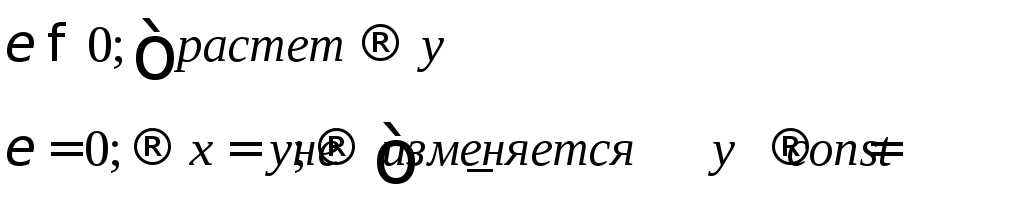
Обыкновенные линейные сау

Как отмечалось выше, под действием управляющих и возмущающих воздействий в системе возникают динамические переходные процессы.

Динамика таких систем описывается дифференциальным уравнением вида:

(1)

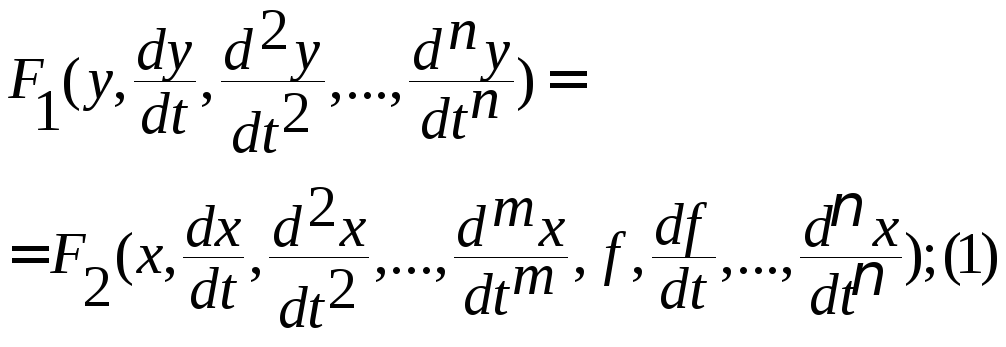
Смысл этого уравнения:

Под действием, управляющего воздействия X и его m производных, а так же под действием возмущающего воздействия f и его производных происходит изменение регулируемой величиныy и ее n производных.

Решение дифференциального уравнения (1) при заданных X , f и начальных условиях - есть переходный процесс в этой системе. Уравнение (1) может быть линейным с постоянными коэффициентами, линейным с переменными коэффициентами, нелинейным, содержать чистое (транспортное) запаздывание и т.д.

Каждый тип уравнения определяет класс САУ. Для каждого класса САУ разрабатываются свои методы исследования. Наиболее полной и простой является теория обыкновенных линейных систем. Вместе с тем с ее помощью можно решить большое количество практически важных задач.

Обыкновенными линейными системами, называются системы, динамические процессы в которых описываются обыкновенными линейными дифференциальными уравнениями с постоянными коэффициентами и все статические характеристики элементов этой системы также линейны.

Статический характеристикой называется зависимость выходной величины от входной на установившемся режиме.

T₂

Линейность статической характеристики понимается в ограниченном смысле. Если рассматривать широкий диапазон изменения входной величины, то статические характеристики большинства элементов будут нелинейными.

U_вых.

Если же входной сигнал изменяется в диапазоне от U₁ до U₂, то можно считать, что статическая характеристика линейна. Замена нелинейной характеристики линейной называется линеаризацией.

Динамика обыкновенных линейных систем в общем виде описывается дифференциальным уравнением вида:

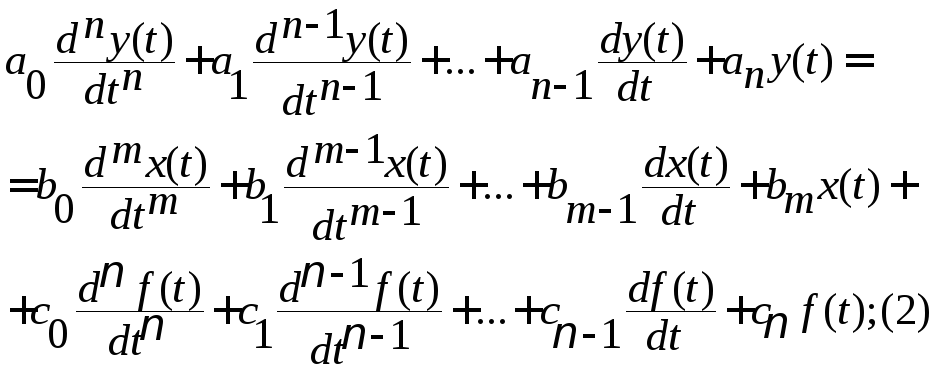
Смысл уравнения (2) такой же, как и уравнения (1).

Здесь - любые целые положительные числа, - постоянные коэффициенты.