
- •Теория автоматического управления
- •Поведение любого оу характеризуется следующими параметрами:
- •Сравнение эффективности работы разомкнутых и замкнутых систем управления
- •Разомкнутая система.
- •Регулятор
- •З fамкнутая система
- •Регулятор
- •Управляемый
- •Работа сау
- •Статические системы.
- •Астатические системы.
- •Обыкновенные линейные сау
- •Составление дифференциальных уравнений сау.
- •Линеаризация дифференциальных уравнений сау разложением в ряд Тейлора.
- •Характеристики сау
- •Частотные характеристики.
- •Переходная функция.
- •Типовые элементарные звенья (тэз)
- •Звено нулевого порядка
- •Звено первого порядка.
- •Звено 2-го порядка.
- •Интегрирующее звено.
- •Дифференцирующее звено
- •Запаздывающее звено.
- •Способы соединения типовых элементарных звеньев (тэз)
- •Устойчивость сау.
- •Необходимые и достаточные условия устойчивости линейных сау.
- •Частотные критерии устойчивости.
- •Критерий устойчивости Михайлова.
- •Качество систем автоматического управления.
Сравнение эффективности работы разомкнутых и замкнутых систем управления
f
u y
Управляемый
объект


Его уравнение имеет вид:
![]() (1)
(1)![]()
![]() -
коэффициент усиления объекта по сигналу
управления,
-
коэффициент усиления объекта по сигналу
управления,
![]() -
коэффициент усиления объекта по отношению
к возмущающему воздействию.
-
коэффициент усиления объекта по отношению
к возмущающему воздействию.
Пусть
![]() >0
и
>0
и![]() >0.
>0.
Перед системой стоит задача воспроизведения входного сигнала х
сигналом у.
Сравним результаты работы разомкнутой и замкнутой систем.
Разомкнутая система.
f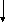
Управляемый объект X U Y
Регулятор




В разомкнутой системе при образовании сигнала управления U не учитывается информация о результатах её работы, т.е. не учитывается текущее значение Y.
Рассмотрим несколько вариантов.
Коэффициенты уравнения (1) известны точно, они стабильны и возмущение f(t)=0,
т.е. уравнение объекта
![]()
Пусть сигнал управления в разомкнутой системе
![]()
![]() .
.
Тогда
![]() и
и
![]() .
.
Таким образом , при отсутствии возмущающих воздействий и при стабильных коэффициентах усиления объекта разомкнутая система работает идеально точно.
Однако такие ситуации в реальной жизни не существуют.
На систему действуют возмущения и параметры системы не стабильны.
Коэффициенты известны точно и возмущение f(t)
 .
Про возмущение
известно,
что
.
Про возмущение
известно,
что
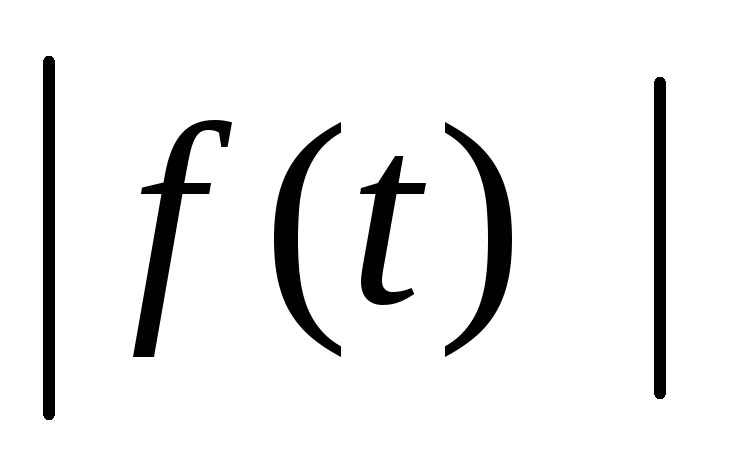
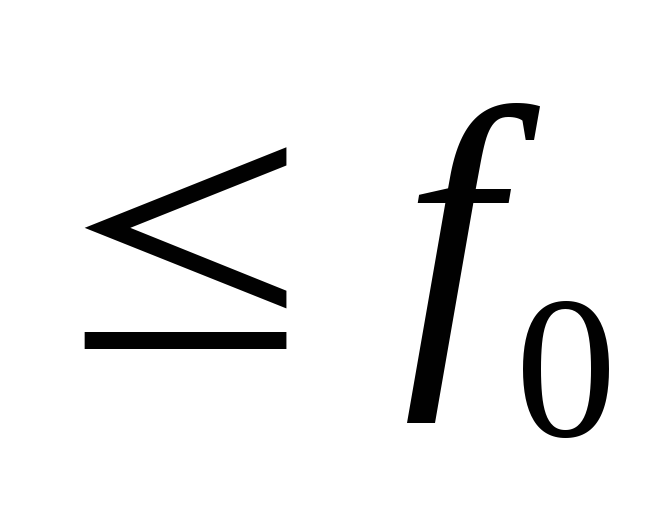 .
.
Поскольку поведение возмущения заранее не известно, выберем по-прежнему
![]() .
.
Тогда в силу уравнения (1) имеем:
![]()
Таким образом, максимальная ошибка будет
![]()
Вывод: в разомкнутой системе при наличии возмущения и при стабильных коэффициентах будет ошибка при воспроизведении входного сигнала. У нас нет возможности повлиять на эту ошибку.
Возмущение отсутствует, т.е. f(t)
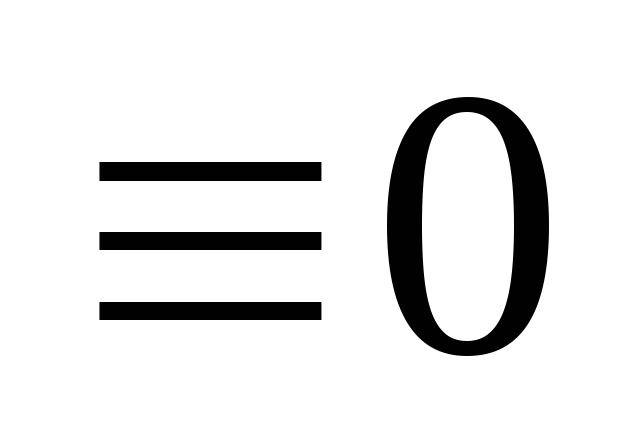 ,
,
коэффициенты
известны не точно и
![]() ошибка в
определении
ошибка в
определении
![]() .
.
Тогда уравнение объекта в действительности
![]()
а
нам кажется, что
![]() .
.
Выбираем
управление
![]() т.к. считаем, что
т.к. считаем, что![]() -
истинное значение коэффициента усиления
объекта по управлению.
-
истинное значение коэффициента усиления
объекта по управлению.
Тогда
![]()
Отсюда
![]()
Если
входной сигнал ограничен по модулю,
т.е.
![]() то максимальное значение ошибки
то максимальное значение ошибки
![]()
Таким образом, и в этой ситуации, когда на систему не действует возмущение, но мы не точно знаем коэффициенты, в разомкнутой системе имеется ошибка.
Самое
неприятное в ошибках, появляющихся в
разомкнутых системах (случаи II и III),
состоит в том, что у нас нет возможности
воздействовать на них, т.к. они зависят
от параметров, которыми мы не можем
управлять: кu
и кf
– это
характеристики объекта, f0
–
возмущение,
![]() -
нестабильность коэффициента усиления
объекта по управляющему воздействию.
-
нестабильность коэффициента усиления
объекта по управляющему воздействию.
З fамкнутая система
x y
объект u
Регулятор
Управляемый
(-)






Объект тот же самый- описывается тем же уравнением:
![]() (1)
(1)
Закон управления выбираем таким, чтобы он зависел от результата работы системы:
![]() (2)
(2)
где
![]() коэффициент
усиления регулятора,
коэффициент
усиления регулятора,
![]() >0,
>0,
![]() (3)
(3)
Для
получения уравнения замкнутой системы
исключим из уравнений (1), (2), (3)
![]() и
и![]() .
.
Тогда
![]()
Обозначим
![]() -
коэффициент усиления системы.
-
коэффициент усиления системы.
Отсюда
![]()
![]() , (4)
, (4)
и
![]() .
(5)
.
(5)
Рассмотрим те же три случая.
I.
Коэффициенты
известны точно и стабильны и
![]()
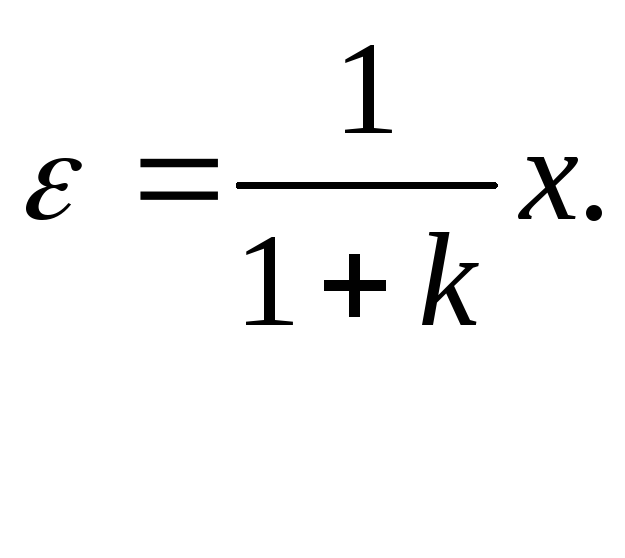
Этот результат хуже, чем у разомкнутой системы в этом случае.
Но
если
![]() <
<![]() ,
то увеличивая
,
то увеличивая![]() ,
а, следовательно, и
,
а, следовательно, и![]() ,
уменьшаем ошибку
,
уменьшаем ошибку![]() .
.
II
.Коэффициенты
известны точно и стабильны,
![]() При этом
При этом![]() <
<![]() .
.
Тогда ![]() .
.
Если
в случае разомкнутой системы у нас не
было возможности повлиять на величину
![]() ,
то в замкнутой системе увеличивая
,
то в замкнутой системе увеличивая![]() ,
можно уменьшить
,
можно уменьшить![]() .
.
Возмущение отсутствует, т.е.
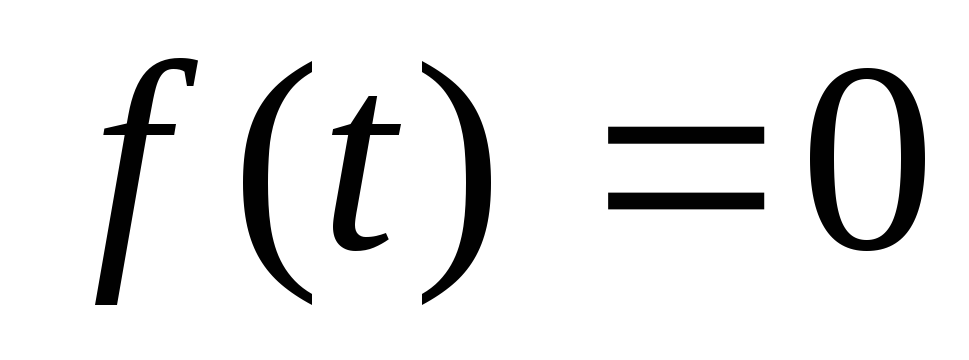 ,
а коэффициенты нестабильны:
,
а коэффициенты нестабильны:
![]() .
.
Тогда
![]()
![]()
и ![]() .
.
Отсюда
![]()
и ![]() .
.
В
этой ситуации также увеличивая
![]() ,
уменьшаем
,
уменьшаем![]() .
.
Таким образом, сравнивая работу разомкнутой и замкнутой систем,
видим, что в разомкнутой системе нет инструмента воздействия на ошибку. В замкнутой системе, изменяя параметры регулятора, можно уменьшать ошибку воспроизведения входного сигнала.
Функциональная схема системы автоматического управления (САУ)
Любая САУ , вне зависимости от того, какую конкретную задачу выполняет, из каких объектов управления и элементов состоит, может быть представлена следующей функциональной схемой.
F1
Y(t)
1 U(t)




F2
2

 F6
F5
F6
F5
4
4 3
6
5
 Z(t)
E(t)
X(t)
Z(t)
E(t)
X(t)







F3 F4
7


F7
1 – объект управления, основной элемент САУ. Это любое техническое устройство и т.д . (см. выше), требуемый режим работы которого должна поддерживать САУ.
![]() - регулируемая величина. Если
- регулируемая величина. Если![]() скалярная величина, то САУ – одномерная,
если это вектор , то САУ – многомерная.
скалярная величина, то САУ – одномерная,
если это вектор , то САУ – многомерная.
Все остальные элементы САУ образуют регулятор.
2- измерительное устройство (чувствительный элемент, датчик) предназначается для измерения регулируемых параметров и преобразования их в сигналы , удобные для дальнейшего использования в процессе управления. Чувствительный элемент должен удовлетворять определенному классу точности.
3. Задающее устройство – вырабатывает сигнал, пропорциональный заданному значению регулируемой величины. Сигналы на выходе элементов 3 и 2 должны быть одинаковой физической природы.
- Если X(t) = const, то это – система стабилизации.
- Если X(t) является заранее известной функцией, то это – система программного управления
- Если X(t) - неизвестная функция, то это – следящая система
- Адаптивные системы - системы, которые подстраиваются под изменение каких-то параметров.
- Системы экстремального регулирования – системы, которые должны обеспечивать экстремум выходной величины.
4.
Сравнивающее устройство - сравнивает
заданное и действительное значения
регулируемой величины и формирует
сигнал рассогласования
![]() .
.
5.
Управляющее устройство формирует закон
управления, то есть реализует различные
математические
операции с
![]() .
.
![]() то
это – пропорциональный регулятор
то
это – пропорциональный регулятор
![]()
![]() то
это – интегрирующий регулятор
то
это – интегрирующий регулятор
![]()
![]() то
это – дифференцирующий регулятор
то
это – дифференцирующий регулятор
![]()
Возможны комбинации регуляторов ПИ, ПД, ИД. ПИД.
6. Исполнительное устройство – преобразовывает сигнал управления в перемещение регулирующего органа.
7. Местная обратная связь.
F1, …, Fi – нежелательные воздействия, которые называются возмущающими воздействиями. СУ должна быть организована таким образом чтобы, несмотря на возмущения, она бы справлялась с задачами управления.
