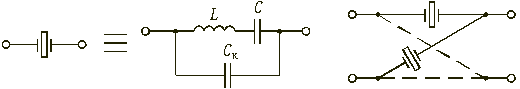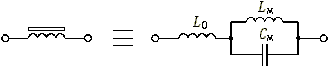- •17.2. Аппроксимация характеристик фильтров нижних частот
- •17.3. Реализация фильтров нижних частот
- •17.4. Переход от фильтров нижних частот к другим типам фильтров
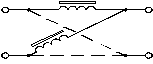
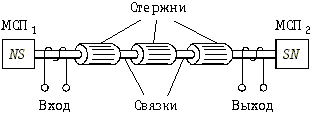
- •17.5. Резонаторные фильтры
- •Цифровые фильтры
- •19.6. Дискретные фильтры и их синтез
- •19.3. Z-преобразование и его свойства
- •19.4. Дискретные цепи
- •19.5. Типовые звенья дискретных цепей
- •19.6. Дискретные фильтры и их синтез
- •19.7. Цифровые фильтры
- •Вопросы и задания для самопроверки
- •Глава 18. Корректирующие цепи и их синтез
- •18.1. Принцип корректирования искажений
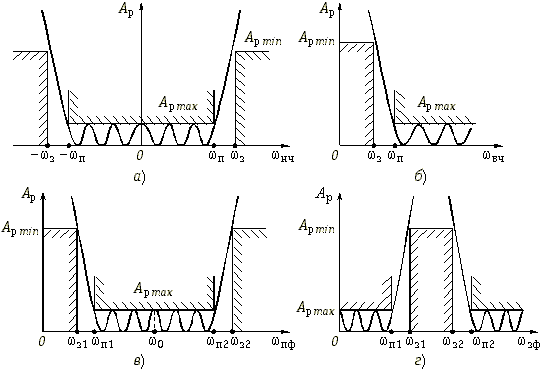
17.4. Переход от фильтров нижних частот к другим типам фильтров
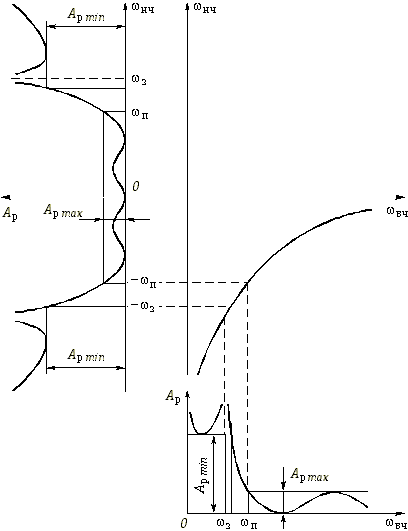
Преобразование шкалы частот ФНЧ.
|
|
|
Рис. 17.16 |
![]() (17.31)
где
(17.31)
где
![]() n
– граничная частота полосы пропускания
ФНЧ и ФВЧ.
n
– граничная частота полосы пропускания
ФНЧ и ФВЧ.
![]() н.ч
= —
н.ч
= —![]() частоте
частоте![]() в.ч
= 0; частоты
в.ч
= 0; частоты
![]() н.ч
= —
н.ч
= —![]() п
частоте
п
частоте
![]() в.ч
=
в.ч
=
![]() п;
частоты
п;
частоты
![]() н.ч
= 0 частоте
н.ч
= 0 частоте
![]() в.ч
=
в.ч
=
![]() .
.
|
|
|
Рис. 17.17 |
:
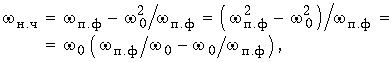 (17.32)
где
(17.32)
где![]() ;
;![]() п1
и
п1
и
![]() п2
– граничные частоты полосы
п2
– граничные частоты полосы
|
|
|
Рис. 17.18 |
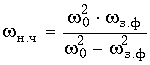 (17.33)
(17.33)
Преобразование схем
пассивных LC-фильтров.
![]() ,
т.
е. в емкостное сопротивление ФВЧ, гдеCв.ч
= 1/
,
т.
е. в емкостное сопротивление ФВЧ, гдеCв.ч
= 1/![]() п2Lн.ч.
п2Lн.ч.
Емкостная
проводимость:
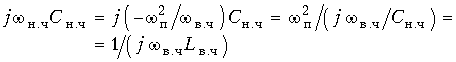 переходит
в индуктивную проводимость фильтра ВЧ
с индуктивностьюLв.ч
= 1/
переходит
в индуктивную проводимость фильтра ВЧ
с индуктивностьюLв.ч
= 1/
![]() п2Cн.ч.
п2Cн.ч.
Преобразование частоты
(17.32) приводит к замене индуктивного
сопротивления ФНЧ:
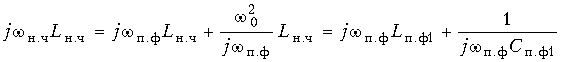
сопротивлением
последовательного контура в ПФ с
элементами Lп.ф1
= Lн.ч
и Cп.ф1
= 1/ (![]() 02Lн.ч).
02Lн.ч).
Емкостная проводимость
ФНЧ:
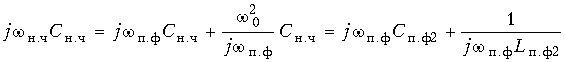 заменяется
в ПФ проводимостью параллельного контура
с элементамиCп.ф2
= Cн.ч
и Lп.ф2
= 1/ (
заменяется
в ПФ проводимостью параллельного контура
с элементамиCп.ф2
= Cн.ч
и Lп.ф2
= 1/ (![]() 02Cн.ч).
02Cн.ч).
![]()
Преобразование
передаточных функций активных RC-фильтров.
![]() или
или![]() (17.34)
где
(17.34)
где![]() н.ч
=
н.ч
=
![]() н.ч/
н.ч/![]() п
и
п
и
![]() в.ч
=
в.ч
=
![]() в.ч/
в.ч/
![]() п.
п.
![]() (17.35)
(17.35)
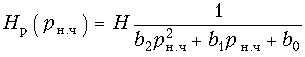 (17.36)
(17.36)
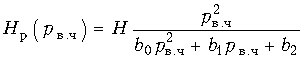 (17.37)
(17.37)
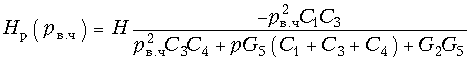 (17.38)
(17.38)
|
| |
|
Рис. 17.20 |
Рис. 17.21 |
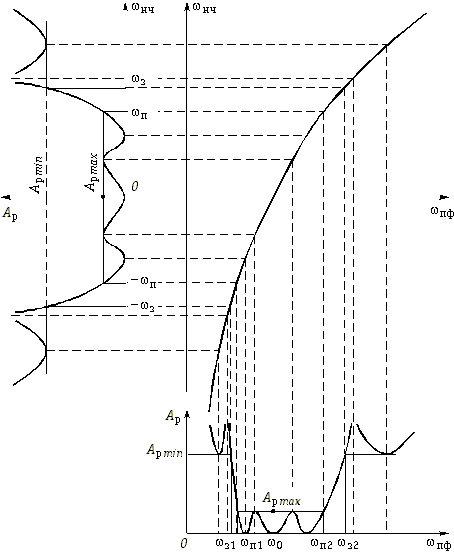
Для перехода от
НЧ-прототипа к полосовому фильтру
воспользуемся (17.33):
![]() или
или![]() (17.39)
где
(17.39)
где![]() н.ч
=
н.ч
=
![]() н.ч
н.ч![]() п;
п;
![]() п.ф
=
п.ф
=
![]() п.ф/
п.ф/![]() п;
п;
![]() 0
=
0
=
![]() 0/
0/![]() п.
п.
Вводя переменную p
= j![]() и учитывая, что p2
= –
и учитывая, что p2
= –![]() 2,
находим из (17.39):
2,
находим из (17.39):
![]() (17.40)
(17.40)
Такая замена переменной
pн.ч
в (17.36) приводит к передаточной функции
полосового фильтра:
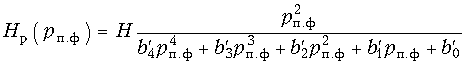 (17.41)
гдеb'4
= b2;
b'3
= b1;
b'2
= 2b2
(17.41)
гдеb'4
= b2;
b'3
= b1;
b'2
= 2b2![]() 02
+ b0;
b'1
= b1
02
+ b0;
b'1
= b1![]() 02;
b'0
= b2
02;
b'0
= b2![]() 04.
04.
Видим, что при переходе к ПФ порядок передаточной функции удваивается. Передаточную функцию (17.41) можно разбить на произведение передаточных функций второго порядка и каждую из них реализовать отдельной ARC-схемой.
Запишем передаточную
функцию ПФ второго порядка:
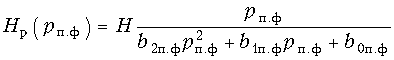 (17.42)
(17.42)
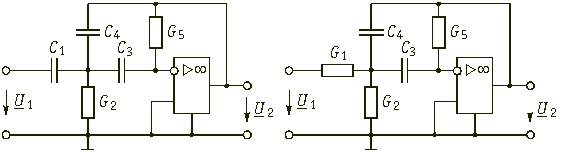
Подобную передаточную
функцию имеет ARC-схема,
изображенная на рис. 17.14, б
при Y1
= G1,
Y2
= G2,
Y5
= G5
и Y3
= = pC3,
Y4
= pC4.
Действительно, из (17.28) находим:
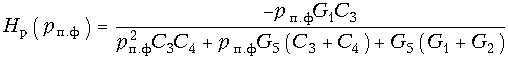 (17.43)
(17.43)
Элементы схемы фильтра (рис. 17.21) определяются сопоставлением (17.42) и (17.43).
Порядок синтеза ФВЧ, ПФ и ЗФ.
17.5. Резонаторные фильтры
|
| |||
|
Рис. 17.22 |
Рис. 17.23 | ||
|
|
| ||
|
Рис. 17.25 |
| ||
|
|
|
| |
|
Рис. 17.25 |
Рис. 17.26 |
| |
Цифровые фильтры
Функциональная схема цифрового фильтра.
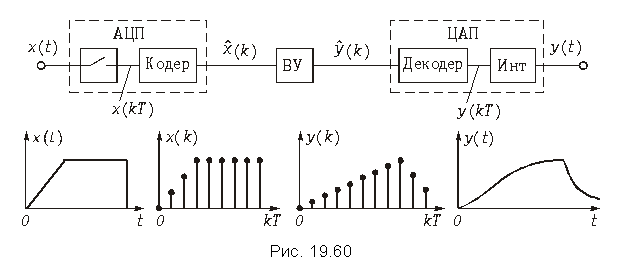
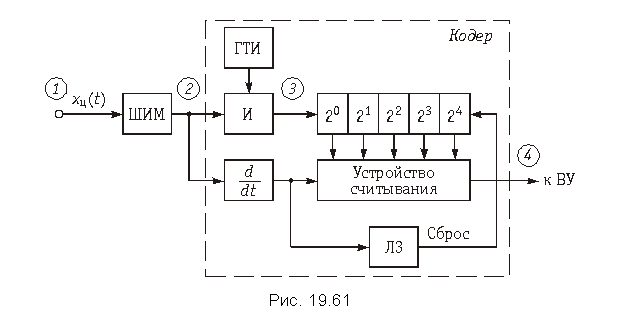 Аналогово-цифровое
преобразование сигналов.
Аналогово-цифровое
преобразование сигналов.
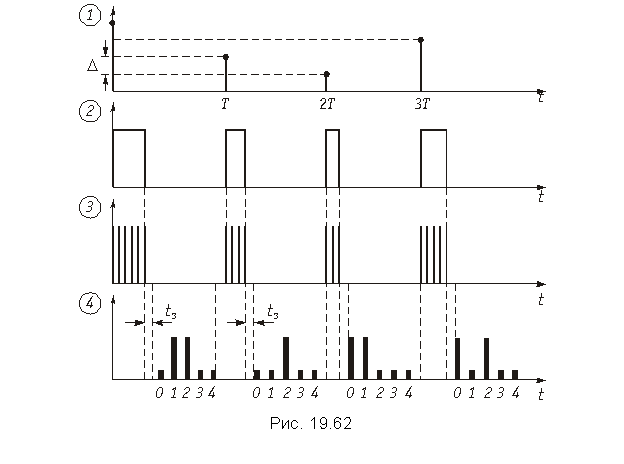
![]()
где N – число разрядов в бинарном коде. Причем E > umax, где umax – максимально возможное значение кодирующего сигнала.
Шумы квантования.
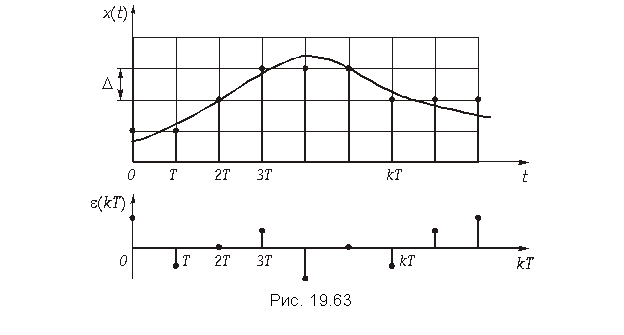
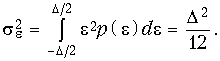 (19.58)
(19.58)
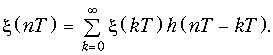 (19.59)
(19.59)
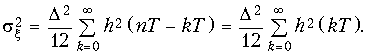 (19.60)
(19.60)
Ошибки округления.
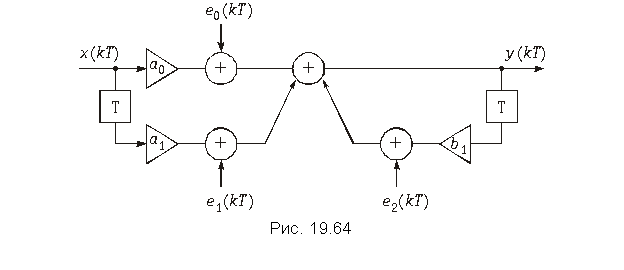
![]()
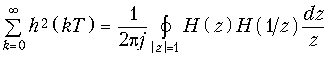 (19.61)
(19.61)
из уравнения
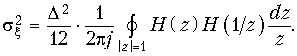 (19.62)
(19.62)
Пример.
Определить дисперсию шума на выходе
![]() ЦФ
1-го порядка с передаточной функцией
ЦФ
1-го порядка с передаточной функцией
![]()
Для нахождения
![]() воспользуемся
формулой (19.62):
воспользуемся
формулой (19.62):
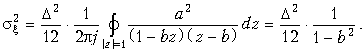
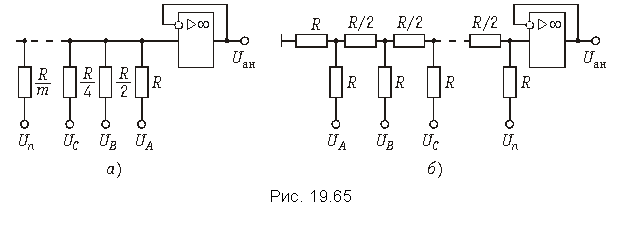
Цифро-аналоговое преобразование.
![]()
![]()
Интерполяторы.