17.1. Классификация фильтров Рис. 17.1 . Рис. 17.2 Рис. 17.3

17.2. Аппроксимация характеристик фильтров нижних частот

Функция фильтрации. В общем виде электрические фильтры описываются передаточной функцией вида: 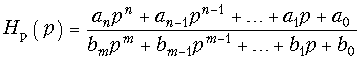(17.1)

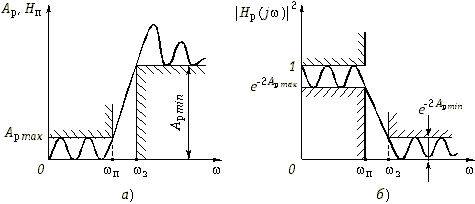
Квадрат амплитудно-частотной характеристики таких фильтров (17.2) и, следовательно, рабочее ослабление(17.3), где– нормирующая частота.

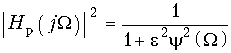(17.4)(17.5)

Функция называется функцией фильтрации, а– коэффициентом неравномерности ослабления

удовлетворяющая условиям: –1 1 в полосе пропускания и>> 1 в полосе непропускания фильтра.

Фильтры Баттерворта. Если в выражениях, описывающих квадрат АЧХ фильтра (17.4) и его рабочее ослабление (17.5), в качестве функции фильтрации используются полиномы Баттерворта =B_m() =^m

(= 1) выполнения равенстваА_р()₌₁ = А_рmax или |H_р(j)|=. Отсюда с учетом (17.5) или (17.4) имеем 1 +² = и² = – 1. Вычисленный таким способом коэффициент:(17.6) называетсякоэффициентом неравномерности ослабления в полосе пропускания фильтра.

В формуле (17.6) величина А_рmax имеет размерность непер. Если воспользоваться значениями А_рmax в децибелах, то (17.7)

(17.8)

Рабочее ослабление фильтра Баттерворта: (17.9)

Рис. 17.4

_з  А_р(_з) А_рmin или |H_р (j)|. С учетом этого условия получим 1 +²>, откуда.

Величина А_рmin входит в формулу в неперах. Если вычислять ее в децибелах, то: m (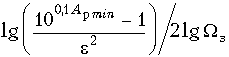17.11)

(17.12) иk = 1, 2, ..., 2m.

Так как: , имеем:(17.13)

Для нечетных значений m:

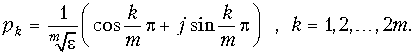
Выражение (17.12) примет вид: .

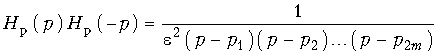, где H = 1/.

Пример. Найти выражения для частотной характеристики и передаточной функции фильтра нижних частот Баттерворта, удовлетворяющего следующим требованиям: А_рmax = 3 дБ; А_рmin = 12,2 дБ; f_п = 159 кГц; f_з = 318 кГц.

Определим нормированную частоту _з = f_з/f_n = 2 и по формуле (17.7) коэффициент неравномерности ослабления ² = 10^0,1×3 – 1 = 1. Порядок фильтра найдем согласно (17.11): .

Выберем m = 2. Тогда в соответствии с (17.8) и (17.9):

17.3. Реализация фильтров нижних частот

Лестничные полиномиальные LC-фильтры.

Рис. 17.10

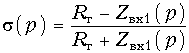(17.25)

: (17.26)

(17.27)

Лестничные фильтры со всплесками ослабления.

Рис. 17.13

Реализация лестничных фильтров по каталогам.

Таблица 17.1 Параметры элементов фильтров Золотарева четвертого порядка

s	As, дБ	С1	С2	L2		С3	L4
при As = 0,028 дБ
3,98 3,39 2,96 2,63	56 50 45 41	0,7020 0,6871 0,6697 0,6497	0,04232 0,05952 0,08025 0,1049	1,241 1,215 1,186 1,152	4,364244 3,718173 3,241901 2,876673	1,282 1,272 1,261 1,248	0,7429 0,7440 0,7451 0,7465
при As = 0,044 дБ
3,76 3,23 2,84 2,45	56 50 45 40	0,7575 0,7422 0,7245 0,6968	0,044585 0,06339 0,08436 0,1183	1,282 1,256 1,226 1,287	4,124781 3,544141 3,109875 2,677264	1,326 1,316 1,305 1,287	0,8018 0,8027 0,8037 0,8052
при As = 0,099 дБ
3,39 2,96 2,53 2,22	56 51 45 40	0,8775 0,8612 0,8357 0,8057	0,05363 0,07202 0,1017 0,1382	1,349 1,321 1,278 1,229	3,718173 3,241901 2,773213 2,427221	1,400 0,390 1,373 1,354	0,9292 0,9297 0,9304 0,9311
при As = 0,177 дБ
3,09 2,73 2,37 2,09	55 50 45 40	0,9807 0,9630 0,9356 0,9040	0,063309 0,08273 0,1141 0,1522	1,382 1,353 1,308 1,257	3,386078 2,988543 2,588050 2,286311	1,443 1,432 1,414 1,394	1,041 1,041 1,041 1,041
s	As, дБ	L1	L2	С2		L3	С4

Активные RC-фильтры. (17.28)

Рис. 17.14

(17.29)

(17.30)