3.2.2.3 Консервативное звено

Это звено получается при мнимых полюсах передаточной функции (3.1), и его можно рассматривать как частный случай колебательного звена при . Выражения для передаточной и некоторых частотных функций звена будут иметь вид:

,

, ,

.

На рис. 3.13, аизображены логарифмические частотные характеристики консервативного звена. Точная ЛАЧХ (сплошная линия) терпит разрыв непрерывности второго рода на частоте сопряжения, асимптотическая ЛАЧХ (пунктирная линия) такая же, как у колебательного звена. ЛФЧХ в точкетерпит разрыв непрерывности первого рода (фаза скачком изменяется от 0 до).

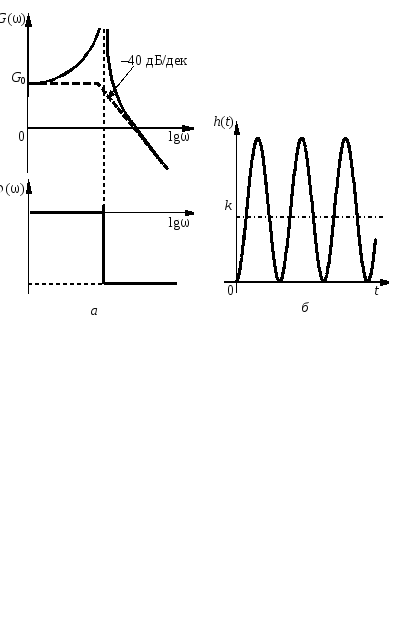Рис. 3.13 — ЛАЧХ, ЛФЧХ (а), переходная характеристика (б)

консервативного звена

Переходная функция консервативного звена может быть получена по формуле (2.10) при мнимых полюсах и имеет вид

.

На рис 3.13, б показана переходная характеристика консервативного звена, она представляет собой незатухающие автоколебания частотой и амплитудой.

Консервативное звено на пассивных четырехполюсниках не реализуется. Если обратиться к приведенному выше примеру (см. рис. 2.6), то должны отсутствовать потери в контуре, т.е. выполняться условие , что физически невозможно. В устройстве, схема которого приведена на рис. 3.12, а, в соответствии с формулами (3.5) получение консервативного звена возможно при . Для этого резисторпросто нужно удалить из устройства.

3.3 Особые звенья линейных сау

3.3.1 Неминимально-фазовые звенья

В ряде устройств, например при мостовых соединениях, процессы описываются дифференциальным уравнением, имеющим отрицательные коэффициенты в правой части:

.

Передаточная функция такого звена будет иметь вид

,

т.е. имеет положительный нуль .

Такие звенья относятся к устойчивым неминимально-фазовым звеньям первого порядка, их характеристики похожи на характеристики инерционного форсирующего звена.

Пример 3.5

На рис. 3.14 приведена мостовая схема, в которой выполняется соотношение . Для нее будет иметь место соотношение:

т.е.

где .

Рис. 3.14 — Пример неминимально-

фазового устойчивого звена

На рис. 3.15, а показаны логарифмические частотные характеристики этого звена при . Его ЛАЧХ не отличается от ЛАЧХ инерционного форсирующего звена при, а ЛФЧХ изменяется в диапазоне. Переходная характеристика (рис. 3.15, б) имеет при скачок в отрицательном направлении.

Рис. 3.15 — Характеристики устойчивого

неминимально-фазового звена

Неустойчивые неминимально-фазовые звенья содержат в передаточных функциях положительные полюсы. Примером такого звена может служить асинхронный двигатель, работающий в режиме максимального скольжения. Другой пример — охват минимально-фазового звена положительной обратной связью.

Пусть инерционное звено с передаточной функцией охвачено положительной обратной связью с коэффициентом передачи(рис. 3.16, а). Передаточная функция получившегося эквивалентного звена будет иметь вид:

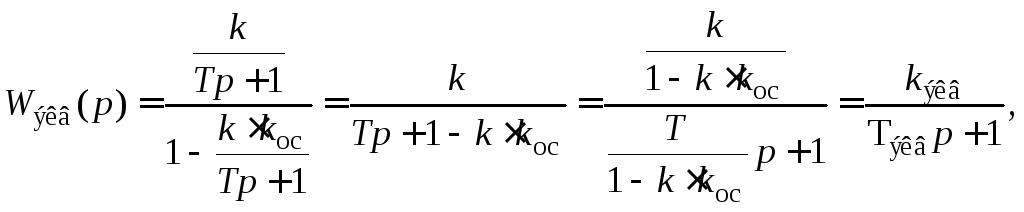
где .

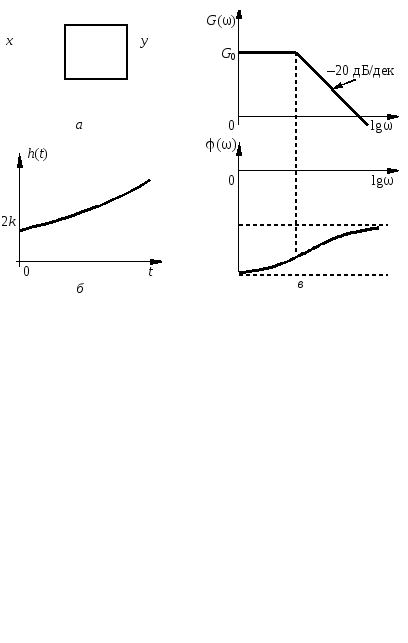
Рис. 3.16 — Неустойчивое неминимально-фазовое звено (а)

и его характеристики (б, в)

При величиныстановятся отрицательными и передаточная функциястановится такой, что ее полюсбудет положительным.

На рис. 3.16, б приведена переходная характеристика этого звена, она неограниченно нарастает, начиная со значения , поскольку рассчитывается по формуле. ЛАЧХ неустойчивого неминимально-фазового звена такая же, как и у инерционного звена, а ЛФЧХ, рассчитываемая по выражению , возрастает со значениядо(см. рис. 3.16, в).