3.2.1.5 Форсирующее звено

Часто в литературе это звено именуется как пропорционально-дифференцирующее. Выходная величина этого звена пропорциональна входной и производной от входной величины. Передаточная функция и основные частотные функции:

Звено характеризуется двумя параметрами — коэффициентом передачи и постоянной дифференцирования.

На рис. 3.5, а—в приведены частотные характеристики форсирующего звена, они являются обратными характеристикам инерционного звена. АФЧХ (рис. 3.5, а) имеет вид вертикальной прямой, расположенной в первом квадранте комплексной плоскости на расстоянии от начала координат. АЧХ (рис. 3.5, б) монотонно возрастает с ростом частоты, начиная со значения . Низкочастотные асимптоты ЛАЧХ форсирующего (рис. 3.5, в) и инерционного звеньев совпадают, но высокочастотная асимптота ЛАЧХ форсирующего звена имеет наклон плюс 20 дБ/дек. Частота сопряжения равна . ЛФЧХ форсирующего звена точно такая же, как и у инерционного, только фаза имеет положительные значения.

На рис. 3.5, г приведена схемная реализация форсирующего звена на операционном усилителе (на пассивных четырехполюсниках это звено не реализуется). Поскольку в схеме

,

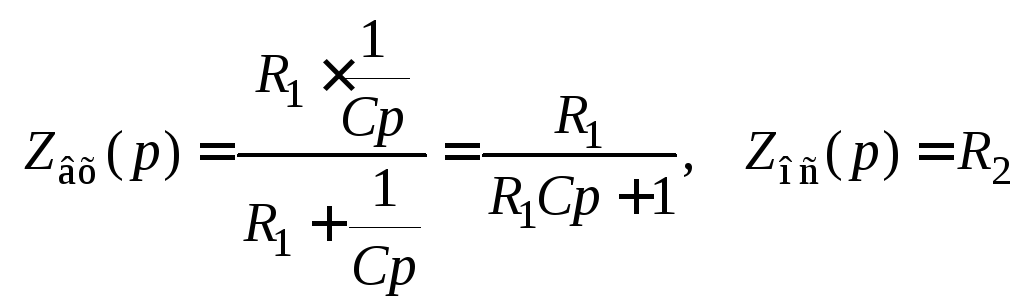то ,

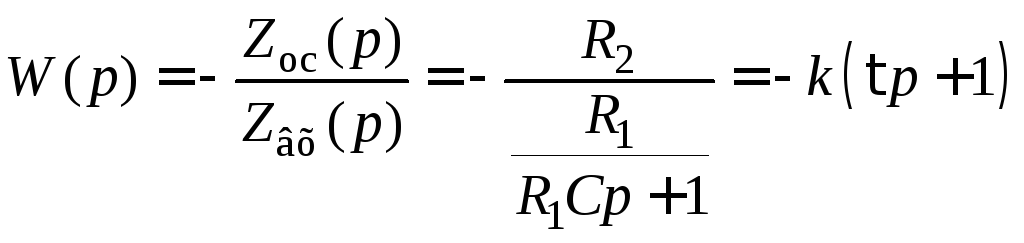где .

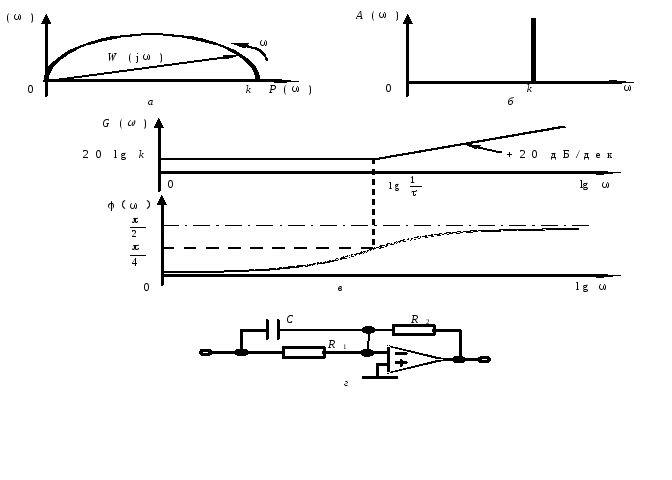
Рис. 3.5 — Частотные характеристики форсирующего звена (а—в)

и его реализация на операционном усилителе (г)

Переходная характеристика форсирующего звена , т.е. равна сумме переходных характеристик дифференцирующего и пропорционального звеньев. В начальный момент времени она имеет скачок бесконечной амплитуды, как и у идеального дифференцирующего звена, а далее проходит горизонтально, как и у пропорционального звена.

Остальные звенья первого порядка образованы путем последовательного соединения рассмотренных звеньев, и их относят к типовым ввиду широкого применения в САУ.

3.2.1.6 Инерционное форсирующее звено

Это звено представляет последовательное соединение инерционного и форсирующегозвеньев, поэтому их передаточные функции и АЧХ перемножаются, т.е.

,

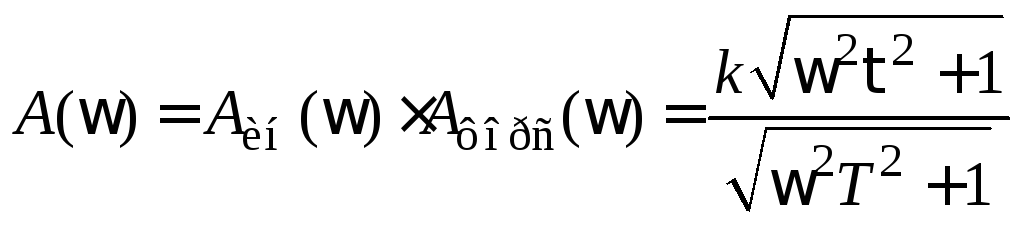а ЛАЧХ и ЛФЧХ — складываются:

.

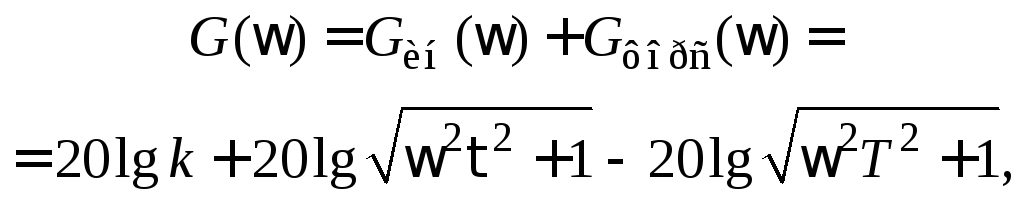
На рис. 3.6, а, б изображены логарифмические частотные характеристики инерционного форсирующего звена, их вид существенно зависит от соотношения постоянных времени и. При(рис. 3.6, а) ЛАЧХ имеет наклон –20 дБ/дек после частоты сопряжения и нулевой наклон послечастоты сопряжения . При(рис. 3.6, б) ее наклон +20 дБ/дек после частоты сопряжения и нулевой наклон после. ЛФЧХ в результате суммирования составляющихи(на рис. 3.6, а, б они показаны штрихпунктирными линиями) имеет колоколообразную форму.

Расчетное выражение для переходной функции инерционного форсирующего звена может быть получено по формуле (2.15) при ,,,:

.

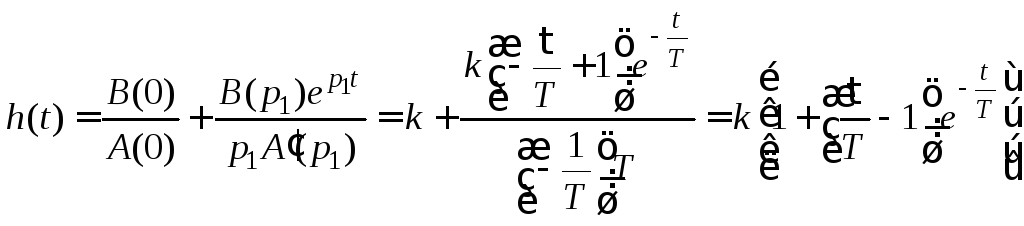При переходная характеристика будет иметь начальный скачок, равный, а приустановившееся значение. Если, скачок на переходной характеристики (рис. 3.6, в) будет меньше установившегося значения, а при скачок на переходной характеристике (рис. 3.6, г) превышает установившееся значение.

Схемная реализация инерционного форсирующего звена также зависит от соотношения и. На рис. 3.6, д приведена его реализация на операционном усилителе при , для этой схемы.

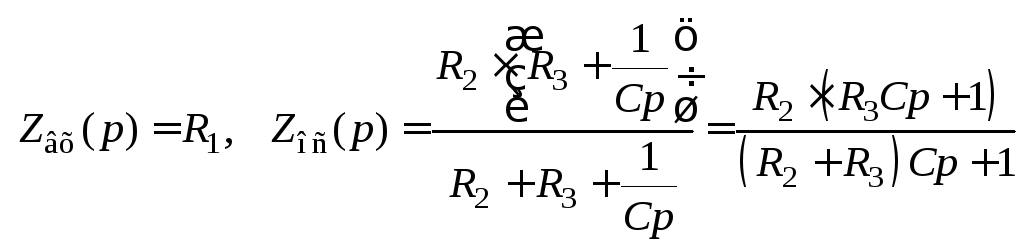Передаточная функция

,

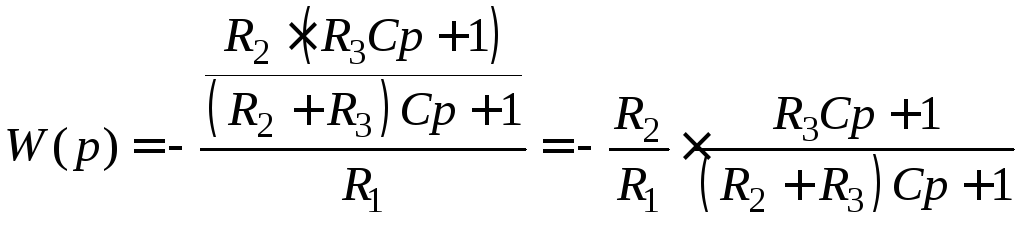то есть ,,.

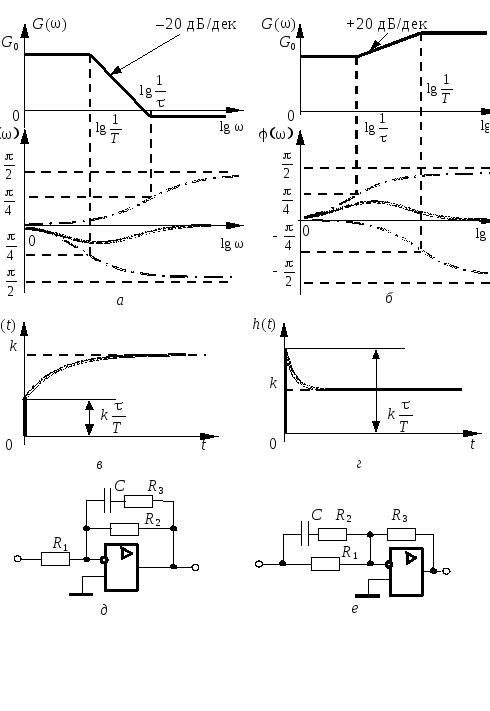
Рис. 3.6 — ЛАЧХ и ЛФЧХ (а, б), переходные характеристики (б, в)

инерционного форсирующего звена (а—в) и варианты

его реализации на операционном усилителе (г, е)

В схеме на рис. 3.6, е , и для такого звена,,.