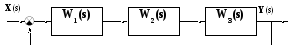Инерционное (апериодическое) звено первого порядка

Передаточная функция инерционного звена равна

.

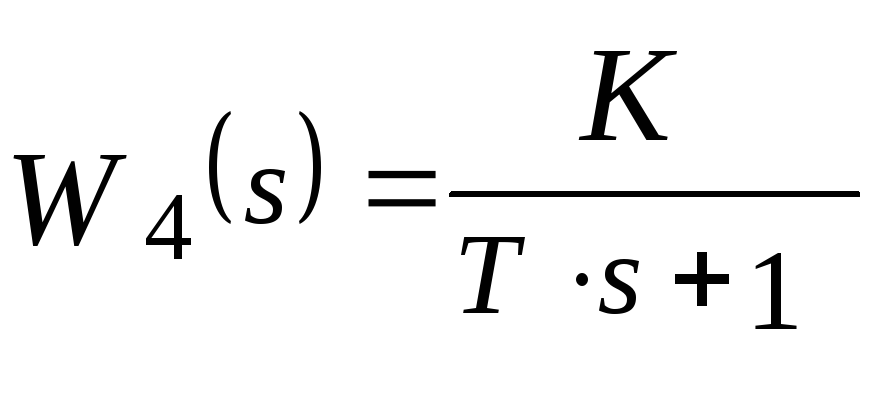Комплексный коэффициент передачи звена будет:

Для нахождения вещественной и мнимой частотных характеристик инерционного звена представим это выражение в следующем виде: отсюда получим вещественную и мнимую частотные характеристики инерционного звена,. Из полученных зависимостей следует, что функция- четная, а функция- нечетная.

Для нахождения годографа АФЧХ инерционного звена, зависимости Q₄() отP₄(), найдем уравнение в функции от переменныхи.

Получим . Подставляя это выражение в формулу дляQ₄(), находим: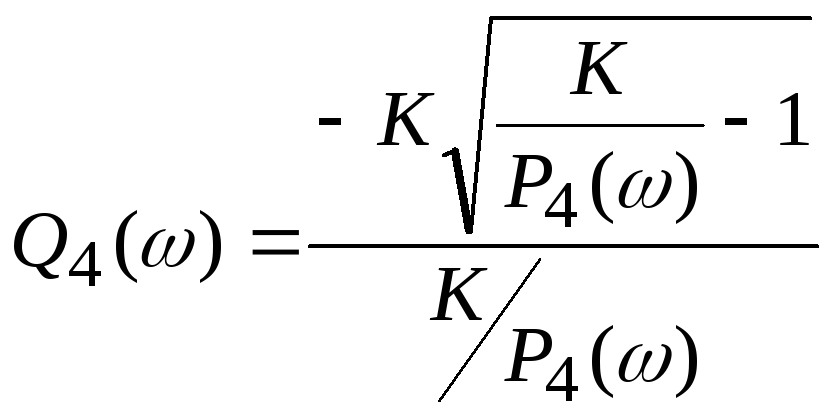. Преобразуя эту зависимость, имеем:. Таким образом, годограф амплитудно-фазовой частотной характеристики (АФЧХ) инерционного звена представляет собой окружность

Учитывая известную связь между частотными характеристиками найдем амплитудно-частотную и фазовую частотные характеристики:

.

Действительная логарифмическая амплитудная частотная характеристика равна

Характеристика имеет низкочастотнуюи высокочастотнуюасимптоты, которые сопрягаются на частоте сопряжения.

Низкочастотная асимптота ЛАЧХ инерционного звена представляет собой предел, при этом и второе слагаемое ЛАЧХ равно нулю.

Высокочастотная асимптота ЛАЧХ находится как из условия . Тогдаи

.

Асимптотической ЛАЧХ является характеристика, составленная из асимптот - двух прямых линий:и

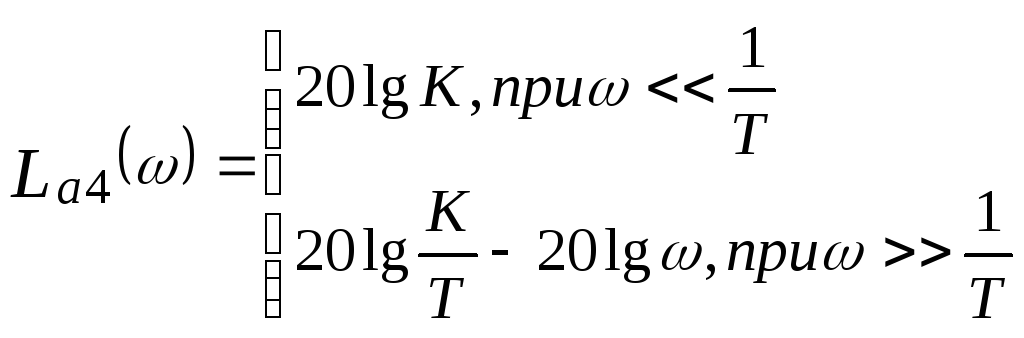
Графики и показаны на рис. 5.7.

Эти характеристики имеют следующие особенности:

низкочастотная асимптота имеет 0 наклон,

высокочастотная асимптота имеет наклон–20 дБ/дек,

асимптоты и сопрягаются на частоте сопряжения .

фазочастотная характеристика на частоте сопряжения принимает значение

при уменьшении частоты относительно частоты сопряжения фазочастотная характеристика стремиться к нулю;

при увеличении частоты относительно частоты сопряжения фазочастотная характеристика стремиться к значению.

рис. 5.7. Асимптотическая логарифмическая амплитудная частотная характеристика инерционного звена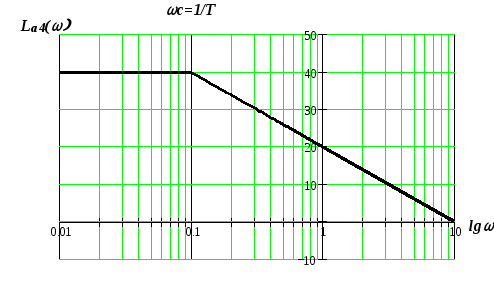

Для оценки неизвестных значений параметров KиTпо ЛАЧХ необходимо построить низкочастотную асимптоту, имеющую нулевой наклон, и высокочастотную асимптоту, имеющую отрицательный наклон -20 дБ/дек. Точка пересечения этих асимптот дает частоту сопряженияи ординату, соответствующую значению, т.е. на частотезначениеравно.

Параметр Kнаходится по формуле.

для определения значенияTнужно воспользоваться выражениемили,.

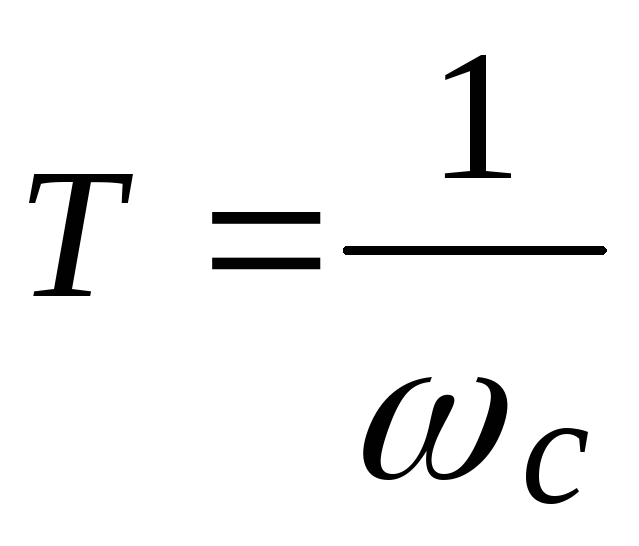Пример расчета асимптотических логарифмических частотных характеристик. Задана передаточная функция инерционного типового звена первого порядка: W(s)=k/(Ts+1), требуется рассчитать и построить асимптотическую ЛАЧХ.

Решение.

1. Заменимsнаjωс учетом того, чтои путем несложных преобразований получим :W(jω)=k/(T jω+1)

2. Запишем выражение амплитуды W(ω):

3.Запишем выражение ЛАЧХL(ω):

Следовательно, в низкочастотной области

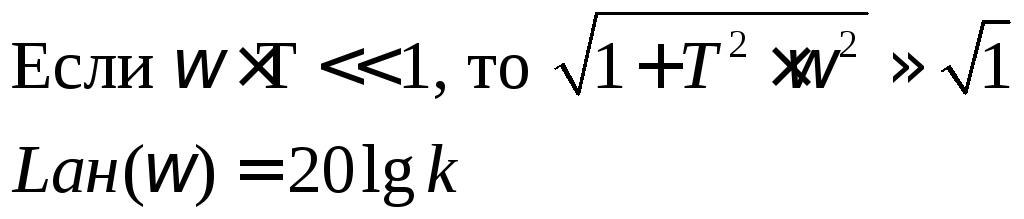
Следовательно, в области высокой частоты

4. Частоты, соответствующие точкам сопряжения отрезков, называются сопрягающими и обозначаютсяω_с=1/Т

5. Строим график ЛАЧХ:

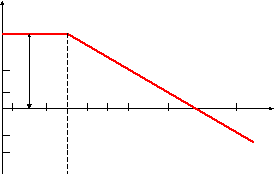L(), дБ

20

20lgk -20дБ\дек

10

lg

0,1 0,5 ω_с=1/Т 1 2 5 10 100

-10

-20 Низкочастот- Высокочастотная область

ная область

Порядок выполнения работы

В соответствии с вариантом задания в табл.4.1. произвести построение частотных характеристик типовых звеньев первого порядка и графоаналитическим способом рассчитать их параметры.

Вычисление частотных характеристик звена или системы

Пусть задана передаточная функция звена, например:

Найдём комплексный коэффициент передачи, заменив переменную sнаj Для этого введём мнимую единицу.

Для этого заменим s(оператор Лапласа) на (jω) :с учетом того, чтои путем несложных преобразований - подстановку комплексной переменной и перемножение числителя и знаменателя на комплексно сопряженное число получим:

,

Избавляясь от мнимой единицы jв знаменателе (иррациональности), получаем комплексный коэффициент передачи в виде:

.

Вещественная часть ККП:	Мнимая часть ККП:
.	.

Запишем комплексный коэффициент передачи формальной заменой sнаjω в передаточной функции разомкнутой системы и выведем полученное выражение на экран с помощью «символьной стрелки», вызываемой также из палитрыСимвольные операторы:

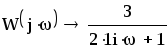
Для нахождения вещественной и мнимойчастотных характеристик звена воспользуемся стандартными функциямиMathcad: Re()иIm()соответственно:

,

Для нахождения вещественной и мнимой частей выражения в Mathcadимеются специализированные встроенные функции:

Выбрать из командной строки опцию «вставка функции» f(x)и из предложенного списка слева – категория функции – комплексные числа (Complex Number), из предложенного списка справа – имя функцииRe() илиIm() – далее клик по кнопке «ОК» или «добавить».

Однако возможности Mathcadне позволяют сразу получить комплексный коэффициент передачи в виде суммы вещественной и мнимой частей.

При этом следует учесть, что комплексный коэффициент передачи может быть представлен в виде

,

где - вещественная часть комплексного коэффициента передачи,

- мнимая часть комплексного коэффициента передачи.

Тогда мнимая и вещественная части будут равны:

Для построения годографа АФЧХ звена зададим диапазон и шаг изменения аргумента (частоты), воспользовавшись знаком «многоточие», вызываемым с помощью символа «;»:

Далее из палитры Инструменты графиков вызовем поле декартовых координат (Ctrl+2), где в позиции на оси абсцисс запишемP(ω), а на оси ординат –Q(ω):

Для построения вещественной и мнимойчастотных характеристик звена зададим диапазон и шаг изменения аргумента(частоты), воспользовавшись знаком «многоточие», вызываемым с помощью символа «;»:

 :=0, 0.1.. 1000

Далее из палитры Инструменты графиков вызовем поле декартовых координат (Ctrl+2), где в позиции на оси абсцисс запишем, а на оси ординат – P(ω) илиQ(ω):

Теперь определим амплитудную-частотную (АЧХ) и фазовую частотную (ФЧХ) характеристики. По определению, АЧХ вычисляется как модуль комплексного коэффициента передачи, а ФЧХ - как его аргумент:

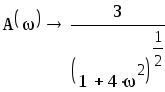
Действительная логарифмическая АЧХ в соответствии с определением вычисляется по формуле:

Д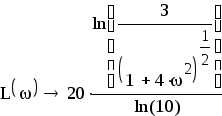ля построения логарифмических частотных характеристик из палитрыИнструменты графиков вызовем поле координат (Ctrl+2), где в позиции на оси ординат запишем логарифмическую АЧХ L() или фазовую частотную характеристику(), а на оси абсцисс задаем логарифмический масштаб -lg.

Далее произвести построение асимптотических логарифмических частотных характеристик системы автоматического регулирования по вариантам заданий 4-ой лабораторной работы в соответствии с методикой изложенной выше в п.4.2.4.

15