Работа № 5 Построение логарифмических частотных характеристик систем автоматического регулирования

Продолжительность работы – 4 часов.

Цель работы

Получение навыков расчета частотных характеристик элементарных линейных звеньев. Исследование особенностей построения частотных характеристик (вещественных, мнимых, амплитудно-частотных, фазовых) и реальных и идеальных (асимптотических) логарифмических частотных характеристик элементарных линейных звеньев, построение характеристик с применением пакета символьной математики Mathcad.

Теоретическое обоснование

При практических расчетах СУ удобно использовать частотные характеристики, построенные в логарифмических координатах. Такие характеристики называют логарифмическими.Они имеют наименьшую кривизну и могут быть приближенно заменены ломанными линиями, составленными из нескольких отрезков. Причем эти отрезки в большинстве случаев удается построить без громоздких вычислений, при помощи некоторых простых правил. Кроме того в логарифмической системе координат легко находятся характеристики различных соединительных элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.

Логарифмическая частотная характеристика (ЛАЧХ)– частотная характеристика в логарифмическом масштабе.

L(), дб Октава

20

10

-1 0 1 2 lg

0,1 0,5 1 2 5 10 100

-10 Декада

-20

За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервалы частоты, заключенный между произвольным значением ω_iи его десятикратным значением 10ω_i. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1.

Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ)

L(ω)=20lg{W(ω)}

Ординаты которой измеряют в логарифмических единицах – Белах или децибелах(дБ).

1 Бел = 10 дБ

1 Бел – единица измерения мощностей двух сигналов.

- ЛАЧХ

из передаточной функциисистемы заменой комплексной переменнойsнаможет быть получена функция, называемаякомплексным коэффициентом передачи системы

комплексный коэффициент передачи может быть представлен в двух видах:

,

,

где и -вещественная и мнимаячастотные характеристики системы,

и-амплитудно-частотнаяифазово-частотная характеристики системы.

Связь между этими частотными характеристиками определяется формулами

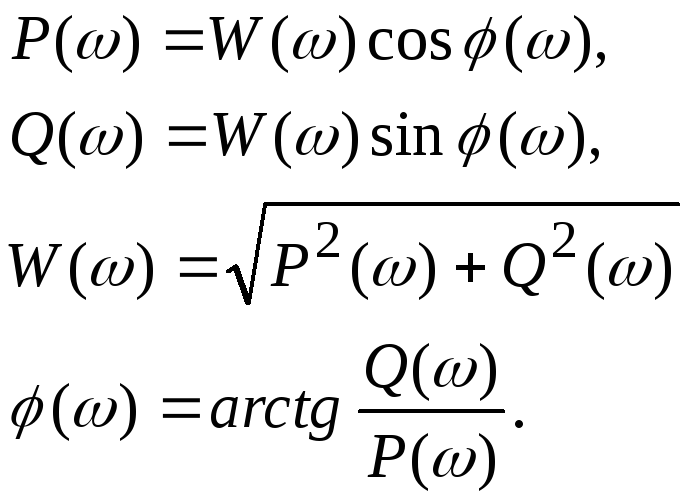
Амплитудно-частотная характеристика системы является модулем комплексного коэффициента передачи , а фазовая частотная характеристика - его аргументом

В частотной области динамические свойства линейных звеньев характеризуются амплитудно-частотной (АЧХ) и фазочастотной(ФЧХ) характеристиками. Эти характеристики связаны с передаточной функциейсоотношениями

где - комплексный коэффициент передачи,

- комплексная переменная

При анализе и синтезе систем управления используются логарифмические частотные характеристики (ЛАЧХ).

Функция называетсялогарифмической амплитудно-частотной характеристикой(ЛАЧХ). По оси абсцисс ЛАЧХ строится в десятичном масштабе частот, а по оси ординат -Единицей измеренияявляется децибел (дБ), а единицей измерения интервала частоты - декада. Декада - интервал частоты, на котором она изменяется в десять раз.

Логарифмической фазочастотной характеристикой (ЛФЧХ) называется фазовая частотная характеристика , построенная в десятичном масштабе частотlgω. Логарифмическая фазовая частотная характеристика (ЛФЧХ) измеряется в радианах или градусах.

Низкочастотная асимптота ЛАЧХ представляет собой предел

Высокочастотная асимптота ЛАЧХ есть предел логарифмической АЧХ

Асимптотической ЛАЧХ является характеристика, составленная из асимптот.

Разность между действительной и асимптотическойЛАЧХ есть поправка

Частота , на которой сопрягаются различные асимптоты, называются частотой сопряжения.

Для ЛАЧХ, составленных из трех и более участков асимптот, существует несколько частот сопряжения ω_с1, ω_с2, ω_с3, и т.д. Обычно частоты сопряжения нумеруются в порядке возрастания, т.е.ω_с1<ω_с2<ω_с3<…Наибольшая разностьимеет место на частоте спряженияω_сi.Поэтому именно в ее окрестностях следует учитывать поправку.

Построение логарифмических частотных характеристик сложных систем

• Методика построения ЛАЧХ сводится к следующим этапам:

• ЛАЧХ строится по W(s) разомкнутой части системы.

• Определить коэффициент пропорциональности системы К и 20lgК ;

• Определить частоты сопряжения элементарных звеньев и определить lgwс, гдеwс- соответствующие частоты сопряжения;

• Расположить элементарные звенья по возрастанию частот сопряжения wс и lgwс;

• Задаться наклоном +20дБ/дек или -20дБ/дек и кратным им наклонам в масштабе координатной плоскости;

• Если передаточная функция разомкнутой части системы содержит nодинаковых звеньев, то наклон ЛАЧХ будет увеличен вnраз.

Методику построения ЛАЧХ системы можно разделить на четыре типа по особенностям системы управления:

• для статической системы;

• для астатической;

• для системы с дифференцирующим звеном;

• для системы с неявно выраженным апериодическим звеном второго порядка.

Ниже представлены частотные характеристики и асимптотические ЛАЧХ и методика их расчета для типовых звеньев.