5.3.2. Метод корреляционного анализа

В различных исследованиях появляется необходимость определять связи между различными количественными или качественными показате­лями. Если какая-либо физическая величина определяется как однознач­ная функция одной или нескольких величин

то такая связь называется функциональной. Функциональная связь может существовать и между случайными величинами.

Но между случайными величинами может быть связь и другого ро­да. Она проявляется в том, что одна из случайных величин реагирует на изменения другой изменениями своего закона распределения. Такая связь называется стохастической (вероятностной), или статистической, обнару­живаемой лишь при массовом изучении признаков.

Стохастическая связь между случайными величинами появляется тогда, когда имеются общие случайные факторы, влияющие одновременно как на одну, так и на другую величину. Например, если

то величины х и у будут связаны между собой стохастически, что означает: каждому заданному значению x соответствует не одно определенное зна­чение у, а целое распределение у, которое изменяется с изменением х.

Стохастические связи могут быть очень сложными, но наиболее простым и имеющим важное практическое значение видом стохастической связи является корреляционная связь.

Корреляционная связь между двумя случайными переменными ве­личинами выражается в том, что на изменения одной случайной величины другая случайная величина реагирует изменениями своего среднего значе­ния или математического ожидания. Таким образом, понятие корреляци­онная связь - более узкое понятие, чем понятие стохастической связи, так как математическое ожидание является только одним из параметров рас­пределения и еще не определяет закона распределения в целом.

Метод корреляционного анализа состоит из обработки статистиче­ских данных, отражающих тесноту (силу) связи между стоимостью изде­лий и их показателями качества.

Метод корреляционного анализа применим для задач третьего типа (см. п. 5.2) и для тех изделий, для которых интегральный ПК является ос­новной характеристикой технико-экономической эффективности их ис­пользования. Поэтому при нормировании ПК такого типа изделий в состав НПКП следует включать показатели, которые оказывают существенное влияние на величину интегрального ПК, характеризующего отношение по­лезного суммарного эффекта от эксплуатации изделия к суммарным затра­там на его создание и эксплуатацию.

При использовании метода корреляционного анализа критерием принятия решения является коэффициент корреляции, а его значение -решающим правилом.

Определение НПКП производится путем установления связи между ценой изделия и ПК, которая в общем случае определяется силой связи че­рез корреляционное отношение :

,

где - среднеквадратическое отклонение фактических значений у_i- от среднего т.е.

;

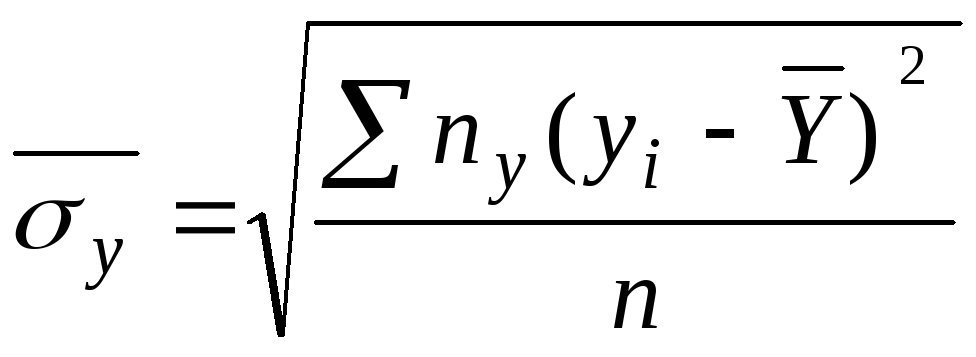- среднеквадратическое отклонение значений условного среднего (среднее арифметическое значение наблюдавшихся значений Y, соответствующих определенному значению X) от общего среднего ,т.е.

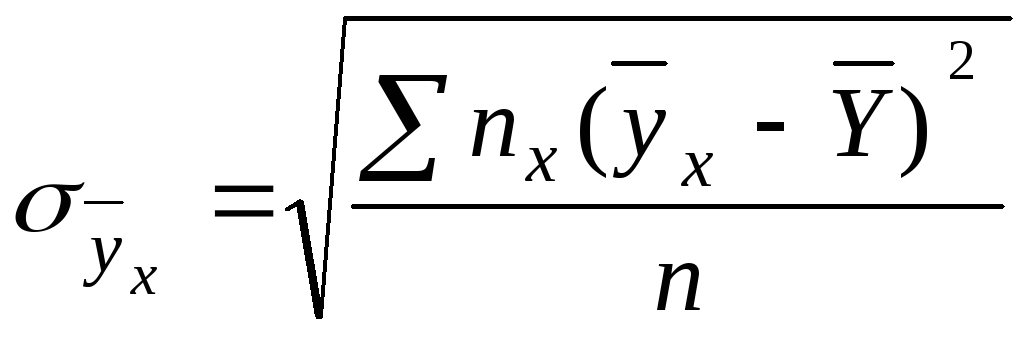
п - объем выборки (количество изделий);

п_у и п_х - частоты значений (количество появлений одного и того же значения за время контроля) случайных величин у и х, соот­ветственно.

Корреляционное отношение служит мерой тесноты связи любой формы; в том числе и линейной. В этом его преимущество в сравнении с коэффициентом корреляции , который оценивает силу связи только при линейной зависимости случайных величии и модуль которого равен корреляционному отношению [24]:

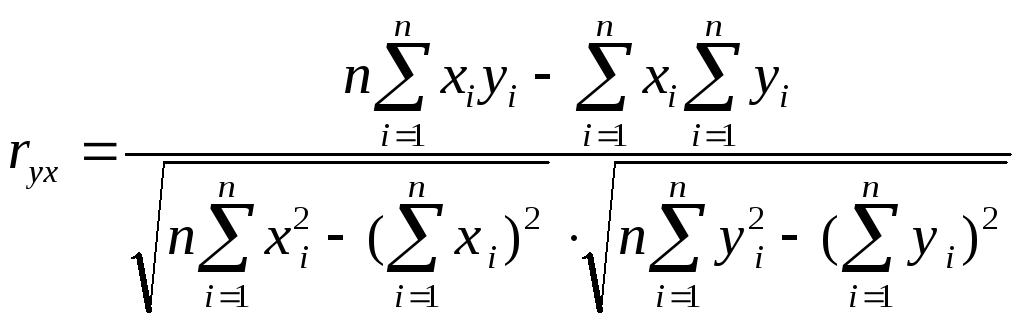, (5.1)

где п - количество изделий в выборке;

i - индекс (номер) изделия в выборке.

Анализ различной литературы, связанной с применением математи­ческой статистики в технологии машиностроения, показал, что при кон­троле по количественному признаку показатель качества имеет непрерыв­ное, нормальное распределение [24, с.113 и 25, с. 143]. В тоже время, если случайные величины распределены нормально, то они связаны линейной корреляционной зависимостью [26, с. 184]. Поэтому для определения НПКП достаточно воспользоваться коэффициентом корреляции.

При r_ух= ± 1 переменные х и у связаны прямолинейной связью. Если r_ух = 0, то между х и у не существует прямолинейная связь, а только криво­линейная (в связи с вышеизложенным не рассматривается). Чем ближе r_ух к единице, тем точнее и теснее прямолинейная корреляционная связь у с х и наоборот.

Если имеющихся статистических данных достаточно для определе­ния значимости влияния оцениваемых ПК x_j на величину интегрального ПК Y, то вычисляются коэффициенты корреляции между ПК x_j и состав­ляющими интегрального ПК Y: себестоимостью изготовления изделия (у₁), средней приведенной стоимостью эксплуатации изделия (у₂), годовой стоимостью эффекта от применения изделия (у₃) и др. По величине коэф­фициентов корреляции оценивается значимость влияния величины отдель­ного ПК на величину основных составляющих интегрального ПК. Вычис­ленные коэффициенты корреляции заносятся в таблицу:

Y	xj
			…
			…
			…
…
			…

После определения коэффициента корреляции для последующих расчетов оставляются те ПК, которые имеют наибольшее значение коэф­фициента корреляции. Остальные ПК исключаются с целью снижения временных затрат на проведение исследований, т.к. они незначительно влияют на цену изделия.

Для дальнейшего сокращения числа учитываемых ПК оценивается теснота связи между отдельными ПК, для чего рассчитываются коэффициенты парной корреляции между ПК.

Если значения коэффициентов парной корреляции по абсолютной величине достаточно велики (например, больше 0,8), то в НПКП включают показатель, который теснее связан с ценой, т.е. у которого коэффициент парной корреляции больше.

После отбора ПК указанными способами проводится статистическая проверка достоверности рассчитанных коэффициентов парной корреляции при ограниченной выборке изделий в сравнении с действительными.

Значимость коэффициента парной корреляции оценивается через построение доверительных интервалов с заданной доверительной вероят­ностью . (Если с заданной коэффициент корреляции равен нулю, то оцениваемый ПК не зависит от другого ПК).

Для определения доверительного интервала используется преобра­зование Фишера:

(5.2)

где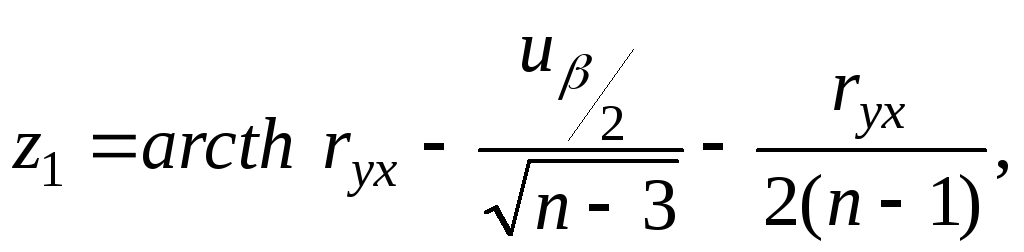

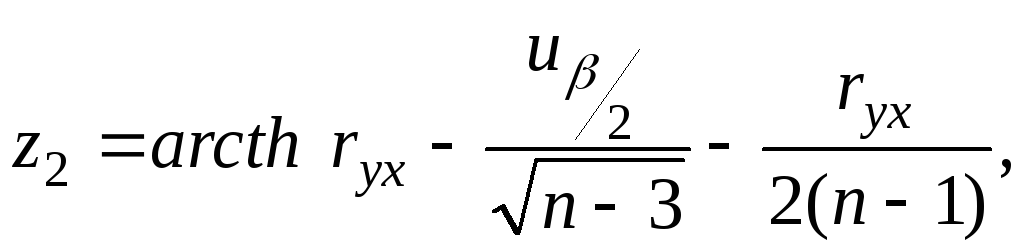
th z₁ - гиперболический тангенс, определяемый по табличным дан­ным преобразования Фишера;

- квантиль нормального распределения (обратное нормальное распределение при заданной вероятности для указанного среднего и стандартного отклонений).

За критерий целесообразности включения отдельных ПК в искомую НПКП принимается величина модуля коэффициента корреляции между случайными величинами у_l и x_j .

Решение этой задачи в математической статистике производится по­становкой и проверкой так называемой "нулевой гипотезы", под которой подразумевается допущение об отсутствии различия, в данном случае, между рассчитанной НПКП и истинной. Для проверки гипотез используются критерии, которые в математической статистике называются критериями согласия. Для того чтобы принять или забраковать гипотезу с помощью этих критериев, установлены их уровни значимости. Уровень значимости представляет собой достаточно малое значение вероятности, отвечающее событиям, которые в данном исследовании можно считать практически невозможными. Обычно принимаются пяти-, двух- или однопроцентный уровень значимости [24, с. 73].

Уровень значимости называется также доверительным уровнем ве­роятности, который может быть принят равным Р = 0,05; 0,01 или 0,001. Эти уровни соответствуют классификации явлений на редкие (0,05), очень редкие (0,01) и чрезвычайно редкие (0,001). Выбирая тот или иной довери­тельный уровень вероятности, можно установить и область допустимых его значений, которая выражается вероятностью . Для практиче­ских целей достаточно принять [27, с. 13].

В результате таких оценок все ПК, удовлетворяющие условию

, обозначаются знаком "+"; неудовлетворяющие - знаком "-". По­лученная таблица имеет вид:

Y	xj
			…
	+	+	…	
…
	+	+	…	

В состав НПКП включаются те ПК, которым соответствует знак "+".

Выше были определены необходимые условия для определения контролируемых параметров.

Достаточность решения данной задачи оценивается по критерию множественной корреляции (регрессии) R, вычисляемому по каждому из показателей качества и характеризующему их совместное влияние на стоимость продукции, причем . КоэффициентR одновременно служит и ограничением числа учитываемых ПК. Практически, начиная с некоторого значения, дальнейшее увеличение числа ПК не приводит к рос­ту коэффициента множественной регрессии, однако при этом заметно воз­растают трудозатраты на проведение различных видов испытаний. Считается, что условие достаточности обеспечено, если [27, с. 151]:

(5.3)

m – количество ПК в НПКП.

Пример. Определить ПК компрессора типа ГП для включения в НПКП при оценке их влияния на стоимость Y компрессоров на основе исходных данных, полученных из за­водской отчетности (табл. 5.4) из следующего состава [28]:

• производительность ;

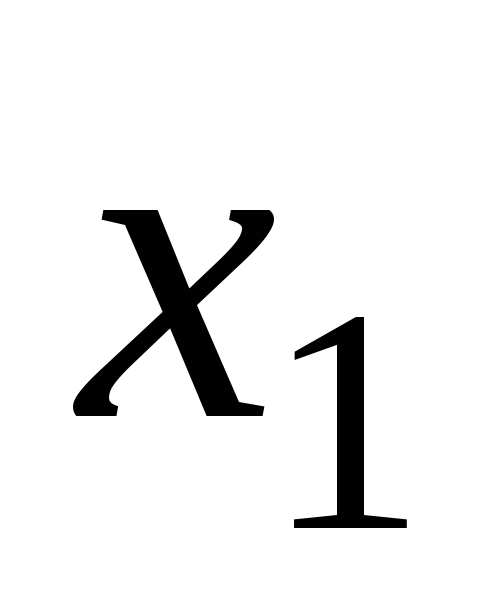• давления нагнетания ;

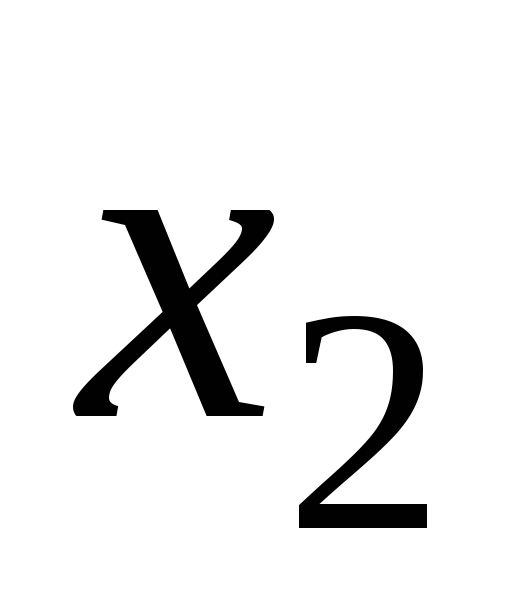• число оборотов ;

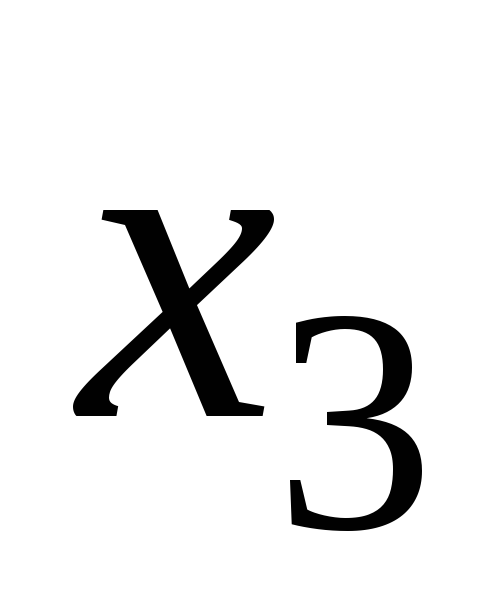• мощность на валу ;

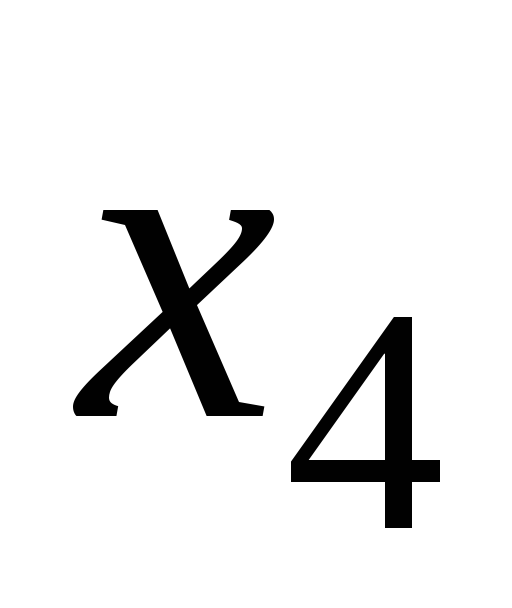• вес .

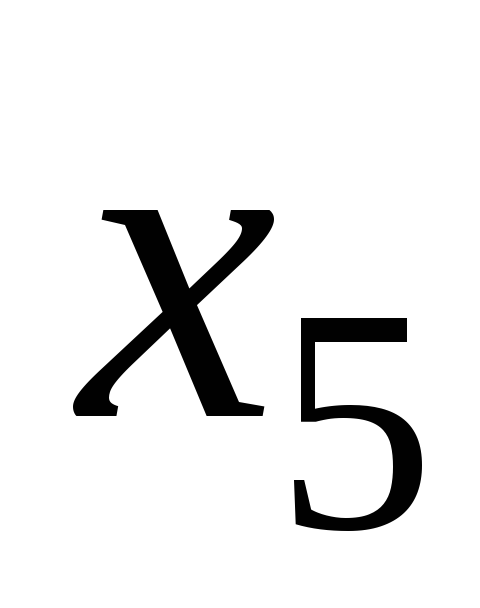Таблица 5.4