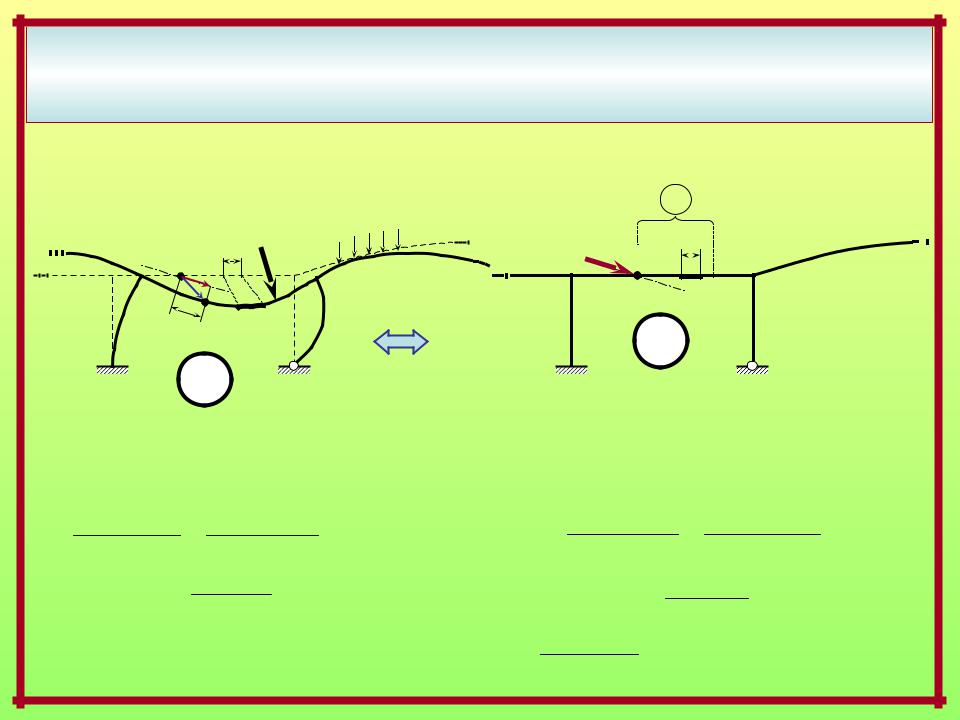
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
|
Выражения возможных работ внешних и внутренних сил через внутренние |
|||||||||||||||||||||||||
|
силовые факторы в стержневых системах с прямолинейными элементами |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
и стержнями малой кривизны |
|
j |
|
|
|
|
Вспомогательное |
|||||||||
|
|
Действительное состояние – силовое |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
i |
В |
|
|
ds F |
|
q |
|
Fi = 1 |
В |
|
dsj |
|
единичное состояние |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
В1 |
|
|
Wint,iF = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
iF |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
F |
|
|
|
Элемент ds j– му элементу /участку (ds dsj ) |
||||||||||||||||
|
Обобщение на случай |
|
системы, имеющей m |
элементов/участков, |
||||||||||||||||||||||
пространственного сложного |
тогда для всей системы: |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
dWext,iF j |
|||||
|
сопротивления стержня: |
|
Wint,iF |
Wext,iF |
|
|||||||||||||||||||||
|
|
dWint,iF dWext,iF |
|
|
m |
|
|
|
|
|
|
j 1 |
|
|
|
|||||||||||
|
Mz,i Mz,F |
|
My,i My,F |
|
Mz,i Mz,F |
|
M y,i M y,F |
|
||||||||||||||||||
|
||||||||||||||||||||||||||
|
EIz |
|
|
|
EIy |
|
EIz |
|
|
|
|
EI y |
|
|||||||||||||
|
|
|
|
|
|
|
|
j 1 l j |
|
|
|
|
|
|
|
|
|
|||||||||
|
Mt,i Mt,F |
|
|
Ni NF |
|
|
|
Mt,i Mt,F |
|
N |
i |
N |
F |
|
|
|||||||||||
|
GIt |
|
|
EA |
|
|
GIt |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EA |
|
|
|
|||||||||
kτy |
Qy,i Qy,F |
kτz |
Q Q |
ds |
kτy |
Q |
|
Q |
|
kτz |
Q Q |
dsj |
||||||||||||||
|
|
z,i |
z,F |
|
y,i |
|
y,F |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
GA |
|
|
|
|
|
GA |
|
|
|
|
|
|
|
|
|
|
|
|
z,i |
z,F |
|
|||
|
|
|
|
|
|
|
|
|
|
GA |
|
|
|
|
|
|
|
GA |
|
|
||||||
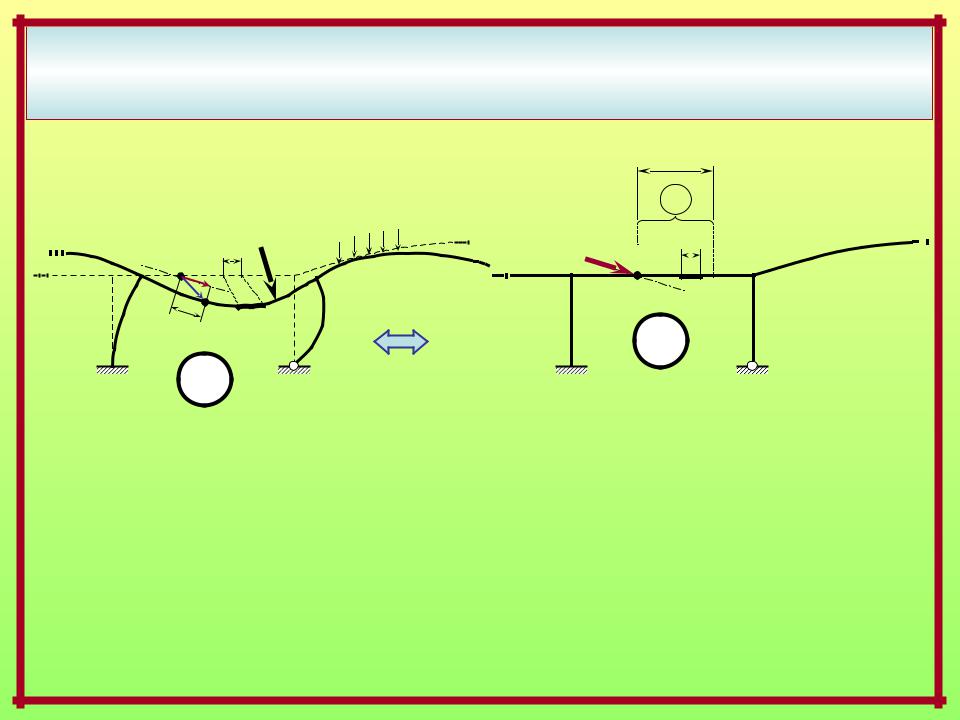
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
ПО МЕТОДУ МАКСВЕЛЛА – МОРА
По базовой формуле ММ–М:
|
|
|
|
|
iF =– Wint,iF |
Действительное состояние – силовое |
|||||
i |
В |
|
ds F |
q |
Fi = 1 |
|
|
|
|
||
|
|
|
В1 |
iF |
Wint,iF = ? |
|
i |
|
|||
|
|
F |
|
||
F
|
lj |
|
|
j |
Вспомогательное |
|
ds |
единичное состояние |
В |
|
j |
i |
|
|
|
|
i
|
|
|
|
|
|
|
m |
|
Mz,i Mz,F |
|
My,i |
mMy,F |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
iF Wint,iF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
EI |
z |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
j |
|
||||||||||||
|
|
Wext,iF |
|
EI |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
Wint,iF |
|
|
|
|
|
dWext,iF |
||||||||||||||||||||||||||||
|
M |
|
M |
|
|
|
j 1 l j |
|
Q m Q |
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
t,i |
t,F |
|
Ni NF |
|
|
y,F |
|
|
|
|
|
Q |
|
|
|
Q |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
kτy |
|
|
kτz |
|
|
|
|
|
|
|
|
|
|
|
dsj |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Mz,i Mz,F |
z,iM y,i |
|
M y,F |
|
|||||||||||||||||||||
|
|
GI |
|
|
EA |
|
|
|
GA |
|
|
|
|
z |
|
|
|
|
GA |
|
|
|
y |
|
|
|
|
|||||||||
|
|
|
t |
|
|
|
|
|
|
j 1 l j |
|
|
|
EI |
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Mt,i Mt,F |
|
N |
|
N |
F |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
GIt |
|
|
|
|
|
EA |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Qy,i Qy,F |
|
|
|
|
|
Qz,i Qz,F |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
kτy |
|
|
|
|
|
|
|
|
kτz |
|
|
|
|
|
|
|
|
|
|
|
dsj |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
GA |
|
|
|
|
|
GA |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
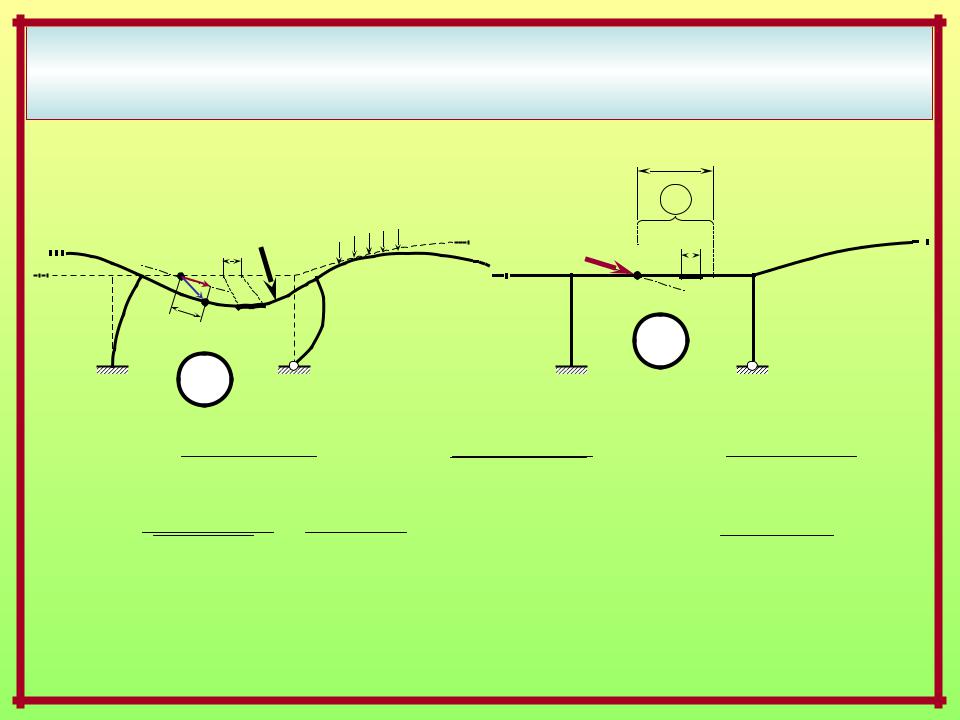
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
ПО МЕТОДУ МАКСВЕЛЛА – МОРА
По базовой формуле ММ–М:
iF =– Wint,iF |
lj |
Действительное состояние – силовое |
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
Вспомогательное |
|||||||||||||||||||||||||||||||||||
|
|
|
i |
|
В |
|
|
ds F |
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
Fi = 1 |
|
В |
dsj |
|
единичное состояние |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
В1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
Вариант записи формулы Максвелла – Мора |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
для перемещения от силовых воздействий: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
mM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
M |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
M M |
|
|
|
|
|
m M y |
|
My,i My,F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M M M |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
z,i |
|
|
|
|
|
|
|
|
|
|
|
z,i |
|
|
|
z,F |
|
ds |
|
y,i |
|
Mt |
|
|
|
|
|
|
t,F |
ds |
|
|
||||||||||||||
iF |
|
iF |
Wint,iF |
j |
|
|
|
|
EIy |
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|||||||||||||||||||||||
|
|
j 1 |
|
|
|
|
EIz |
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
GIt |
|
|
|
|
|
|
||||||||||||||
|
|
l j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
l j |
|
|
|
|
z |
|
|
|
|
|
|
|
j |
1 y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
j 1 l j |
|
Q Q |
|
|
|
mQz Q |
l j |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
mN M |
t,i |
t,F |
|
|
|
|
mQz |
|
|
|
|
|
Q |
|
|
|
|
|
Q |
|
Q |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
N |
N |
|
|
|
|
|
Q |
|
|
|
y,F |
|
|
|
|
|
|
z,i |
Q |
|
|
|
|
|
|
|
|
|||||||||||||
|
Ni |
NF |
|
|
|
i |
|
|
F |
|
ky,i |
|
y,i |
|
|
k |
|
|
|
|
|
z,F |
|
z,dsF |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
y,F |
ds |
|
|
k |
|
z,i |
|
|
jds |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ds |
j |
|
|
k |
|
|
|
τy |
|
|
|
|
j |
|
|
|
τz |
|
|
|
|
|
|
|
|
j |
|
|
||||||||||||||
|
GI |
|
|
|
|
|
|
|
|
τy |
|
|
|
|
GA |
|
|
|
|
|
τz |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
EA |
|
|
|
|
GA |
|
|
|
|
|
|
GA |
GA |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
j 1 l j |
|
|
|
EAt |
|
|
|
|
|
|
|
j 1 l j |
|
|
|
|
|
|
|
|
|
|
|
|
j 1 l j |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
В общем случае все величины в подынтегральном выражении – функции |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
координаты сечения sj |
|
( для прямолинейного стержня – xj |
): |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
Mz,i = Mz,i |
(sj ), |
|
Mz,F = Mz,F |
(sj) ,…, NF |
= NF (sj ), …, |
Qz,F = Qz,F (sj ) , |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
EIz = EIz (sj) ,…, GIt = GIt (sj ) , EA = EA(sj ) , GA = GA(sj ) ,…, k z = k z (sj ) |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
ПО МЕТОДУ МАКСВЕЛЛА – МОРА
По базовой формуле ММ–М:
iF =– Wint,iF |
lj |
Действительное состояние – силовое |
|
|
|
|
|
|
|
j |
|
|
Вспомогательное |
|||||||||||||||||||||
|
|
|
i |
|
В |
|
ds F |
|
q |
|
|
|
|
|
|
|
Fi = 1 |
В |
|
dsj |
единичное состояние |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
В1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
Вариант записи формулы Максвелла – Мора |
|
|
|
|
|
|
|
|||||||||||||||||
|
mMz |
|
|
|
для перемещения от силовых воздействий: |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
EI |
|
|
|
|
|
mM y |
|
EI |
|
|
|
|
mMt |
|
|
GI |
|
|
|
|
|
||||||||
iF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
Mz,i |
Mz,F dsj |
|
My,i |
My,F dsj |
|
|
|
Mt,i |
Mt,F dsj |
|||||||||||||||||||
|
|
|
j 1 l j |
|
|
|
z |
Изгиб |
|
|
j 1 l j |
|
|
y |
Изгиб |
m |
|
j 1 l j |
|
|
|
|
t |
Кручение |
|
|||||||
mN |
|
|
N N |
|
|
|
mQ |
|
|
|
Qy,i Qy,F |
|
|
|
|
Qz,i Qz,F |
|
|
|
|||||||||||||
|
|
|
|
|
|
y |
|
|
|
Qz |
|
|
|
|
|
|||||||||||||||||
EAi |
F dsj kτy |
|
GA |
|
|
dsj kτz |
|
|
GA |
|
|
dsj |
|
|||||||||||||||||||
j 1 l j |
Растяжение/сжатие |
j 1 |
l j |
Сдвиг |
|
|
|
|
j 1 l j |
Сдвиг |
|
|
u |
|
Rj,i Rj,F |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Учёт деформируемых ( нежёстких ) упругоподатливых связей в системе: |
|
|
|
|
c |
j |
|
|||||||||||||||||||||||||
Rj |
|
|
|
|
|
Rj |
|
|
|
|
|
|
|
Закон Гука для |
|
|
|
|
|
j 1 |
|
|
|
|||||||||
c |
|
|
|
|
|
|
|
c |
|
|
|
c |
|
|
упругих связей: |
|
|
u – суммарное число |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Rj = cj * j |
|
|
|
|
|||||||||||||||
|
|
Жёсткости линейных и угловых упругих связей |
|
|
|
|
|
|
внешних и |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
внутренних |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
упругих связей |
|
|||||
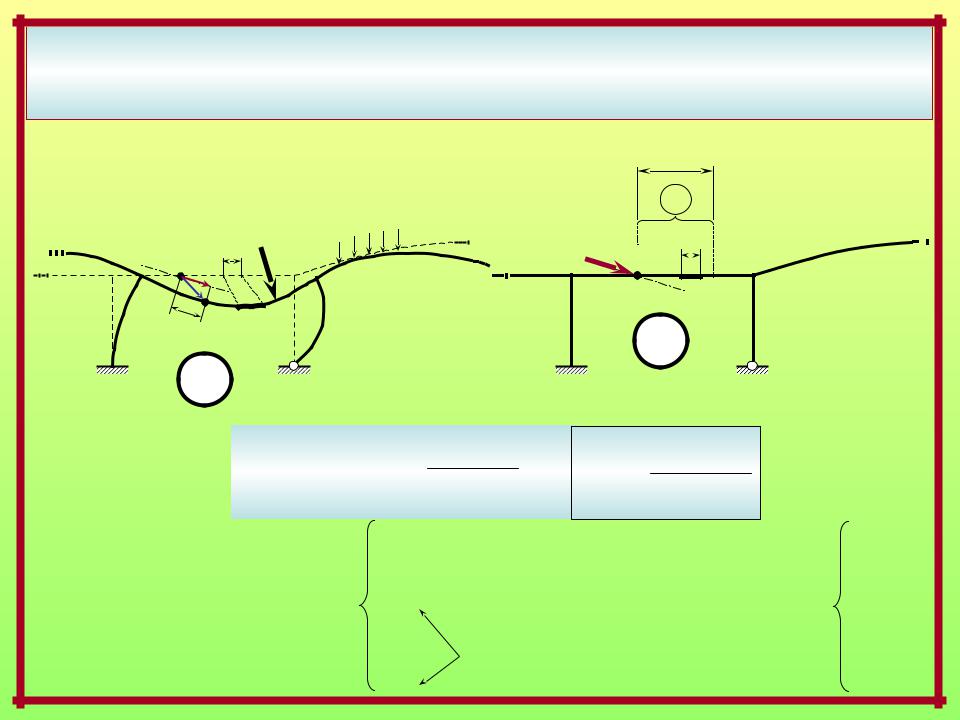
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
ПО МЕТОДУ МАКСВЕЛЛА – МОРА
По базовой формуле ММ–М:
iF =– Wint,iF |
lj |
Действительное состояние – силовое |
|
|
j |
|
|
Вспомогательное |
|||||||||
i |
В |
|
|
ds F |
q |
|
|
Fi = 1 |
В |
|
dsj |
единичное состояние |
|||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|||
|
|
|
В1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
Краткая запись формулы Максвелла – Мора |
|
|||||||||||
|
|
|
|
для перемещения от силовых воздействий: |
|
||||||||||
|
|
|
|
|
|
mS |
S S |
u |
R |
|
R |
|
|
||
|
|
|
|
iF iC |
F dsj |
|
|
j,i |
|
|
j,F |
|
|||
|
|
|
|
|
по S j 1 l j |
|
S |
j 1 |
|
cj |
|
|
|
||
|
|
|
|
|
|
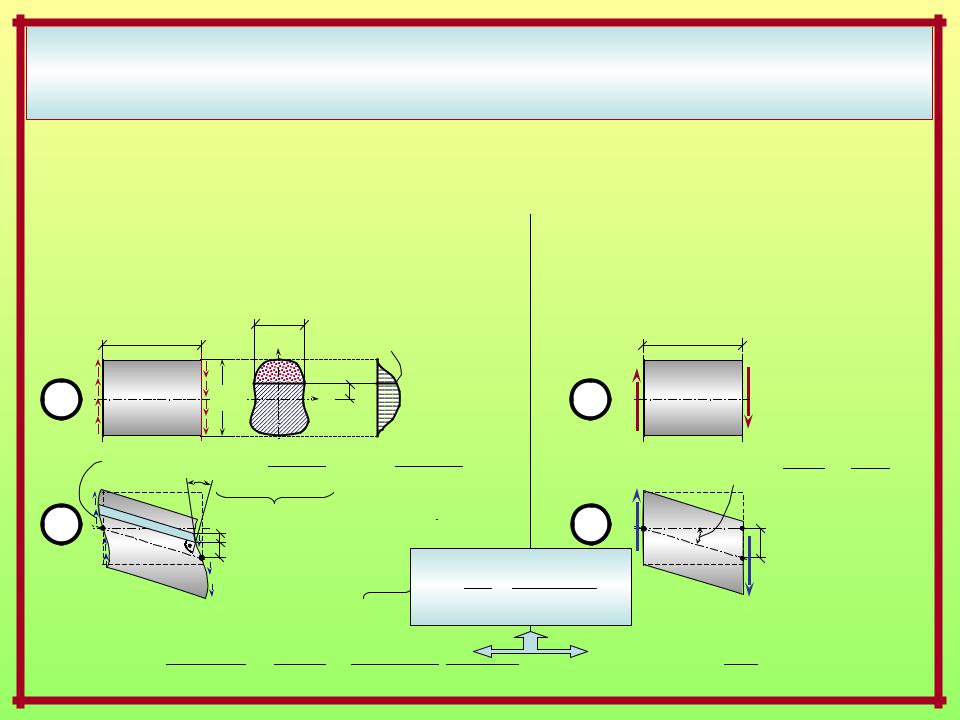
Mz,… |
C – обобщённое обозначение |
EIz |
|||||||
S… – обобщённое обозначение |
My,… |
S |
жёсткости сечения при |
EIy |
|||||||||||
внутреннего силового |
Mt,… |
|
деформации, соответству- |
GIt |
|||||||||||
фактора: |
|
|
S… |
N… |
|
ющей силовому фактору S: CS |
EA |
||||||||
|
|
|
|
|
|
i F |
|
|
|
|
|
|
|||
|
|
|
|
|
|
Qy,… |
|
|
|
|
|
|
GA/k y |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Qz,… |
|
|
|
|
|
|
|
|
GA/k z |
|
|
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ВОЗДЕЙСТВИЙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
ПО МЕТОДУ МАКСВЕЛЛА – МОРА |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
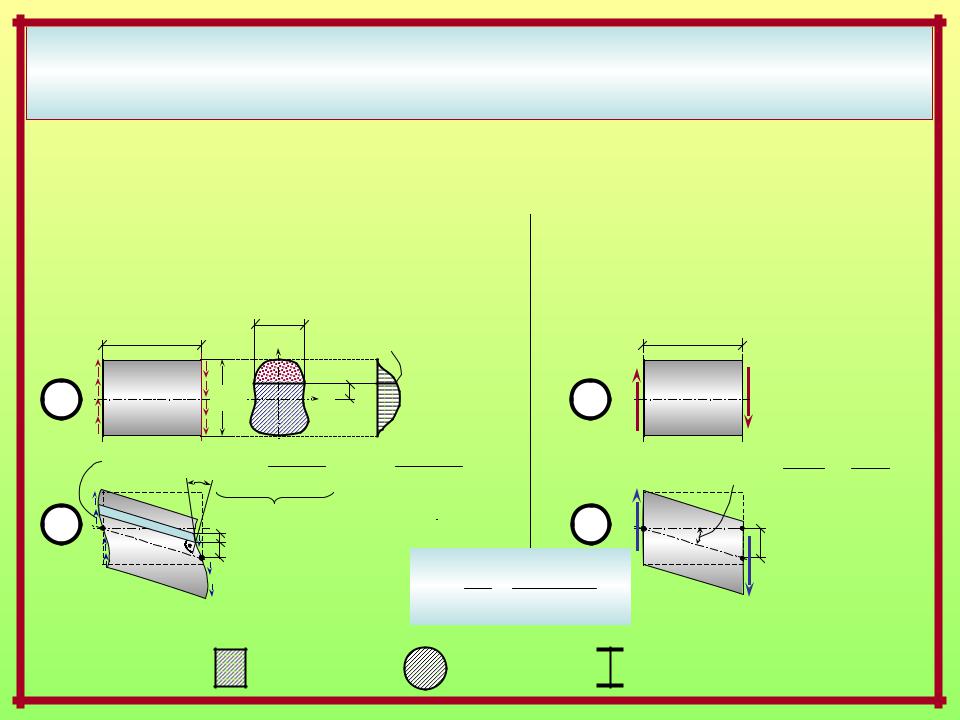
К вопросу об учёте деформации сдвига при определении перемещений |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1. Формула для коэффициента k |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Формула выводится путём сопоставления выражений возможных |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
работ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
по двум расчётным моделям элемента ds: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
а) с фактическими касательными напряжениями |
|
б) с обобщёнными силами ( поперечными |
||||||||||||||||||||||||||||||||
i (y) |
в концевых сечениях элемента ds |
во вспо- |
|
силами Qi ) в концевых сечениях эле- |
||||||||||||||||||||||||||||||
могательном i-ом единичном состоянии и |
фак- |
|
мента ds в i-ом единичном состоянии |
|||||||||||||||||||||||||||||||
тическими |
деформациями сдвига F (y) в дейст- |
|
и соответствующими |
обобщёнными |
|
|||||||||||||||||||||||||||||
вительном состоянии: |
b(y) |
|
|
τi (y) |
Q S (y) |
перемещениями |
( абсолютным сдвигом |
|||||||||||||||||||||||||||
|
|
|
ds |
|
|
|
|
|
|
i |
z |
|
dvF ) в действительном состоянии: |
|
||||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
b(y) Iz |
|
|
|
Qi |
|
ds |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
h |
|
|
z |
|
|
y |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
Qi τ |
|
|
|
|||
|
|
F (y) |
γF (y) |
τF (y) |
|
Q |
|
|
S (y) |
|
|
|
|
|
|
|
|
γ |
|
0,F |
Q |
k |
||||||||||||
|
|
|
|
|
F |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
QF |
|
|
|
|
|
G |
F |
||||||||||||
|
|
|
|
|
|
|
|
|
G b(y) Iz |
|
|
|
|
|
|
|
|
|
0,F |
|
|
GA |
τ |
|||||||||||
F |
|
|
|
dy |
|
По закону |
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Гука |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dvF = 0,F * ds |
|||||||||
|
|
|
|
y |
|
при сдвигеdV |
|
A |
|
Sz (y) |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
QF |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
b(y) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
( a ) |
|
|
|
|
|
|
|
|
τ |
|
|
I2 |
|
dWext,iF( б ) Qi dvF |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qi γ0,F ds |
|||||||||||||||||
|
|
|
dWext,iF τi (y) γF (y) b(y) ds dy |
z |
h |
|
|
|||||||||||||||||||||||||||
|
Q S (y) |
h |
|
|
|
|
|
S (y) |
2 |
|
S |
|
|
|
|
|
|
|
Q Q |
|
|
|
|
|
|
|
|
|||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
( б ) |
|
|
|
|
|
|
|
|
||||||||||||
|
Q S y |
|
Qi QF |
|
|
|
|
|
|
|
|
|
|
|
i |
|
F |
|
|
|
|
|
|
|
||||||||||
|
i |
z |
|
F z ( ) |
|
|
Qi QzF |
|
|
z |
|
|
|
|
dW |
|
QF |
|
|
|
|
|
|
|||||||||||
ds |
|
|
|
dWext,iF b(y) dy ds |
|
|
|
ds dy |
|
|
|
|
|
|
|
|
|
|
k ds |
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
ext,iF Q |
|
|
|
|
τk ds |
|
|
||||||||||||||||
b(y) I |
|
Gb(y) I |
|
|
2 |
|
|
|
|
|
b( |
|
|
|
|
|
|
i |
|
|
|
|
|
τ |
|
|
|
|
||||||
z |
z |
|
GIz |
|
b(y) |
|
|
|
|
|
|
GA |
|
|
|
|
|
|
|
|||||||||||||||
h |
|
|
|
|
|
|
hGIz |
|
h |
|
|
|
|
|
|
|
|
|
GA |
|
|
|
|
|
||||||||||
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ |
|
|
|||||||||||||||||
|
|
|
|
|
ВОЗДЕЙСТВИЙ |
|
|
|
|
|
|
|
|
||||||
|
ПО МЕТОДУ МАКСВЕЛЛА – МОРА |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
Приложение |
|
|
|
|
|
|
|
|
|
|||
К вопросу об учёте деформации сдвига при определении перемещений |
|||||||||||||||||||
|
|
|
1. Формула для коэффициента k |
|
|
|
|
|
|
||||||||||
Формула выводится путем сопоставления выражений возможных |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
работ |
|
|
|
|
|
|
|
|
|
|
|
|
|
по двум расчётным моделям элемента ds: |
|
|
|
|
|
|
|||||||||||
а) с фактическими касательными напряжениями |
|
б) с обобщёнными силами ( поперечными |
|||||||||||||||||
i (y) в концевых сечениях элемента ds |
во вспо- |
|
силами Qi ) в концевых сечениях эле- |
||||||||||||||||
могательном i-ом единичном состоянии и фак- |
|
мента ds |
в i-ом единичном состоянии |
||||||||||||||||
тическими деформациями сдвига F (y) в дейст- |
|
и соответствующими обобщёнными |
|
||||||||||||||||
вительном состоянии: ёb(y) |
|
τi (y) Qi Sz(y) |
перемещениями ( абсолютным сдвигом |
||||||||||||||||
|
dvF ) в действительном состоянии: |
|
|||||||||||||||||
ds |
|
|
y |
|
|
|
|
b(y) Iz |
|
|
Qi |
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
h |
|
z |
|
y |
|
|
|
|
|
i |
|
|
Qi τ |
|
|
|
||
F (y) |
γF (y) |
τF (y) |
|
Q |
|
S (y) |
|
|
|
|
γ |
0,F |
Q |
k |
|||||
|
|
F |
|
z |
|
|
|
|
|
|
|
|
|||||||
G |
|
|
|
|
|
|
QF |
|
G |
F |
|||||||||
|
|
|
|
G b(y) Iz |
|
|
|
|
0,F |
|
GA |
τ |
|||||||
F |
dy |
|
По закону |
|
|
|
F |
|
|
|
|
|
|
|
|
||||
|
|
Гука |
|
|
|
|
|
|
|
|
|
dvF = 0,F * ds |
|||||||
|
y |
|
при сдвиге |
k A |
|
Sz (y) |
2 |
|
|
|
|||||||||
|
|
|
|
dy |
|
|
QF |
|
|
|
|
||||||||
|
|
|
|
|
|
|
τ |
Iz2 |
h |
b(y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Значения коэффициента k для некоторых видов сечений: |
|
|
|
|
|
|||||||||||||
|
|
k = 6/5 |
|
|
|
|
k = 10/9 |
|
k A/Aw |
|
|
|
|
|
|
||||
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
ПО МЕТОДУ МАКСВЕЛЛА – МОРА
Приложение
К вопросу об учёте деформации сдвига при определении перемещений
2. Оценка влияния сдвига на перемещения от силовых воздействий
Составляющая перемещения iF , обусловленная деформацией сдвига, – iF,Q ; в отношении к составляющей iF,M от изгиба: iF,Q / iF,M = Q
|
|
Для j-го участка/элемента постоянного сечения: |
|
|
|
||||||||||
|
|
( j) |
|
Ej |
( j) |
|
( j) 2 |
hj 2 |
( j) |
|
|
|
|
|
|
|
|
αQ |
|
|
kτ |
|
αr |
|
βS |
, |
|
|
2 |
Qi QF dsj |
|
|
|
Gj |
|
|
|||||||||||
где α( j) r / h |
|
|
|
|
|
lj |
|
|
|
|
lj |
||||
< 0,5 – относительный радиус инерции сечения; |
( j) |
|
|
lj |
|||||||||||
r |
j j |
|
|
|
|
|
|
|
|
|
βS |
|
|
|
|
|
|
|
|
|
|
|
|
|
Mi MF dsj |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Признаки необходимости учёта деформации сдвига |
|
|
lj |
|
|||||||||
|
|
при определении перемещений стержневых систем: |
|
|
|
|
|||||||||
|
сечение – тонкостенное ( k |
> 2 ); |
|
|
|
|
|
|
|
|
|
||||
материал – относительно низкомодульный при сдвиге ( E/G > 3…4 );элемент достаточно массивный, «короткий» ( h/l > 1/8 );
нагрузки таковы, что вызывают значительные поперечные силы
при сравнительно небольших изгибающих моментах
( ориентировочно: средние на грузовом участке | M/Q | < ~ h ).
Подробнее см.: Себешев В.Г. Особенности работы статически неопределимых систем и регулирование усилий в конструкциях: учебное пособие. – Новосибирск: НГАСУ (Сибстрин), 2009. – 164 с.
К о н т р о л ь н ы е в о п р о с
ы
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы; для перехода к слайду с ответом можно сделать щелчок мышью по номеру в
скобках*); для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 29» )
1. Как в общем виде обозначаются перемещения? Какой смысл имеют индексы в этом обозначении? ( 2 )
2. Что такое собственное перемещение? ( 2 )
3. Какие индексы используются для обозначения перемещений от силовых, температурных, кинематических и комбинированных воздействий? ( 3 )
4. Какие перемещения называются единичными? ( 4 )
4. Какова основная идея метода Максвелла – Мора определения перемещений деформируемых систем? Почему этот метод также называется методом единичных вспомогательных нагрузок? ( 5 )
5. Правило задания вспомогательного единичного воздействия. Каков кинематический смысл этого воздействия? ( 6 )
6. Типовые случаи вспомогательных единичных состояний в методе Максвелла – Мора. ( 7 )
7. Какой принцип механики лежит в основе метода Максвелла – Мора? ( 8 )
8. Через какие величины выражается искомое перемещение по базовой формуле метода Максвелла – Мора? ( 8 )
9. Что такое возможная работа внешних или внутренних сил? ( 9 )
10. Какая работа внешних или внутренних сил называется действительной? ( 9 ) 11. Что называется потенциальной энергией деформации системы? ( 9 )
12. Как связаны возможные работы внешних и внутренних сил ( 10 ) , их действительные работы и потенциальная энергия упругой деформации (ПЭУД)? ( 12 )
_____________________________________________________
*) Только в режиме «Показ слайдов»
К о н т р о л ь н ы е в о п р о с
ы
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы; для перехода к слайду с ответом можно сделать щелчок мышью по номеру в
скобках*); для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 30» )
13. Как выражаются возможные и действительные работы внешних и внутренних сил и ПЭУД через обобщённые нагрузки и обобщённые перемещения? Частный случай – линейно деформируемые системы ( теорема Клапейрона ). ( 10 – 12 )
14. Какой приём используется для получения выражения возможной работы через внутренние силовые факторы? ( 16 )
15. Как деформации действительного силового состояния выражаются через внутренние силовые факторы? ( 18 )
16. Каков смысл величин EI, EA, GIt , GA/k , входящих в формулу Максвелла – Мора? ( 18 )
17. Варианты развёрнутой записи формулы Максвелла – Мора для перемещения от силовых воздействий. ( 22, 23 )
18. Какими слагаемыми в формуле Максвелла – Мора учитываются разные виды упругих деформаций элементов ( изгиб, растяжение/сжатие, сдвиг, кручение )? ( 24 )
19. Что учитывает коэффициент k в слагаемом формулы Максвелла – Мора, отражающем
влияние сдвига? ( 18 ) ( 27 )
20.Как учитываются в формуле Максвелла – Мора деформации упругоподатливых связей системы? ( 24 )
21.Краткая обобщённая запись формулы Максвелла – Мора для перемещения от силового воздействия. ( 25 )
22.Какие величины обобщённо обозначаются как Si и SF в краткой записи формулы Максвелла – Мора? То же, СS? ( 25 )
_____________________________________________________
*) Только в режиме «Показ слайдов»