
- •СТРОИТЕЛЬНАЯ МЕХАНИКА.
- •МЕТОД МАКСВЕЛЛА – МОРА
- •МЕТОД МАКСВЕЛЛА – МОРА
- •МЕТОД МАКСВЕЛЛА – МОРА
- •МЕТОД МАКСВЕЛЛА – МОРА
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
- •ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
- •ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
- •ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
- •ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
- •ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ
- •ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
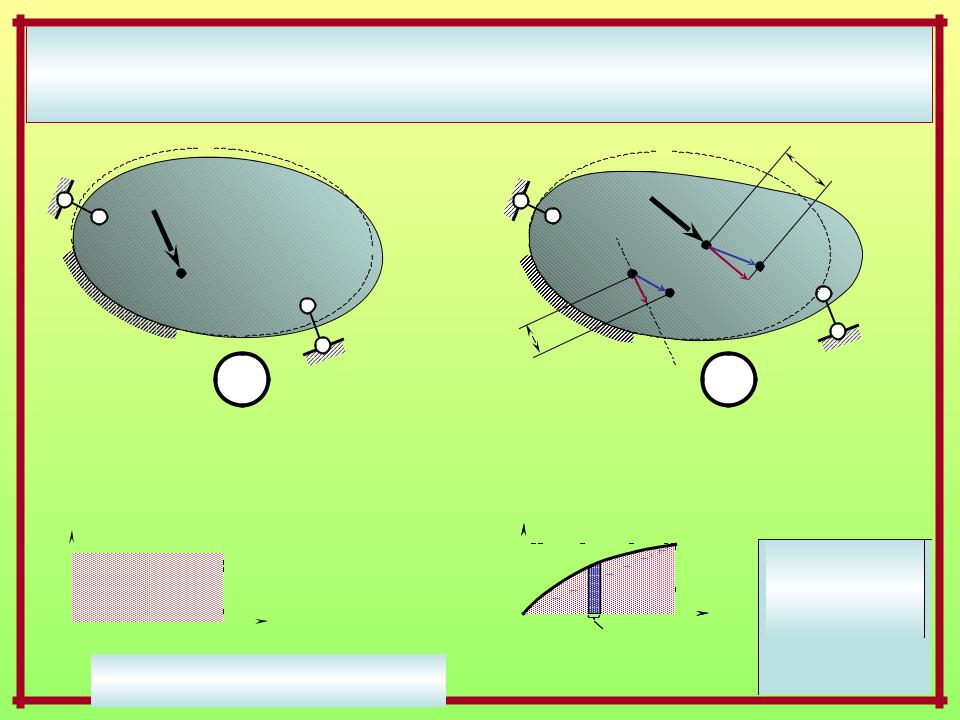
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Fi |
|
Fk |
|
kk |
|
|
|
||
A |
|
A |
B |
B1 |
|
|
|
A1 |
|
|
ik |
|
|
|
i |
i |
|
k |
|
|
|
|
|
Возможные работы внешних |
|
kk – собственное перемещение |
|||||||||||||||||||||||||||||||||||||||||||
и внутренних сил i –го состояния |
|
ik – |
|
побочное перемещение |
|
|
|
||||||||||||||||||||||||||||||||||||||||
на перемещениях k –го состояния: |
|
Fk |
|
|
|
|
|
|
|
|
|
|
|
|
|
Действительная работа |
|||||||||||||||||||||||||||||||
Fi |
|
Wext,ik |
= –Wint,ik |
|
|
Для ЛДС |
|
|
внешних сил |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Fk |
|
|
|
|
|
|
|
|
|
k |
–го состояния: |
|
||||||||||||||||||||||||||||
Fi |
|
|
|
|
ik= inv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
WW |
U |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
Fk( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kk |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
F |
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ext,ext,kk |
kk |
|
|
|
||||||
|
|
|
|
|
(F ) |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 F |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
kk |
|
|
|||
|
|
|
|
|
|
i |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (ζ)dζ |
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2k |
|
|
|
|
||
|
|
ik |
|
ik |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
kk |
|
kk |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1/2 |
Теорема0Клапейрона |
|
|||||||||||||||||||||||||
|
|
|
Wext, ik = –Wint, ik = Fi* ik U – ПЭУД |
|
|
|
|
|
η Fk |
kk |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( B.P.E. |
|
Clapeyron, 1834 ) |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
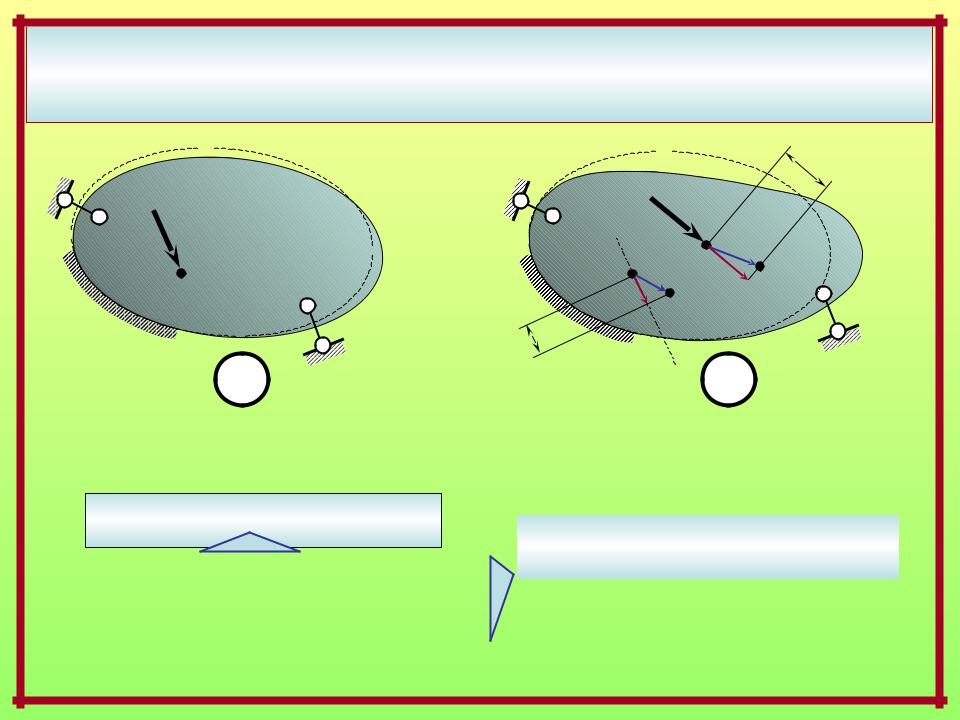
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Fi |
A |
i
|
Fk |
|
kk |
|
|
|
|
|
A |
B |
B1 |
|
|
A1 |
|
ik |
|
|
|
i |
|
k |
|
|
|
Возможные работы внешних и внутренних сил i –го состояния
на перемещениях k –го состояния:
Wext, ik = –Wint, ik = Fi* ik
Выражения возможных и действительных работ внешних и внутренних сил и ПЭУД через внешние силовые факторы
и перемещения (через обобщённые нагрузки
и обобщённые перемещения ).
Действительная работа внешних и внутренних сил k –го состояния, потенциальная энергия упругой деформации (ПЭУД) ЛДС:
W |
U W |
1 F |
ext,kk |
int,kk |
2 k kk |
Теорема Клапейрона
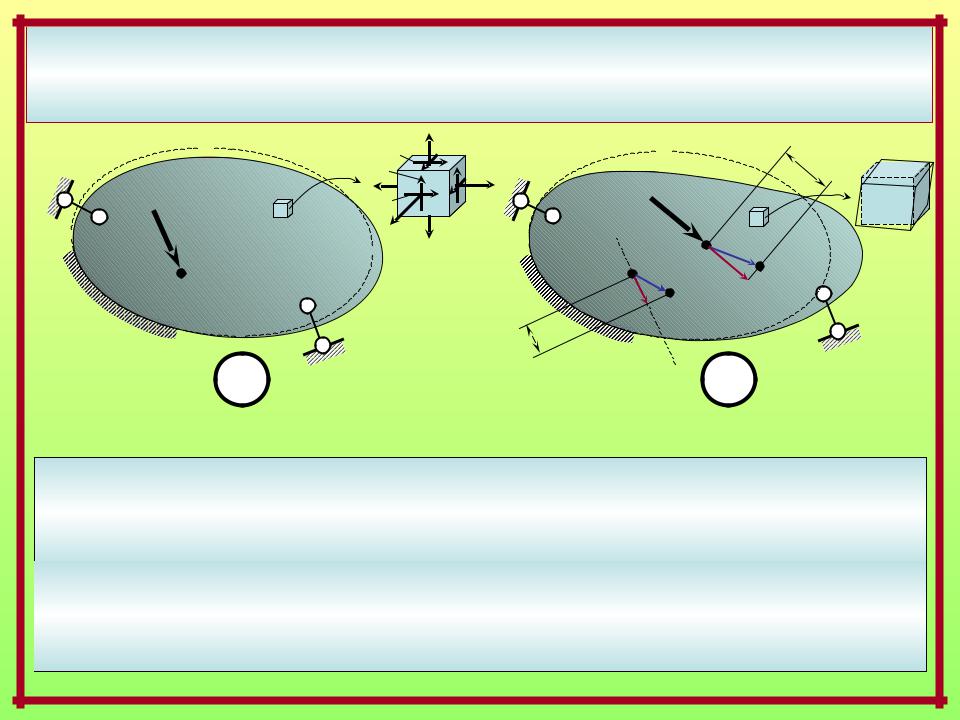
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
|
|
|
xy,i |
y,i |
F |
|
|
yz,i |
|
i |
dydx dz |
xz,i |
|
|
|
z,i |
|
||
|
|
|
||
|
|
A |
|
|
|
|
i |
|
|
x,i |
Fk |
|
kk |
|
|
|
|
|
A B |
|
x,k |
|
B1 |
|
|
|
z,ky,k |
||
|
A |
|
xy,k |
ik |
1 |
|
|
i |
k |
zx,kyz,k |
|
|
|
Выражения возможных и действительных работ внешних и внутренних сил и ПЭУД через внутренние силовые факторы ( напряжения) и деформации
|
Wext, ik Wint, ik |
|
|
|
σx,i εx,k σy,i εy,k σz,i εz,k τxy,i γxy,k τyz,i γyz,k τzx,i γzx,k dV |
V |
|
|
|
2 |
Wext, kk Wint, kk U |
|
|
1 |
σx,k εx,k σy,k εy,k σz,k εz,k τxy,k γxy,k τyz,k γyz,k τzx,k γzx,k dV |
V |
dV dx dy dz |
|

ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных и действительных работ внешних и внутренних сил и ПЭУД через внутренние силовые факторы ( напряжения) и деформации
|
|
Wext, ik Wint, ik |
|
|
|
|
|
σx,i εx,k σy,i εy,k σz,i εz,k τxy,i γxy,k τyz,i γyz,k τzx,i γzx,k dV |
|
V |
|
|
|
|
2 |
Wext, kk Wint, kk U |
|
|
||
1 |
σx,k εx,k σy,k εy,k σz,k εz,k τxy,k γxy,k τyz,k γyz,k τzx,k γzx,k dV |
|
|
|
V |
Физические зависимости, связывающие деформации k –го состояния с напряжениями |
||||||||
(для линейно деформируемого изотропного тела, с учётом температурной составляющей ) |
||||||||
εx,k |
σx,k |
ν σy,k σz,k / E α t ; ; εz,k σz,k ν σx,k σy,k / E α t ; |
||||||
|
|
|
γxy,k τxy,k |
/ G ; ; γzx,k τzx,k / G ; G E / 2 1 ν |
||||
|
|
|
|
|
Wext, ik |
Wint, ik |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Wext, kk U Wint, kk |
|
|
||
|
|
|
2 2 |
1 |
σx,i2 σx,k |
σy,i σy,k σz,i σz,k |
|
|
|
1 1 |
[σx,k σV y,kE σz,k 2ν |
σx,k σy,k σy,k σz,k |
σz,k σx,k |
|
|||
|
|
2 V Eν σx,i2σy,k 2σz,k σ2 y,i σz,k σx,k σz,i σx,k |
σy,k |
|
||||
|
2(1 ν) τzx,k τzx,k τzx,k Eα t σx,k σy,k |
σz,k ]dV |
|
|||||
2 |
(1 |
ν) τxy,i τxy,k τyz,i τyz,k |
τzx,i τzx,k Eα t σx,i σy,i σz,i |
}dV |
||||
|
|
|
|
|||||
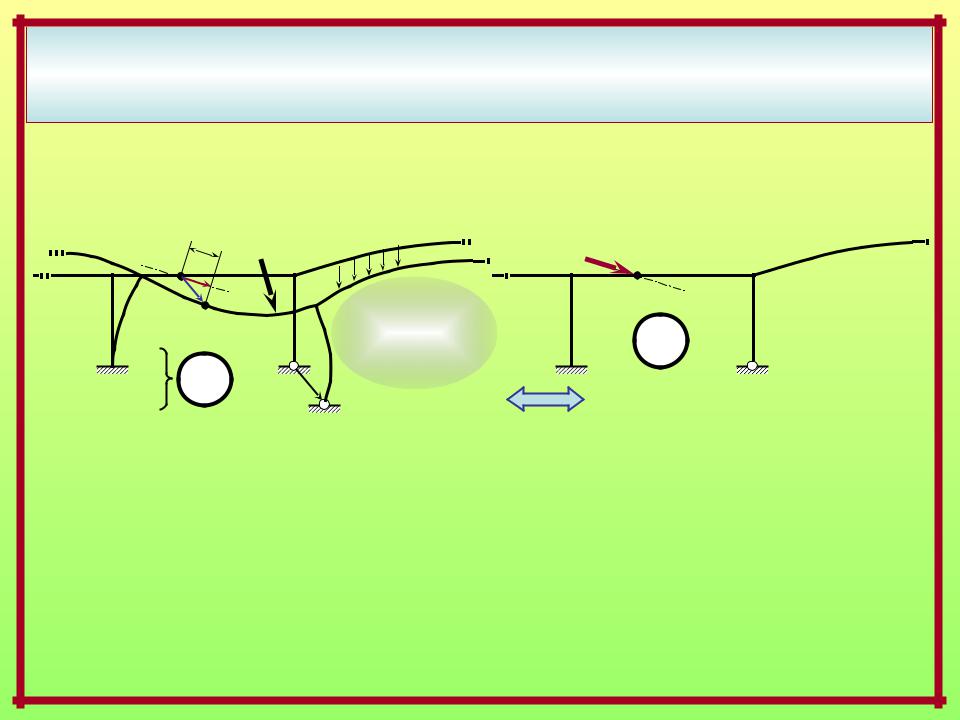
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
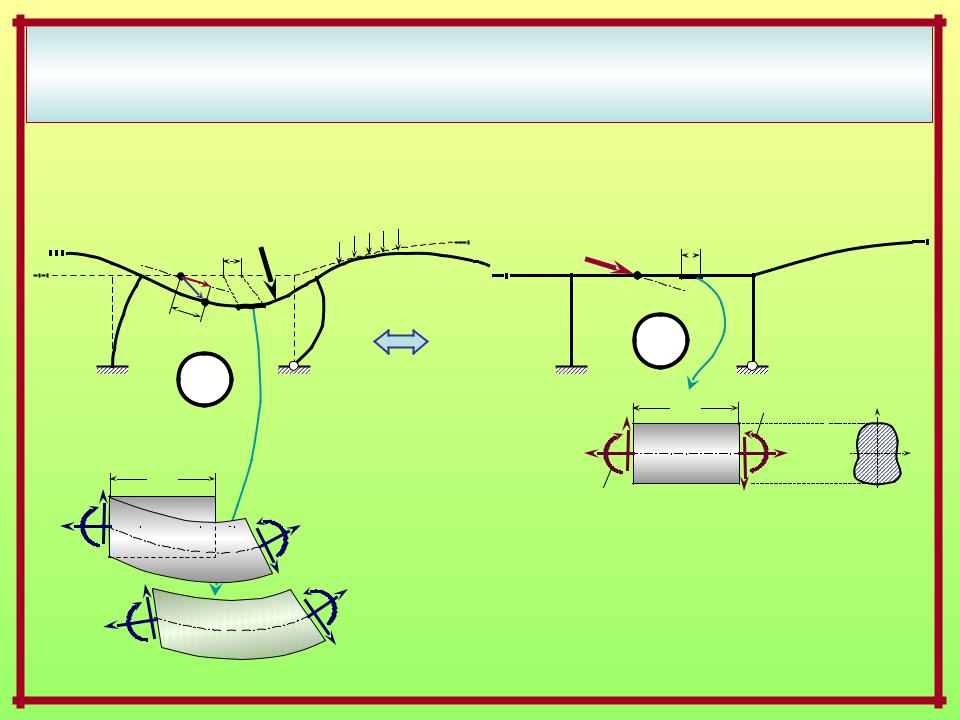
Выражения возможных работ внешних и внутренних сил через внутренние |
||||||||
силовые факторы в стержневых системах с прямолинейными элементами |
||||||||
|
|
|
|
|
и стержнями малой кривизны |
|||
|
|
|
|
|
|
|
Вспомогательное единичное состояние |
|
|
|
|
F |
|
|
Fi = 1 |
|
|
|
|
i |
|
|
|
|||
i |
В |
|
|
|
|
|
|
В |
|
|
|
q |
|
|
|||
|
|
|
|
|
|
|
i |
|
|
|
В1 |
|
|
|
|
||
|
|
|
t |
o |
|
i |
||
F |
|
|
|
|
|
|||
ct |
|
( j) |
|
i |
Wint,i = ? |
|||
В случае ЛДС i = iF + it + ic
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через внутренние силовые факторы в стержневых системах с прямолинейными элементами и стержнями малой кривизны
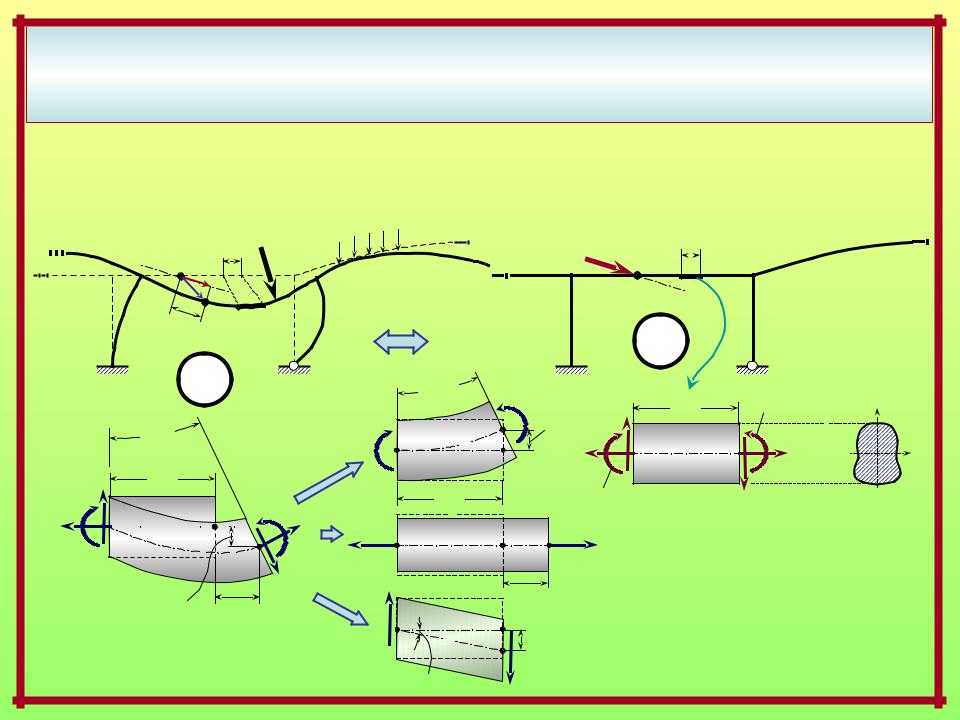
Действительное состояние – силовое Вспомогательное единичное состояние
i |
В |
|
ds F |
q |
|
|
|
|
|
||
|
|
|
В1 |
iF |
Wint,iF |
|
i |
|
|||
|
|
F |
|
||
F
QF |
ds |
MF +… |
|
|
NF |
|
|
||
|
NF |
+… |
||
MF QF |
||||
QF +…NF +… |
||||
NF |
MF |
|
MF +… |
|
|
|
QF +… |
||
Fi = 1 |
В |
ds |
|
i |
|
|
|
= ? i
Qi ds |
Mi + dMi |
y |
|
||
Ni |
Ni |
z |
Mi (Mz,i ) |
Qi (Qy,i ) |
|
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через внутренние силовые факторы в стержневых системах с прямолинейными элементами и стержнями малой кривизны
Действительное состояние – силовое Вспомогательное единичное состояние
i |
В |
|
ds F |
|
|
q |
|
Fi = 1 |
В |
ds |
|
|
||
|
|
|
|
|
|
|
|
|
i |
|
|
|||
|
|
|
В1 |
|
|
|
Wint,iF = ? |
|
|
|
|
|
||
|
|
|
|
iF |
|
|
|
i |
|
|
||||
|
i |
|
|
|
|
|
|
|
|
|||||
|
|
F |
|
|
|
|
|
|
|
|
|
|||
|
|
F |
|
|
MF |
d F |
MF |
|
Qi |
|
ds |
Mi + dMi |
y |
|
|
|
|
|
|
|
Изгиб |
~0 |
|
|
|
|
|
||
|
d F |
|
|
|
|
|
|
Ni |
|
|
Ni |
z |
||
QF |
ds |
|
|
|
|
|
|
|
|
|
||||
|
MF |
|
|
ds |
|
|
Mi |
(Mz,i ) |
Qi (Qy,i ) |
|
||||
NF |
|
|
|
NF |
|
|
|
|||||||
|
|
|
|
|
Растяжение |
|
|
Для i-го равновесного |
|
|||||
MF |
|
|
|
|
NF |
( сжатие ) |
|
NF |
|
|||||
|
|
|
QF |
|
|
|
состояния элемента ds |
|
||||||
|
dvF |
dsF |
F |
|
dsF |
|
линейно деформируемой системы: |
|||||||
|
|
|
|
|
|
Сдвиг |
dvF |
|
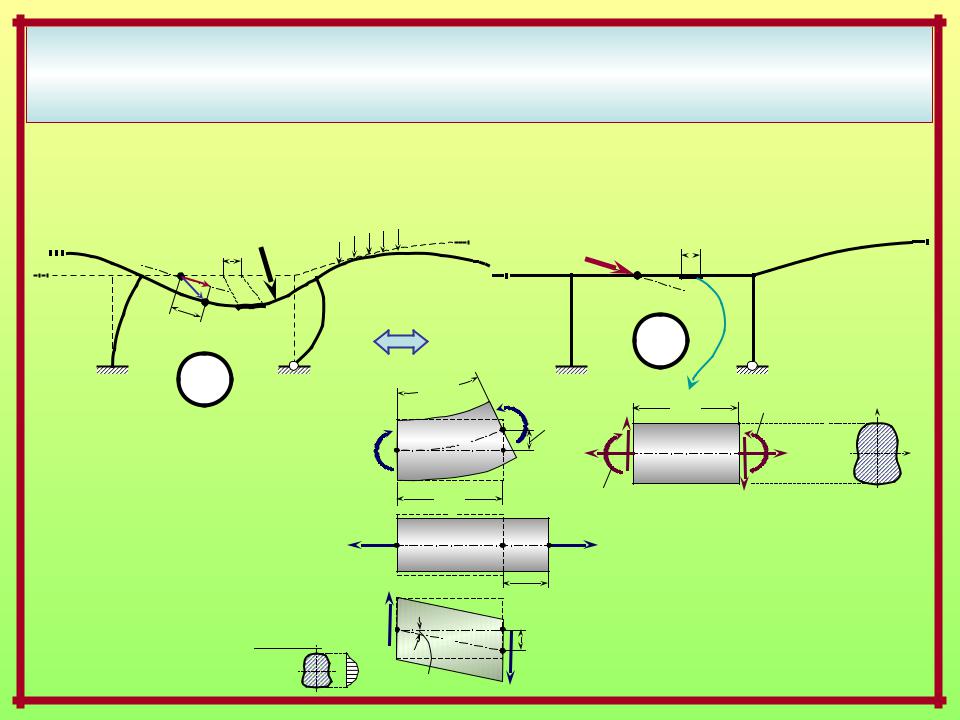
dWint,iF = – dWext,iF = |
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0,F |
QF |
|
=– |
(dWM,iF+dWN,iF +dWQ,iF ) |
|||
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через внутренние силовые факторы в стержневых системах с прямолинейными элементами и стержнями малой кривизны
Действительное состояние – силовое Вспомогательное единичное состояние
|
|
|
|
|
i |
|
В |
|
|
ds F |
|
|
q |
|
|
Fi = 1 |
В |
|
ds |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
В1 |
|
|
|
|
|
|
|
|
Wint,iF = ? |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iF |
|
|
i |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
MF |
d F |
MF |
Qi |
|
ds |
|
Mi + dMi |
y |
|
|||||
dWM, iF = Mi * d F = Mi * F |
* ds |
Изгиб |
~0 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
N |
|
|
|
z |
|||||||||||||||||||||
dWM,iF |
M |
* dθF |
|
Mi |
MF |
ds |
|
N |
i |
|
|
|
|
|
i |
|
|
|||||||||||||||
|
|
* |
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
N, iF |
= N |
i ds |
F |
= N |
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
i |
|
|
|
|
|
i EIF |
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
dWQ, iF = Qi * dvF = Qi * 0,F * ds |
NF |
|
Mi |
(Mz,i ) |
|
Qi (Qy,i ) |
|
|
||||||||||||||||||||||||
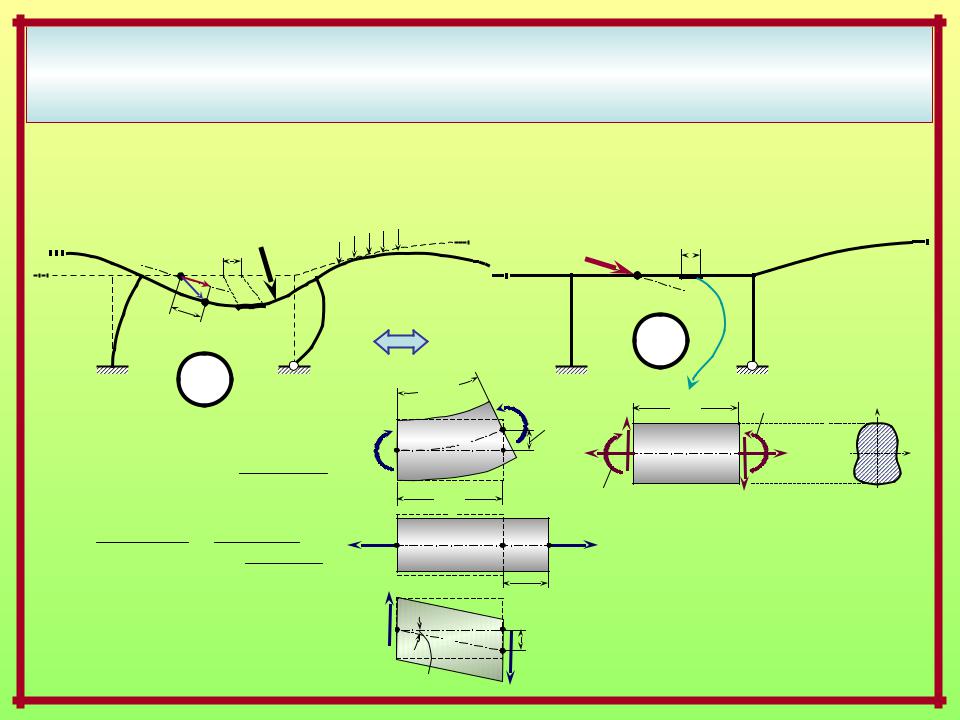
По закону Гука при изгибе, растяже- |
Растяжение |
|
Для i-го равновесного |
|
|
|||||||||||||||||||||||||||
|
( сжатие ) |
|
|
|
|
|||||||||||||||||||||||||||
dWN,iF |
Ni dsF |
Ni |
NF |
ds |
|
NF |
|
|
||||||||||||||||||||||||
нии (сжатии) и сдвиге соответственно: |
|
|
состояния элемента ds |
|
|
|||||||||||||||||||||||||||
F = MF /EI; |
|
|
|
|
|
|
EA |
|
|
|
|
|
|
|
||||||||||||||||||
F = NF |
/ EA; QF |
|
dsF |
линейно деформируемой системы: |
||||||||||||||||||||||||||||
|
0,F |
= |
|
0,F |
|
|
|
|
|
* |
QFi QF |
|
|
Сдвиг |
|
|
dW = – dW = |
|
||||||||||||||
|
|
|
/G = (k |
Q |
/A)/G |
|
dvF |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
dWQ,iF |
Qi |
dvF |
kτ |
|
GA |
|
ds |
|
|
=– |
(dW |
int,iF |
|
|
|
ext,iF |
|
) |
||||||||||||||
|
распределения касательных |
|
|
|
|
|
|
+dW |
|
+dW |
|
|||||||||||||||||||||
k |
|
– коэффициент неравномерности |
|
|
|
|
0,F |
QF |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
напряжений по сечению |
|
|
|
|
|
|
|
|
|
|
|
M,iF |
|
|
N,iF |
|
|
Q,iF |
|
|||||||||||
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через внутренние силовые факторы в стержневых системах с прямолинейными элементами и стержнями малой кривизны
Действительное состояние – силовое Вспомогательное единичное состояние
|
i |
|
В |
|
|
ds F |
|
q |
|
|
Fi = 1 |
В |
ds |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|||
|
|
|
|
|
В1 |
|
|
|
|
|
|
|
Wint,iF = ? |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
iF |
|
|
|
i |
|
|
|
|||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
F |
|
|
|
|
|
|
MF |
d F |
MF |
Qi |
|
ds |
Mi + dMi |
y |
|||
|
|
|
|
|
|
|
Mi |
MF |
Изгиб |
~0 |
|
|
|
|
|
z |
|||||
dWM,iF |
Mi dθF |
|
ds |
|
|
N |
i |
|
|
N |
i |
||||||||||
|
|
EI |
|
|
|
|
|
|
|
|
|||||||||||
dWint,iF |
dWext,iF |
|
|
|
|
ds |
|
Mi |
(Mz,i ) |
Qi (Qy,i ) |
|
||||||||||
Mi MF |
|
|
Ni |
NF |
|
NF |
|
|
|||||||||||||
|
|
Растяжение |
|
|
|
|
|
|
|||||||||||||
|
EI |
|
|
|
Ni |
NF |
|
|
|
|
|
|
|
||||||||
dW |
ds |
|
EA |
|
|
ds |
|
( сжатие ) |
|
|
Для i-го равновесного |
|
|||||||||
N |
|
|
|
|
EA |
|
|
NF |
|
||||||||||||
N,iF |
iQi QFF |
|
|
|
Q |
|
|
состояния элемента ds |
|
||||||||||||
|
kτ |
|
GA |
|
ds |
|
|
|
F |
|
dsF |
линейно деформируемой системы: |
|||||||||
|
|
|
|
|
|
Qi |
QF |
|
|
|
|||||||||||
dWQ,iF Qi dvF |
kτ |
|
ds |
|
Сдвиг |
dvF |
|
dWint,iF = – dWext,iF |
= |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
GA |
|
|
0,F |
=– |
(dWM,iF+dWN,iF +dWQ,iF ) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
QF |
|||||||
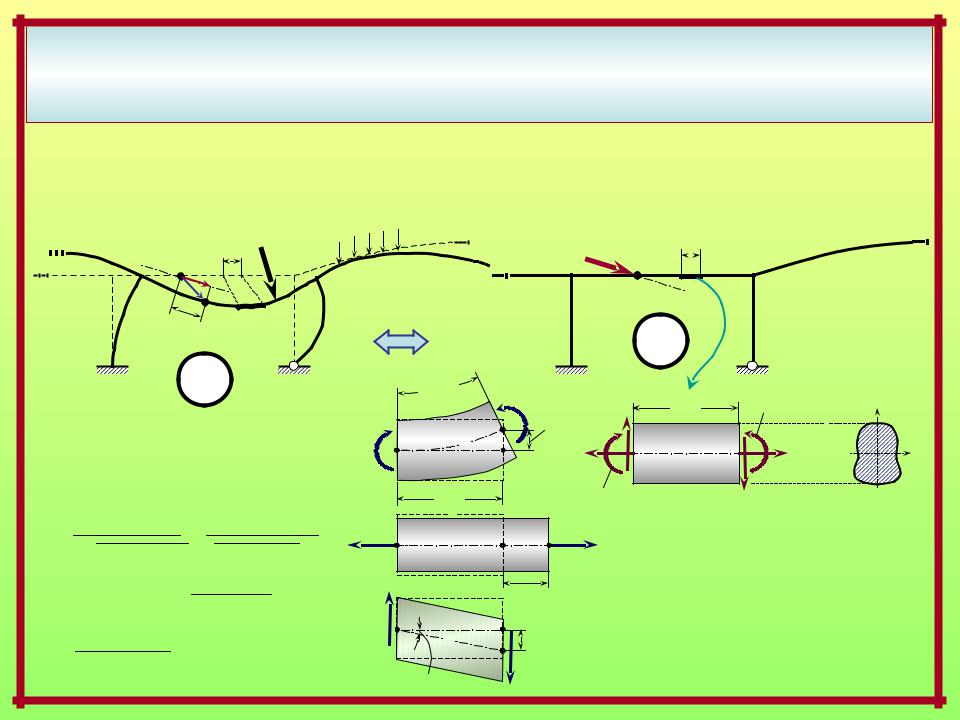
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через внутренние силовые факторы в стержневых системах с прямолинейными элементами и стержнями малой кривизны
Действительное состояние – силовое Вспомогательное единичное состояние
|
|
|
|
|
i |
|
В |
|
|
|
|
ds F |
|
|
|
|
q |
|
|
|
Fi = 1 |
В |
ds |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
В1 |
|
|
|
|
|
|
|
|
Wint,iF = ? |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iF |
|
|
|
|
i |
|
|
||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
MF |
d F |
MF |
|
|
Qi |
|
ds |
Mi + dMi |
y |
|||
|
Обобщение на случай |
|
|
Изгиб |
~0 |
|
|
|
|
|
||||||||||||||||||||||
пространственного сложного |
|
|
|
|
Ni |
|
|
Ni |
z |
|||||||||||||||||||||||
|
сопротивления стержня: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
dWint,iF |
dWext,iF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
dWint,iF |
|
|
|
|
|
ext,iF |
|
|
|
|
|
ds |
|
|
|
Mi |
(Mz,i ) |
Qi (Qy,i ) |
|
|||||||||||
|
|
M |
z,i |
M |
z,F |
|
|
M |
y,i |
M |
y,F |
|
N |
|
|
|
|
|
||||||||||||||
|
Mi |
MF |
|
Ni |
NF |
|
|
|
Растяжение |
|
|
|
|
|
|
|
||||||||||||||||
|
|
EI |
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
( сжатие ) |
|
|
|
|
Для i-го равновесного |
|
||||||||||||||
|
|
|
|
EI |
|
|
|
|
|
|
|
|
EA |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
NF |
|
|
|
|
|
|
Mt,i Mt,F |
|
|
|
|
Ni |
NF |
|
|
|
|
|
|
|
|
|
состояния элемента ds |
|
||||||||||||||
|
|
|
|
|
|
Qi QF |
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
kτ |
|
|
|
|
|
|
ds |
|
|
|
F |
|
ds |
|
|
линейно деформируемой системы: |
||||||||||||||
|
|
GI |
|
|
|
|
GA |
|
EA |
|
|
|
|
|
|
F |
|
|||||||||||||||
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сдвиг |
|
|
|
dWint,iF = – dWext,iF = |
|||||||||
|
|
Qy,i Qy,F |
|
|
|
|
|
|
Qz,i Qz,F |
|
dvF |
|
||||||||||||||||||||
kτy |
|
GA |
|
|
kτz |
|
|
GA |
|
|
ds |
|
|
=–(dWM,iF+dWN,iF +dWQ,iF ) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,F |
QF |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
