ГСХ Литература / ГСХ первый проект / ЖБК

Это окончание работы конструкции по упругой

q

статической схеме (рис. III.12.1). При дальнейшем

увеличении нагрузки (2-й этап) в опорных сечени-

S′

S

S′

ях арматура S′ продолжает течь, опорные момен-

ты не растут (M′ = –q1l 2 /12 = const), зато растут

l

моменты в пролете, пока при некоторй нагрузк q2

l2 /12=

l2 /16

не достигнут предельного значения: M

=q

l 2 /12 (íå-

1-é ýòàï

2

1

2

сущая способность пролетного и опорных сечений

1

–q =–q

/24

l2 /8

в нашем случае одинакова). Наступает предель-

ное равновесие: в пролете образуется еще один

12/

l2

2

1

пластический шарнир, вслед за чем балка превра-

l2

2-é ýòàï

q

q

1

16=2/ 2l q

щается в механизм и разрушается.

q

=

Ðèñ. III.12.1

В итоге после перераспределения усилий, пролет-

ной свободно опертой балке М =q

l 2 / 8. Таким образом, в пределе

á

2

q

на опоре установился момент M′

2

= –q

l 2 /16, в полете M

2

= q

l 2 / 16.

2

2

l

l

Но момент на опоре на 2-ом этапе не мог возрасти. Следовательно,

M′

2

2

/ 12, откуда q2 = 16q1

/12 = 1,33 q1. В результате перерасп-

–q2l /16 = –q1l

ределения нагрузка возросла в 1,33 раза, а эпюра моментов оказа-

лась передвинутой вниз на величину M = ql 2/48, что равносильно до-

M

M

бавлению к существующей упругой эпюре еще одной эпюры M со

M

знаком «+». Эпюру M называют «добавочной».

На практике нагрузка известна заранее. Тогда пластические шар-

ниры можно использовать так: выровнять опорные M′ и пролетные

M моменты, передвинув вниз всю эпюру (рис. III.12.2). Форма доба-

вочной эпюры зависит от расчетной схемы конструкции и вариан-

тов загружения временной нагрузкой. Например, у двухпролетной

Ðèñ. III.12.2

свободно опертой неразрезной балки она будет треугольной, так как

a

X a

влияние пластического шарнира на опоре распространяется на два соседних пролета.

пряжений в арматуре, т.е. сила обжатия Р1 больше, чем при эксплуатации Р2. Например, при подъеме

преднапряженной балки после изготовления к отрицательному изгибающему моменту

a

X a

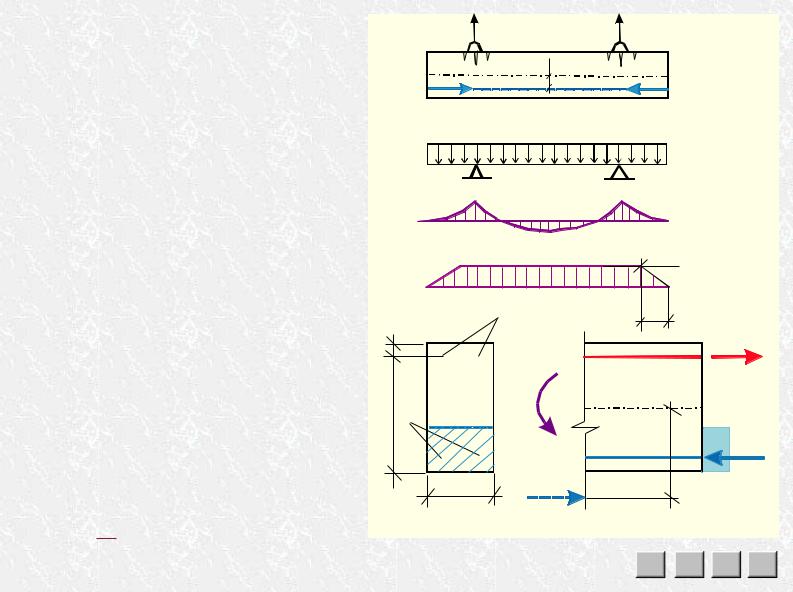
Ìð от силы обжатия Р добавляется отрица-

тельный момент Мw от собственного веса qw

(ðèñ. III.14.1). Верхняя арматура вместо сжа-

Ð1

îð

Ð1

тия испытывает растяжение, площадь ее се-

å

чения может оказаться недостаточной, на

верхней грани в местах строповки чрезмер-

но раскроются трещины, а может произойти

и разрушение по нормальному сечению.

qw

III.15. Особенности расчета в

предэксплуатационной стадии

Ìw

Сила обжатия Р1 рассматривается как вне-

шняя нагрузка: Р1 = (σsp1– 330)Àsp, ãäå

σsp1 —

Mp= Ð1åîð

величина предварительного напряжения арма-

туры с учетом первых потерь и коэффициента

точности натяжения γsp > 1; 330(ÌÏà) — âåëè-

lð

чина падения напряжений в арматуре S

p

â ìî-

S′

a′

мент разрушения сжатой зоны, соответствую-

RsAs′

щая предельной сжимаемости бетона εbu ïðè

∙

∙

кратковременном сжатии. Rb принимают по пе-

редаточной прочности Rbp с коэффициентом

′

ö.ò.

γb2 = 1,1. Нагрузку от собственного веса прини-

î

+

Ìw

мают расчетной и умножают на коэффициент

h

S

Rb

î

динамичности kd = 1,4 (при перевозке изделий

∙

∙

å

kd = 1,6), который учитывает дополнительную

RscAs

перегрузку от толчков, рывков и т. п. воздей-

b

Ð

ствий. В итоге, расчет сводится к расчету

1

нормального сечения на внецентренное сжа-

Ðèñ. III.14.1

òèå (ñì. ï. IV. 3) от действия силы Р1, прило-

+ Ìw / P1. Сечения обычных

женной относительно оси с эксцентриситетом еî = åîð

Å

a

X a

конструкций рассчитывают на изгиб, поменяв местами арматуру S и S′.

IV. 1. Работа железобетона при сжатии

При центральном сжатии бетонной призмы (рис. IV.1.1а) деформации εb в разных точках сече-

ния одинаковы, значит одинаковы и напряжения σb. При внецентрен-

à)

eî

ном сжатии деформации сечения меняются по линейному закону (по

N

N

гипотезе плоских сечений), но зависимость σb— εb криволинейна

(ñì. ï I.2), поэтому криволинейна и эпюра σb.

После центрального приложения усилия N к железобетонной приз-

ме бетон и арматура, работающие совместно, укоротятся на величи-

íó εb= εs=

1 / l (ðèñ. IV.1.1б). В бетоне установится усилие Nb1 , à â àðìà-

Ýï. ε

b

òóðå — Nsc1. Затем, вследствие ползучести, деформации вырастут на

величину 2.

Ýï. σ

b

Поскольку арматура работает практически упруго, сжимающие на-

пряжения в ней возрастут на величину

σsc= ( 2 / l)Ås, а усилие — на

Nsc=

σscAs, ãäå As — площадь сечения арматуры.

á)

N

Таким образом, в арматуре установится усилие

1

N

Nsc2 = Nsc1+

Nsc. Íî åñëè Nsc растет, а внешняя сила

2

N постоянна, то, значит, напряжения и усилие в бето-

As

не падают: N = Nb1+ Nsc1= Nb2+ Nsc2. Происходит пе-

l

рераспределение напряжений: бетон со временем

разгружается, а арматура догружается. Степень

этого перераспределения зависит от соотношения

деформативных свойств бетона и арматуры.

Nb= 0

Nb1> Nb2

Бетон — неоднородный материал, его плотность,

деформативные и прочностные характеристики ме-

Nsc= 0

N

< N

няются в определенных пределах (ñì. ï. I. 4). Èç-çà

sc1

sc2

неоднородных свойств бетона физический центр се-

Ðèñ. IV.1.1

чения не совпадает с геометрическим. Поэтому даже при идеальной центрации Å a

X a

IV.3. Расчет прочности внецентренно сжатых элементов

Из условия равновесия по моменту относительно оси арматуры S находят несущую способность

сечения (Ne)u= Nbzb+ Ns′zs, для прямоугольного сечения (Ne)u = Rbbx(ho– 0,5x) + RscAs¢(ho– a¢) (ðèñ. IV.3.1).

Условие прочности имеет вид: Ne £ (Ne)u, ãäå

′

a′

Ne — момент продольной силы N относитель-

S

N

Ns′

·

·

но оси арматуры S, для прямоугольного се-

o

x

чения е = е η + (0,5h – a), ãäå å = M /N (ñì. ï. IV.1).

e

Nb

î

î

+

s

Из суммы проекций всех сил на продольную ось

h

o

e

b

(N + Ns– Nb – Ns′ = 0) находят высоту сжатой

h

z

z

зоны x. Для прямоугольного сечения N + RsAs–

a

·

·

– Rbbx –RscAs′=0,откуда х=(N+RsAs–RscAs′)/(Rbb).

S

Ns

Åñëè õ > õR, то имеет место 2-й случай и вме-

b

ñòî Rs появляется неизвестное σs, которое за-

Ðèñ. IV.3.1

висит от высоты сжатой зоны. Тогда значения

õ è σs определяют расчетом по “общему случаю” (ñì. ï. IV.8), а для элементов из бетона класса

В30 и ниже с ненапрягаемой арматурой классов А-I, A-II, A-III — из совместного

Nu

решения уравнений: N +σsAs– RscAs′ = Rbbx è σs= (2(1 – x) / (1– xR) – 1)Rs, ãäå

ξ = 1,1

x = x / h0. Как видно из второго уравнения, при x = xR напряжения σs= Rs, à ïðè

ξ = 1

x = 1 (все сечение сжато) σs = –Rs, ò.å. σs= Rsc.

Если сечение тавровое с полкой в сжатой зоне, при х £ hf¢, расчет ведут по

тем же формулам, что и для прямоугольного сечения, заменив в них b на bf¢.

ξR

Åñëè x > hf¢, в формулы добавляется по одному слагаемому, соответственно:

Nbf = Rb(bf¢– b)hf¢ è Mbf = Nbf(ho– 0,5hf¢).

Из сказанного видно, что усилия Nu è Mu взаимозависимы. Для каждого слу-

Mu

чая можно построить диаграмму Nu— Mu: задаются значениями ξ îò 0 äî 1, îïðå-

Ðèñ. IV.3.2

деляя каждый раз (Ne)u из условия еМs= 0 è Nu из условия еN = 0 (рис. IV.3.2).

Å a

X a

В случаях, когда продольное усилие приложено только со случайным эксцентриситетом еî= åà è

гибкость элемента λ = lo

/ h ≤ 20, допускается расчитывать внецентренно сжатый элемент как условно

центрально сжатый [3].

Å a

X a

блюдая рекомендации о максимальном суммарном проценте армирования μmax£ 15%. В процессе стро-

ительства жесткая арматура воспринимает нагрузку от опалубки, свежего бетона Å a

X a