1_ЛЕКЦИИ ПО ЖБК / ЛЕКЦИИ ПО ЖБК ПГС Вторая часть / Лекция 14

Лекция № 15.

Поверхности вращения

Оболочки вращения с вертикальной осью являются старейшей формой тонкостенных пространственных покрытий.

Важнейшей разновидностью таких оболочек являются оболочки с постоянным радиусом кривизны меридиана.

К таким оболочкам принадлежат: цилиндрические и конические оболочки, радиусы кривизны меридиана которых бесконечно велики (оболочки вращения одинарной кривизны); сферические и кольцевые оболочки (оболочки вращения двоякой кривизны); круглые и кольцевые плиты, которые можно рассматривать как предельный случай конических оболочек.

Уравнение поверхности вращения с вертикальной осью

Рис. 14.1. Поверхность вращения с вертикальной осью

Большое значение для теории поверхностей вращения имеют теоремы Гульдена.

Теорема 1. Площадь поверхности вращения, заключенная между двумя параллельными кругами, равна произведению 2p на статический момент дуги меридиана, заключенной между этими кругами, относительно оси вращения

Рис. 14.2. К первой теореме Гульдена

Теорема 2. Объем тела вращения, заключенный между двумя параллельными кругами, равен произведению 2p на статический момент площади, ограниченной этими кругами и дугой меридиана, относительно оси вращения:

Рис. 14.3. Ко второй теореме Гульдена

Купола

В зависимости от очертания образующей купол может быть шаровым, коническим, эллиптическим.

Купола обладают особенно благоприятными условиями пространственной работы. По расходу материалов он экономичней других типов оболочек. Монолитные купола делают преимущественно гладкими; сборные – ребристыми.

Купола считают пологими, если отношение подъема их оболочки к диаметру в плане составляет не более

Купольное покрытие состоит из основных конструктивных элементов: оболочки купола и опорного кольца (рис. 14.4). При наличии в куполе центрального проема устраивается также верхнее кольцо, окаймляющее проем.

Рис. 14.4. Купол

Статически определимым опиранием купола является непрерывное по контуру шарнирно-подвижное опирание, совпадающее по направлению с касательной к оболочке (рис. 14.5)

Рис. 14.5. Расчетная схема купола с шарнирно-подвижным опиранием по контуру

При распределенных осесимметричных нагрузках и статически определимом опирании в тонкостенных куполах, не имеющих изломов в образующих, изгибающие моменты и и поперечные силы настолько малы, что ими можно пренебречь. Поэтому в указанных условиях тонкостенные купола могут рассчитываться по безмоментной мембранной теории.

Элемент купола, ограниченный двумя меридиональными и двумя кольцевыми сечениями, находится под воздействием усилий: меридионального Т1, кольцевого Т2 и касательного S, которые условно считают отнесенные к единицы длины сечения.

При осесимметричных нагрузках усилия S = 0, а усилия Т1 и Т2 определяют из условий статики (рис. 14.6)

Рис. 14.6. Расчетные усилия в куполе

Введем обозначения:

f – текущая угловая координата;

Q f – нагрузка на сегмент, ограниченный углом f

Тогда

Горизонтальная проекция усилия Т1 – распор – равна

Из условия равновесия элементов купола уравнение суммы проекций его внутренних усилий и нагрузки на нормаль к поверхности элемента запишется

Z – составляющая нагрузка, нормальная к поверхности купола.

Принимаем следующие обозначения

Тогда

Разделив обе части уравнения на , получим

Для шарового купола

Тогда

Обозначив нагрузку от собственного веса шарового купола на единицу поверхности g, получаем

Рис. 14.7. Расчетная схема шарового купола

Тогда

Для полушарового купола

Рис. 14.8. Эпюры усилий в полушаровом куполе от собственного веса

• Шов перехода (T2 = 0)

В реальных конструкциях оболочка купола не свободна оперта, а имеет закрепление на опорном кольце. В связи с этим на опорном контуре оболочки возникают дополнительные статически неопределимые контурные уислия – изгибающий момент М и распор Н.

Влияние упругого контурного закрепления сказывается на оболочке купола лишь вблизи кольца и накладывается на общее мембранное напряженное состояние оболочки.

Основными нагрузками, определяющие размеры конструкции купола, являются: собственный вес оболочки с утеплителем и кровлей и снеговая нагрузка. Ветровые нагрузки при пологих купольных покрытиях не принимаются во внимание.

При вспарушенных куполах усилия от ветровых нагрузок определяются приемами теории упругости.

Задача определения краевых усилий при упругом закреплении купола по контуру решена П.Л. Пастернаком в 1925 -1927 гг. и сведена к обычным уравнениям строительной механики. При решении используется теория длинной балки на упругом основании.

Рис. 14.9. Расчетная схема купола, упруго защемленного по контуру

Рис. 14.10. Усилия, возникающие в кольце

а – под влиянием радиально действующих распоров; б – под влиянием радиально действующих моментов

Армирование куполов производится в соответствие с усилиями, полученными в результате расчета (рис. 14.11).

Рис. 14.11. Армирование куполов

а – обычное армирование; б – предварительное напряжение кольцевой арматуры

1 – основная конструктивная сетка; 2 – дополнительная арматура; 3 - кольцевая арматура по расчету на Т2; 4 – рабочая арматура опорного кольца; 5 – напрягаемая арматура; 6 – торкретная штукатурка

Оболочки пологих куполов, за исключением приопорных зон, сжаты. Их армируют конструктивно – одиночной сеткой из стержней d = 5 - 6 мм с шагом 150 – 200 мм.

У контура ставят дополнительную меридиональную арматуру, рассчитанную по опорному моменту, обычно из стержней d = 6 - 8 мм и дополнительную кольцевую арматуру для восприятия местных растягивающих кольцевых усилия Т1.

Рабочую арматуру опорного кольца, рассчитываемую по центральному растяжению, ставят в виде кольцевых стержней d = 20 - 30 мм ,которые стыкуют с помощью сварки.

Также опорные кольца куполов подвергают предварительному обжатию путем натяжения кольцевой рабочей арматуры.

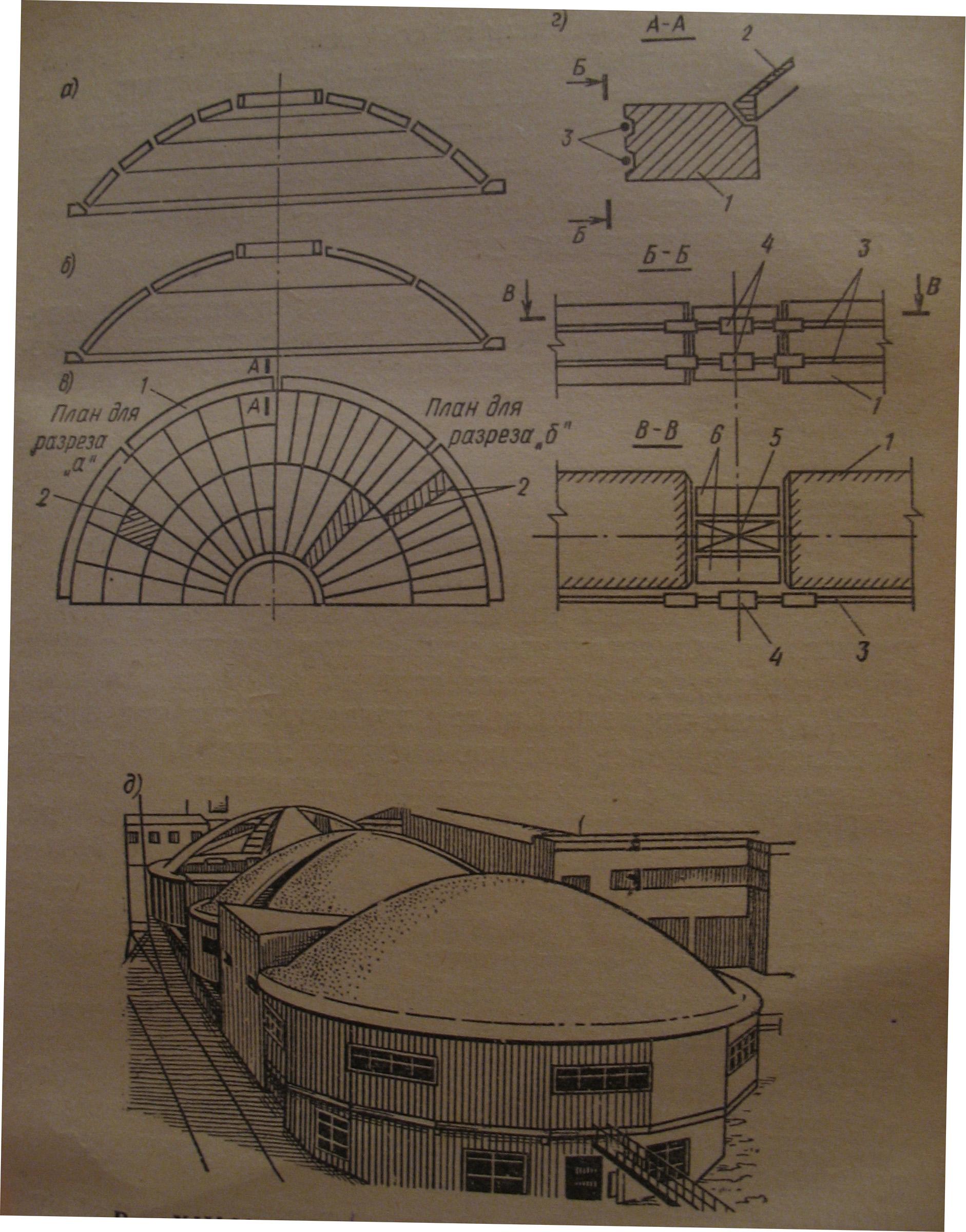
Рис. 14.12. Конструктивные схемы сборных куполов

а – разрез купола с плоскими трапециевидными элементами; б – то же с криволинейными элементами; в – разрека купола на сборные элементы; г – деталь опорного кольца; д – купольное покрытие в Караганде