
- •Новосибирский государственный
- •Оглавление
- •Введение
- •1. Система автоматического контроля
- •1.1. Функциональная схема сак
- •1.2. Классификация контрольно-измерительных приборов
- •1.3. Характеристики измерительных приборов
- •1.4. Основные элементы сак
- •1.4.1. Измерительные преобразователи (датчики)
- •1.4.2. Датчики перемещений
- •1.4.3. Датчики температуры
- •1.4.4. Датчики давления
- •1.4.5. Датчики расхода
- •1.4.6. Индукционные расходомеры
- •1.4.7. Датчики уровня
- •1.5. Методы измерений и измерительные схемы
- •1.5.1. Понятие о методах измерения
- •1.5.2. Мостовые измерительные схемы
- •1.5.3. Компенсационные измерительные схемы
- •1.5.4. Дифференциальная измерительная схема
- •2. Система автоматического управления
- •2.1. Функциональная схема сау электроприводом
- •2.2. Аппараты автоматического управления и защиты электроприводов
- •2.2.1. Командоаппараты
- •Кнопки управления
- •Путевые и конечные выключатели
- •Ртутные контакты
- •2.2.2. Реле Общие сведения и классификация реле
- •Электрические реле
- •2.2.3. Контакторы и магнитные пускатели
- •2.2.4. Аппараты защиты электроприводов
- •Реле максимального тока
- •2.3. Электрические схемы управления
- •2.3.1. Электрические схемы и их начертание
- •2.3.2. Электрическая схема управления задвижкой
- •2.3.3. Электрическая схема управления
- •2.3.4. Электрическая схема управления подпиточными насосами
- •2.3.5. Электрическая схема управления электродвигателем дымососа
- •2.3.6. Электрическая схема управления дутьевым вентилятором
- •2.3.7. Электрическая схема управления электродвигателем насоса сетевой воды
- •2.4. Электронные устройства и приборы в системах тГиВ
- •2.4.1. Общие сведения
- •2.4.2. Полупроводниковые приборы
- •2.4.3. Выпрямители
- •2.4.4. Усилители
- •2.4.5. Логические элементы
- •2.5. Микропроцессорные системы
- •2.6. Микропроцессорное управление электроприводами
- •3. Система автоматического регулирования
- •3.1. Понятие об автоматическом регулировании.
- •3.2. Основные свойства объектов регулирования
- •3.3. Динамические звенья сар
- •3.4. Типовые звенья сар и их характеристики
- •3.5. Структурная схема сар
- •3.6. Устойчивость линейных сар
- •3.7. Оценка качества регулирования линейных систем
- •3.8. Автоматические регуляторы
- •3.8.1. Классификация и законы регулирования
- •3.8.2. Выбор типа регулятора
- •Заключение
- •Библиографический список
3.4. Типовые звенья сар и их характеристики
Типовыми динамическими звеньями называются звенья, описываемые дифференциальными уравнениями не выше второго порядка.
Основными типовыми звеньями являются: пропорциональное, апериодическое, колебательное, дифференцирующее, интегрирующее и звено с чистым запаздыванием.
Звенья обладают направленным действием. Это значит, что сигнал через звено может проходить только в одном направлении – от входа к выходу. Любые изменения выходной величины звена не отражаются на его входной величине. Это позволяет рассматривать каждое звено отдельно, независимо от других звеньев.
Пропорциональное звено. Пропорциональным называется звено, у которого в каждый момент времени выходная величина пропорциональна входной величине.
Уравнение переходного процесса звена
![]() ,
(3.15)
,
(3.15)
где
![]() – коэффициент усиления (передачи) звена.
– коэффициент усиления (передачи) звена.
Переходная характеристика пропорционального звена представлена на рис. 3.12.
Рис. 3.12. Переходная характеристика пропорционального звена
При
подаче на вход пропорционального звена
ступенчатого сигнала
![]() соответствующее значение выходной
величины
соответствующее значение выходной
величины![]() устанавливается мгновенно.
устанавливается мгновенно.
Передаточная функция звена
![]() .
(3.16)
.
(3.16)
Примером пропорционального звена может быть реостатный датчик, транзистор, работающий в режиме усиления, безлюфтовая зубчатая передача и др.
Апериодическое звено. Апериодическим (или инерционным) называется звено, в котором при скачкообразном (ступенчатом) изменении входной величины выходная величина стремится апериодически (по закону экспоненты) к новому установившемуся значению.
Уравнение переходного процесса апериодического звена
![]() ,
(3.17)
,
(3.17)
где
![]() –
постоянная времени звена;
–
постоянная времени звена;![]() –
коэффициент передачи.
–
коэффициент передачи.
Решение уравнения (3.17) имеет вид
![]() ,
(3.18)
,
(3.18)
где
![]() –
основание натурального логарифма.
–
основание натурального логарифма.
Переходная характеристика апериодического звена представлена на рис. 3.13.
Р ис.
3.13. Переходная характеристика
апериодического звена
ис.
3.13. Переходная характеристика
апериодического звена
Величина
![]() может
быть найдена как проекция касательной
на линию установившегося значения.
Кроме того,
может
быть найдена как проекция касательной
на линию установившегося значения.
Кроме того,![]() можно
найти из свойства, что в момент времени
можно
найти из свойства, что в момент времени![]() переменная
переменная![]() должна иметь
должна иметь![]() значение
значение
![]() (3.19)
(3.19)
Для
большинства практических случаев можно
считать, что переходный процесс в
апериодическом звене заканчивается к
моменту времени
![]() .
.
Передаточную функцию апериодического звена можно получить из выражения (3.5)
![]() .
(3.20)
.
(3.20)
К апериодическим звеньям можно отнести большинство тепловых объектов, термопары, термометры сопротивления, магнитные усилители, электрические цепи с элементами R и L, R и С.
Колебательное звено. Колебательным называется звено, в котором при подаче на вход ступенчатого воздействия выходная величина стремится к установившемуся значению, совершая затухающие колебания.
Колебательное звено иначе называют двухъемкостным, т.е. оно должно содержать два элемента, способных запасать энергию или вещество и обмениваться этими запасами через третий элемент.
Дифференциальное уравнение колебательного звена:
![]() (3.21)
(3.21)
или в операторной форме
![]()
![]() ,
(3.22)
,
(3.22)
где
![]() – постоянная времени, характеризующая
демпфирование (затухание) собственных
колебаний звена;
– постоянная времени, характеризующая
демпфирование (затухание) собственных
колебаний звена;![]() –
постоянная времени, характеризующая
раскачивание собственных колебаний
звена;
–
постоянная времени, характеризующая
раскачивание собственных колебаний
звена;![]() –
коэффициент усиления.
–
коэффициент усиления.
Переходная характеристика колебательного звена представлена на рис. 3.14.
Следует иметь в виду, что не всякое уравнение второго порядка (3.21) выражает колебательный процесс.
Если
![]() ,
то практически будет иметь место
апериодический процесс (кривая2).
При таких параметрах
,
то практически будет иметь место
апериодический процесс (кривая2).
При таких параметрах
![]() и
и![]() динамическое звено
динамическое звено![]() называют
апериодическим звеном второго порядка.
называют
апериодическим звеном второго порядка.
Если
![]() ,
то будет иметь место колебательный
процесс (кривая 1). Чем меньше отношение
,
то будет иметь место колебательный
процесс (кривая 1). Чем меньше отношение![]() ,
тем сильнее проявляются колебания.
,
тем сильнее проявляются колебания.
Решение дифференциального уравнения для колебательного звена:
![]() ,
(3.23)
,
(3.23)
где
![]() –
постоянная времени, характеризующая
длительность переходного процесса.
–
постоянная времени, характеризующая
длительность переходного процесса.
Величина
![]() может
быть определена графически по кривой
(рис. 3.14), как постоянная времени огибающей
экспоненты.
может
быть определена графически по кривой
(рис. 3.14), как постоянная времени огибающей
экспоненты.

Рис. 3.14. Переходная характеристика колебательного звена
Аналитически
величину
![]() можно
определить по формуле
можно
определить по формуле
![]() ;
;
![]() .
(3.24)
.
(3.24)
Постоянные
времени
![]() и
и![]() часто определяют по параметрам элементов
колебательного звена.
часто определяют по параметрам элементов
колебательного звена.
Частота собственных колебаний звена
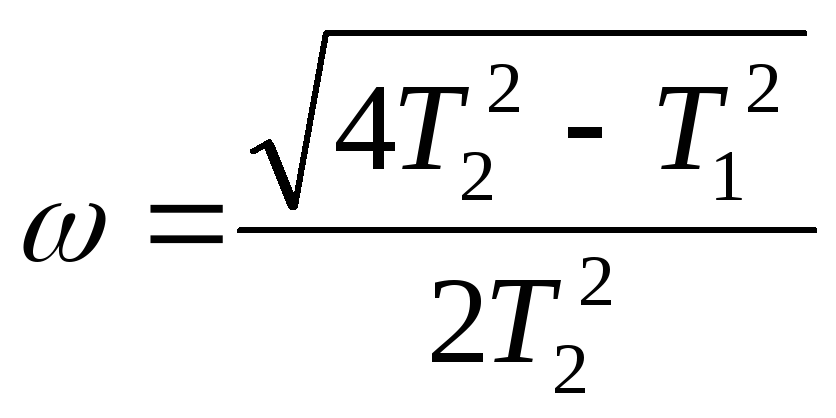 .
(3.25)
.
(3.25)
Передаточная функция колебательного звена
![]() .
(3.26)
.
(3.26)
К колебательным звеньям относятся:
– электрическая цепь с последовательным соединением R, L и C;
– сообщающиеся сосуды;
– электродвигатели, способные запасать кинетическую энергию в якоре и электромагнитную в якорной цепи;
– механические
элементы, обладающие массой, упругостью
и вязким трением и др.![]()
Например,
для электрической цепи с последовательным
соединением параметров R,
L
и C
(рис. 3.15), постоянные времени
![]() и
и![]() можно определить по формулам:
можно определить по формулам:

![]()
![]() .
(3.27)
.
(3.27)
Рис. 3.15. Электрическая цепь с последовательным
соединением параметров R, L и C
Дифференцирующее звено. Это звено, у которого выходная величина пропорциональна скорости изменения входной величины. Как всякое реальное звено, дифференцирующее звено имеет инерционные свойства.
Дифференциальное уравнение звена (реального):
![]() .
(3.28)
.
(3.28)
Его решение
![]() ,
(3.29)
,
(3.29)
где
![]() –
постоянная времени звена;
–
постоянная времени звена;![]() –
коэффициент передачи.
–
коэффициент передачи.
Переходный процесс в дифференцирующем звене представлен на рис. 3.16.
Если
инерционные свойства звена незначительны
в сравнении с другими звеньями САР, то
величину
![]() опускают
и получают уравнение идеального
дифференцирующего звена
опускают
и получают уравнение идеального
дифференцирующего звена
![]() .
(3.30)
.
(3.30)
Передаточная функция реального звена:
![]() ,
(3.31)
,
(3.31)
а идеального звена
![]() .
(3.32)
.
(3.32)
К
дифференцирующим звеньям относятся:
тахогенератор (датчик скорости), у
которого
![]() – угол поворота вала, а
– угол поворота вала, а![]() – напряжение; пневматические и
гидравлические успокоители; дифференцирующий
трансформатор; цепь, состоящая из
элементовR
и C.
– напряжение; пневматические и
гидравлические успокоители; дифференцирующий
трансформатор; цепь, состоящая из
элементовR
и C.
Дифференцирующие звенья находят широкое применение как составные элементы корректирующих устройств САР.
Р ис.
3.16. Переходная характеристика
дифференцирующего звена
ис.
3.16. Переходная характеристика
дифференцирующего звена
Интегрирующее звено. Это звено, у которого скорость изменения выходной величины пропорциональна входной величине.
Уравнение идеального интегрирующего звена
![]() .
(3.33)
.
(3.33)
Уравнение интегрирующего звена с учетом инерционных свойств
![]()
![]() .
(3.34)
.
(3.34)
Переходная характеристика интегрирующего звена представлена на рис. 3.17.
Р ис.
3.17. Переходная характеристика
интегрирующего звена
ис.
3.17. Переходная характеристика
интегрирующего звена
Передаточные функции:
– идеального
звена
![]() ;
(3.35)
;
(3.35)
– звена
с инерцией
![]() , (3.36) гдеk
- угловой
коэффициент наклона касательной к оси
абсцисс.
, (3.36) гдеk
- угловой
коэффициент наклона касательной к оси
абсцисс.
Примерами
интегрирующего звена являются: поршневой
ИМ, у которого входная величина –
перемещение плунжера золотникового
устройства, а выходная – перемещение
силового поршня; маломощный асинхронный
двигатель с полым ротором; контур R
– C,
если
![]() и др.
и др.
Звено
с чистым запаздыванием.
У звена с чистым запаздыванием выходная
величина воспроизводит без искажения
все изменения входной величины с
некоторым постоянным запаздыванием
![]() (рис. 3.18).
(рис. 3.18).
У равнение
звена с чистым запаздыванием
равнение
звена с чистым запаздыванием
![]() ,
(3.37)
,
(3.37)
где
![]() – время запаздывания.
– время запаздывания.
Передаточная функция звена
W(p) = e– τ· p. (3.38)
Примеры запаздывающего звена: транспортер, подающий груз от бункера к весам; трубопровод гидросистемы; длинные воздуховоды; реле, работающие в режиме усиления и др.

Рис. 3.18. Переходная характеристика звена с чистым запаздыванием
Способы соединения звеньев САР. Существует три основных типа соединения динамических звеньев: последовательное, параллельное и встречно-параллельное (или соединение с обратной связью) (рис. 3.19).
Приведенные передаточные функции соединений звеньев САР широко применяются для получения передаточной функции всей системы регулирования, которая в дальнейшем является исходной для оценки устойчивости и качества САР.
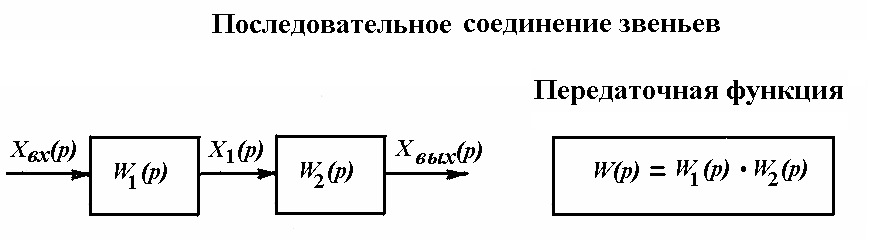
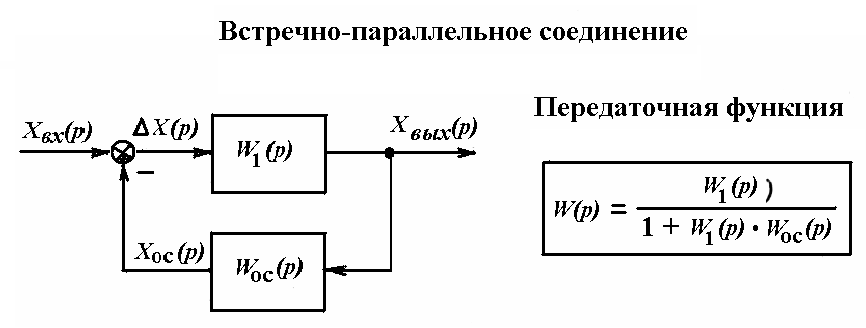
Рис. 3.19. Способы соединения звеньев САР
